随机森林算法原理
文章目录
- 熵值法介绍
- 熵值法公式的理解
- 决策树的原理及Python实现
- bagging的原理
- 最小二乘回归树算法实现
- 一个简单的最小二乘预测器
- 线性回归器简单示例
熵值法介绍
熵定义:熵值法是计算指标权重的经典算法之一,它是指用来判断某个指标的离散程度的数学方法。其和化学里面的概念是相同的,指物体内部的混乱程度。混乱程度(纯度)低则熵值小,反之!
查看了很多文献,好像对熵值的解读都很高深,现在说下自己的理解
熵值法公式的理解
熵值公式链接
决策树与随机森林学习笔记
为什么要用-p*log('p)这个公式?
这个问题先放下,看看下面这些问题
假设我们用了一个只能装8个分子的盒子装了8个分子,当容器中存在空隙时分子会任意乱飞,系统的熵值本来就是表示物体内部的混乱程度的,这时我们可以用公式可以求出系统的总熵值为0( 0和log函数相乘无限趋近于0时值为0),同理当盒子中没有分子时总熵值也为0
这时我们考虑两个系统,一个容积为4个分子的器皿装了2个分子,和一个容积为8个分子的器皿装了4个分子,他们的熵值是不是相同,当然一样。他们的总熵值都为1,也就是他们都处于最极端混乱的状态。
注:容积为8的器皿装5个分子和装3个分子,他们的混乱状态相同
同一个系统中,熵值是满足相加性的,熵值只是一个相对属性,不要把不同系统的熵值搞混
问什么要用-p*log('p)这公式?因为他满足以下条件,自己可以试着去掉一些参数看看它满不满足,熵值公式必须满足了系统以下几个特征:
1:连续性
该量度应连续,概率值小幅变化只能引起熵的微小变化
2:对称性
符号xi重新排序后,该量度应不变,这也是我们可以归一化、标准化矩阵参数的原因,因为无论怎么变,行向量的混乱程度的都不会变
3:可加性
熵的量与该过程如何被划分无关
4:极值性
当所有符号有同等机会出现的情况下,熵达到最大值(所有可能的事件同等概率时不确定性最高)
熵值算法的例子
上面链接中的大神已经为我们做了详细解释,我简单对熵值算法坐下解释:
我们对比整个表的第一列,可以看出第一列有3个属性:
| index | age | buys_computer |
|---|---|---|
| 0 | [youth,youth,youth,youth,youth] | [yes,yes,no,no,no] |
| 1 | [middle,middle,middle,middle] | [yes,yes,yes,yes] |
| 2 | [senior,senior,senior,senior,senior] | [yes,yes,yes,no,no] |
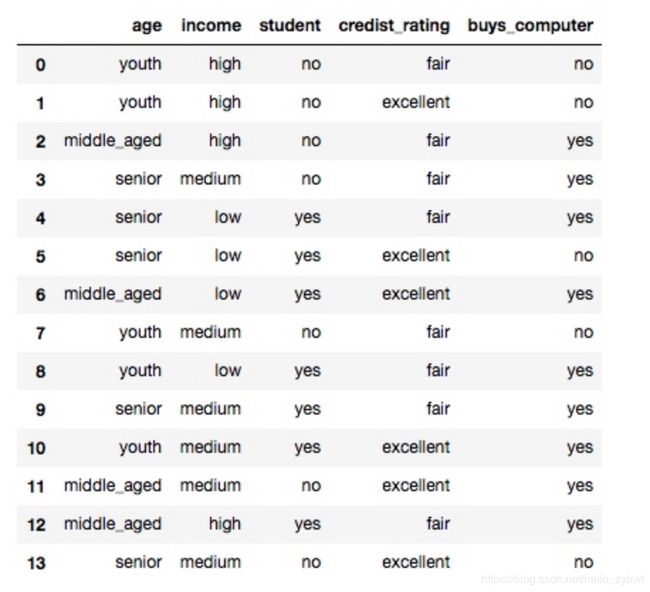
我们完全不用看buys_computer的排序,我们可以把age看成一个由3个箱子组成,分别装了[2,4,3]个分子的盒子,最后合并成一个箱子的系统
系统一开始的熵值:
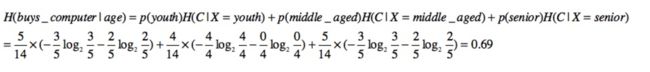
最后合并成一个系统后的熵值:
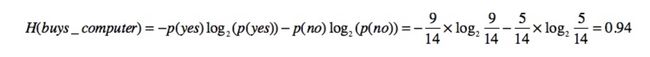
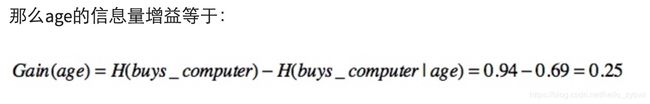
其余列的增益可以从链接文档中查看。
简而言之系统的状态变化越大,熵值变化量越大,代表列越复杂,它所包含的信息量也越多,它对输出结果的影响也越大,它在决策树中的层级也就越高。
决策树的原理及Python实现
决策树的原理和实现链接1
决策树的原理和实现链接2
bagging的原理
集成学习有两个流派,一个是boosting派系,它的特点是各个弱学习器之间有依赖关系。另一种是bagging流派,它的特点是各个弱学习器之间没有依赖关系,可以并行拟合从下图可以看出,Bagging的弱学习器之间确没有boosting那样的联系。它的特点在于“随机采样”。那么什么是随机采样?
随机采样(bootsrap)就是从我们的训练集里面采集固定个数的样本,但是每采集一个样本后,都将样本放回。也就是说,之前采集到的样本在放回后有可能继续被采集到。对于我们的Bagging算法,一般会随机采集和训练集样本数m一样个数的样本。这样得到的采样集和训练集样本的个数相同,但是样本内容不同。如果我们对有m个样本训练集做T次的随机采样,则由于随机性,T个采样集各不相同。
注意到这和GBDT的子采样是不同的。GBDT的子采样是无放回采样,而Bagging的子采样是放回采样。
对于一个样本,它在某一次含m个样本的训练集的随机采样中,每次被采集到的概率是1/m。不被采集到的概率为1/m−1。如果m次采样都没有被采集中的概率是(1−1/m)^m
当m→∞时,(1−1/m)^m→1e≃0.368。也就是说,在bagging的每轮随机采样中,训练集中大约有36.8%的数据没有被采样集采集中。
对于这部分大约36.8%的没有被采样到的数据,我们常常称之为袋外数据(Out Of Bag, 简称OOB)。这些数据没有参与训练集模型的拟合,因此可以用来检测模型的泛化能力。
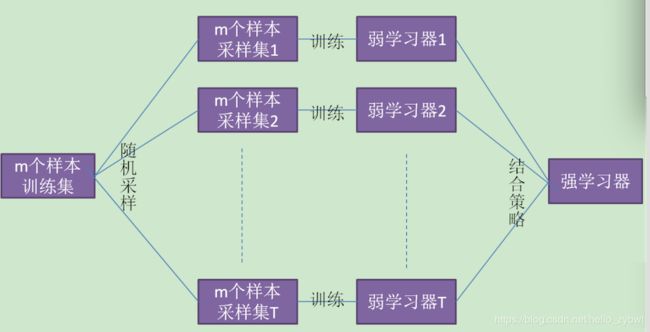
最小二乘回归树算法实现
一个简单的最小二乘预测器
我们拿上面图一的简单方程说起,我们构造2组数据:
两个方程参数分别接近(1,2,3,4,5),(1,2,2,4,5)
我们可以自己动手加下,只有最后一组数据有些许偏差(16—>15, 15---->14)
X1 = np.array([[-2,-1,0,1,2],[-1,0,1,2,3],[1,1,1,0,0],[1,1,0,1,0],[1,0,0,0,1],[1,1,1,1,1]])
X2 = np.array([[1,0,0,2,1],[-1,0,2,1,1],[-3,1,2,0,0],[-4,2,0,1,1],[1,1,0,0,0],[1,1,1,1,1]])
Y1 = np.array([[10],[25],[6],[7],[6],[16]])
Y2 = np.array([[14],[12],[3],[9],[3],[15]])
X = np.vstack((X1,X2))
Y = np.vstack((Y1,Y2))
这时我们可以得到两个2维(我们用几个下标可以把X表示出来,可以用X.ndim算出) 简单方程,2*6组数据5个系数:
class Least_square:
def __init__(self):
self.param = np.array([])
self.Y = np.array([])
def fit(self, X, Y):
X_T = X.transpose()
self.param = np.dot(np.dot(np.linalg.inv(np.dot(X_T,X)),X_T),Y)
self.Y = Y
return self.param
def predict(self,X):
result = np.dot(X,self.param)
var = np.var(self.Y - result)
return result, var
least_instance = Least_square()
param = least_instance.fit(X,Y)
result,var = least_instance.predict(X)
线性回归器简单示例
from sklearn.linear_model import LinearRegression
regression = LinearRegression()
param = regression.fit(X, Y)
score = regression.score(X,Y)
result = regression.predict(X)
