统计学基础——方差、协方差、标准差（标准偏差/均方差）、标准误、均方误差、均方根误差(标准误差)的区别
方差（Variance)
概率论
离散型随机变量的数学期望： 
，其中，
是变量
发生的概率。
连续型随机变量的数学期望：
，其中，f(x)是概率密度。
方差值：![D(X)=Var(X)=E[X-E(X)]^{2}=E(X)^{2}-[E(X)]^{2}](http://img.e-com-net.com/image/info8/e55fcf2cf89541ac8c6856a1643676b7.gif){kind=small}
，证明过程：
假设：
，则
,则
统计学
总体方差，也叫做有偏估计，其实就是我们从初高中就学到的那个标准定义的方差：
，其中，
为总体的均值，
为总体的标准差，
为总体的样本数。
样本方差，无偏方差，在实际情况中，总体均值
是很难得到的，往往通过抽样来计算，于是有样本方差，计算公式如下：
或者
，其中，
为样本的均值，
为样本的标准差，
为样本的个数。
此处，为什么要将分母由n变成n-1，主要是为了实现无偏估计减小误差，具体原理及推导公式可上网查阅，资料很多。
协方差（Covariance）
协方差在概率论和统计学中用于衡量两个变量的总体误差。而方差是协方差的一种特殊情况，即当两个变量是相同的情况。协方差表示的是两个变量的总体的误差，这与只表示一个变量误差的方差不同。 如果两个变量的变化趋势一致，也就是说如果其中一个大于自身的期望值，另外一个也大于自身的期望值，那么两个变量之间的协方差就是正值。 如果两个变量的变化趋势相反，即其中一个大于自身的期望值，另外一个却小于自身的期望值，那么两个变量之间的协方差就是负值。
其中，
与
分别为两个实数随机变量
与
的数学期望，
为，的协方差。
标准差（Standard Deviation)
标准差也被称为标准偏差,在中文环境中又常称均方差，是数据偏离均值的平方和平均后的方根，用σ表示。标准差是方差的算术平方根。标准差能反映一个数据集的离散程度，只是由于方差出现了平方项造成量纲的倍数变化，无法直观反映出偏离程度，于是出现了标准差，标准偏差越小，这些值偏离平均值就越少，反之亦然。
总体方差
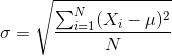，其中， 为总体的均值， 为总体的标准差， 为总体的样本数。
样本方差
，其中， 为样本的均值， 为样本的标准差， 为样本的个数。
标准误（Standard error of mean,SEM或SE)
样本均值的标准误
由固然存在的个体变异和抽样造成的不同样本均数之间的差异、样本均数与总体均数之间的差异称为均数的抽样误差（也称标准误），用于反映我们用样本均数估计总体均数有多大的误差。
若随机变量均数为，方差为
，则样本均数的标准差（标准误）为：
。又根据正态分布原理，若随机变量
，则样本均数
。
实际应用中，总体标准差通常未知，需要用样本标准差来估计标准误。此时，均数标准误的估计值为：
标准误的大小与原变量的标准差成正比，与样本含量的平方根成反比，因此，实际应用中可通过增加样本含量来减少均数的标准误，从而降低抽样误差。
例：2000年某研究所随机调查某地健康成年男子27人，得到血红蛋白的均数为125g/L，标准差为15g/L。试估计该样均数的抽样误差。
注意：标准差描述的是度量值的变化，在此题中，标准差为15g/L，标准误描述的是估计值的变化，在此题中，标准误为2.89g/L，随着样本量n的增加，标准误是会减小的，但是标准差是不变的。
样本频率的标准误
从同一总体中随机抽出观察单位相等的多个样本，样本率与总体率及各样本率之间都存在差异，称为频率的抽样误差。表示样本频率抽样误差大小的指标即为频率的标准误。
根据二项分布原理，若随机变量
，则样本频率
的总体概率为
，标准误为
。
频率的标准误愈小，用样本频率估计总体概率的可靠性愈好；反之，用样本频率估计总体概率的可靠性愈差。
实际应用中，总体概率通常未知，需要用样本频率
来近似的代替。得到频率标准误的估计值为：
频率的标准误与样本含量的平方根成反比，因此，增加样本含量可以减少样本频率的抽样误差（标准误）。
例：某市随机调查了50岁以上的中老年妇女776人，其中患有骨质酥松症者322人，患病率为41.5%，试计算该样本频率的抽样误差。
总体标准误的估计值较小，说明用样本患病率41.5%来估计患病率的可靠性较好。
均方误差（mean-square error, MSE）
均方误差是反映估计量与被估计量之间差异程度的一种度量，换句话说，参数估计值与参数真值之差的平方的期望值。MSE可以评价数据的变化程度，MSE的值越小，说明预测模型描述实验数据具有更好的精确度。
,其中
表示估计量，
表示被估计量。
均方根误差（root mean squared error，RMSE）
均方根误差亦称标准误差，是均方误差的算术平方根。换句话说，是观测值与真值(或模拟值)偏差(而不是观测值与其平均值之间的偏差)的平方与观测次数n比值的平方根，在实际测量中，观测次数n总是有限的，真值只能用最可信赖（最佳）值来代替。标准误差对一组测量中的特大或特小误差反映非常敏感，所以，标准误差能够很好地反映出测量的精密度。这正是标准误差在工程测量中广泛被采用的原因。因此，标准差是用来衡量一组数自身的离散程度，而均方根误差是用来衡量观测值同真值之间的偏差。