cs224n学习笔记 2
1 Word Meaning
需要掌握的主要是词的表示方法,大体来说,词的表示主要有下面两种:
1.1 discrete representation
用一个one-hot向量来表示一个词,比如现在有三个词apple,banana,orange分别对应向量的每个位置,那么[0,1,0]表示banana。
这种表示被称作是一种本地表示(localist representation)
当全部单词比较多的时候,discrete representation需要用比较大的维度表示一个单词,这样得到的向量是一个稀疏的向量(只有一维是1),而事实上我们希望如果两个词语词义相近,那么他们向量的内积比较大,但是用discrete representation表示两个近义词的话,他们对应的向量内积是0,这是我们不希望的
1.2 distributed representation
这种表示方法是想要用一个稠密的向量来表示一个单词,而稠密向量的维度可以不用像上一种那么大,同时我们希望两个近义词用distributed representation时对应向量的内积尽量大
关键是怎么得到这个稠密向量呢?笼统的说,我们是通过单词所处的上下文来得到的。一个单词所在文章的上下文能够体现这个单词的词义,我们称之为distributional similarity,举个例子,hotel和motel这两个单词上下文的环境一般是比较类似的。注意区分distributional similarity和我们说的distributed representation两者不是一回事,distributional similarity是语言学上表示词义的一种方式,而distributed representation是用数值(向量)的方式呈现词的一种方法。
至于具体怎么通过上下文得到稠密向量,就是下面word2vec的主要内容
2 word2vec introduction
word2vec就是为了实现distributed representation,但在细节上又有一点变化
2.1 中心词和上下文
word2vec中用两个稠密向量来表示一个单词,其中,用![]() 表示这个词作为中心词时对应的向量,用
表示这个词作为中心词时对应的向量,用![]() 表示这个词作为上下文时对应的向量
表示这个词作为上下文时对应的向量
那么什么是中心词和上下文呢?中心词和上下文是一对相对的概念,比如我有一句话 Here is the explanation for word2vec,那么当我选择explanation作为中心词的时候,here,is,the,for,word2vec就都被称为上下文。
2.2 SG与CBOW
现在我要想办法得到每一个词的![]() 和
和![]() ,主要有两种算法:
,主要有两种算法:
第一种是skip-grams(SG)算法,这种算法是假定中心词确定的情况下,得到每个词的![]() 和
和![]() ;
;
第二种是Continuous Bag of Words(CBOW)算法,这种算法是假定上下文确定的情况下,得到每个词的![]() 和
和![]()
2.3 skip-grams算法铺垫部分
第二课中,主要介绍的是skip-grams算法
skip-grams算法中有一个半径是m的滑动窗口,对于一个中心词,只有滑动窗口中中心词前后的词才被我们称为上下文。举个例子,对一句话Here is the explanation for word2vec which is a basic concept in NLP,我们滑动窗口的半径如果是2,那么窗口的大小就是2m+1(等于5),初始时,窗口中内容是[Here is the explanation for],此时中心词时the,那么除了the以外的四个词都被认为是the的上下文;窗口滑动一次,内容变为[is the explanation for word2vec],此时中心词变为explanation......依次类推,每次向后滑动一下直至滑到底。
对于当前的窗口,假设是[is the explanation for word2vec],我们前面提到过SG算法的前提是认为中心词是确定的,也就是我们已知中心词是explanation,我们希望explanation的上下文中出现is,the,for,word2vec这件事是“合理”的,我们给出一个“合理”与否的判断标准:
这个值表示确定![]() 为中心词时上下文为
为中心词时上下文为![]() 的概率,其中
的概率,其中![]() 表示中心词,在例子中就是explanation,
表示中心词,在例子中就是explanation,![]() 表示中心词的前一个词,例子中是the,
表示中心词的前一个词,例子中是the,![]() 表示中心词的后两个词,例子中是word2vec。现在我们要做的就是让这个概率最大
表示中心词的后两个词,例子中是word2vec。现在我们要做的就是让这个概率最大
2.4 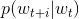 求法与softmax公式
求法与softmax公式
2.4.1 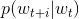 求法
求法
通过2.3,我们了解了一个窗口内的优化的目标,那么现在问题就是![]() 怎么表示的问题了
怎么表示的问题了
首先,在![]() 为中心词的前提下
为中心词的前提下![]() 出现的概率如果比较大,则说明
出现的概率如果比较大,则说明![]() 和
和![]() 这两个单词比较“亲近”(现在为了方便表示,我用o表示
这两个单词比较“亲近”(现在为了方便表示,我用o表示![]() ,用c表示
,用c表示![]() )。如果用数学语言来表示,就是c作为中心词时的向量
)。如果用数学语言来表示,就是c作为中心词时的向量![]() 与o作为上下文时的向量
与o作为上下文时的向量![]() 二者的内积
二者的内积![]() 的值越大,这两个词越“亲近”
的值越大,这两个词越“亲近”
2.4.2 softmax公式
但是,我并不能![]() 来作为
来作为![]() 的值,因为这个内积值都不一定在0到1之间,用它来做概率显然不合理
的值,因为这个内积值都不一定在0到1之间,用它来做概率显然不合理
在这里,我们用softmax公式来得到![]() 的值。为了不过分偏移主题,我们这里不具体分析softmax公式本身的优点与合理性,只给出在这个问题里softmax的形式,关于softmax的详细知识可以单独查找学习。
的值。为了不过分偏移主题,我们这里不具体分析softmax公式本身的优点与合理性,只给出在这个问题里softmax的形式,关于softmax的详细知识可以单独查找学习。
下面给出![]() 的表示:
的表示:
其中,V是语料库中所有单词的数量,我们把整个语料库中的每一个单词,都用他作为上下文的向量![]() 和
和![]() 做点积,作为这个单词和当前中心词c相似度的一个分数,把这个分数作为e的指数之后,可以认为仍然还是一个分数,只是放大或缩小了,但相对大小不变,我们希望
做点积,作为这个单词和当前中心词c相似度的一个分数,把这个分数作为e的指数之后,可以认为仍然还是一个分数,只是放大或缩小了,但相对大小不变,我们希望![]() 大,其实是希望o作为上下文时这个分数占得比重尽量大
大,其实是希望o作为上下文时这个分数占得比重尽量大
2.5 skip-grams总述
2.5.1 优化目标
2.3 2.4两节我们已经铺垫了对于一个滑动窗口内![]() 是怎么计算的;但是对于一段文字,我们希望的不仅仅是某一个滑动窗口内的概率最大,而是所有窗口中的情况同时成立时的值最大,也就是所有滑动窗口中对应概率之积最大,这个积记为
是怎么计算的;但是对于一段文字,我们希望的不仅仅是某一个滑动窗口内的概率最大,而是所有窗口中的情况同时成立时的值最大,也就是所有滑动窗口中对应概率之积最大,这个积记为![]() ,表示为
,表示为
其中T为文本中可以作为中心词的词的数量,![]() 表示所有的参数(具体来说,就是所有单词的
表示所有的参数(具体来说,就是所有单词的![]() 和
和![]() )
)
我们要调整![]() 使对应的
使对应的![]() 最大,但为了方便优化,我们更希望优化对象是一个和的形式,我们对
最大,但为了方便优化,我们更希望优化对象是一个和的形式,我们对![]() 取log,因为log函数单调递增,所以原先较大的值取log之后依然较大,现在变成了我们希望调整参数使取log之后的结果尽量大;接下来,我们在对取log之后的结果乘
取log,因为log函数单调递增,所以原先较大的值取log之后依然较大,现在变成了我们希望调整参数使取log之后的结果尽量大;接下来,我们在对取log之后的结果乘![]() ,那么就变成了我们希望当前的结果尽量小,最终要优化的函数是
,那么就变成了我们希望当前的结果尽量小,最终要优化的函数是
我们要让这个函数最小
2.5.2 skip-grams整体流程
下面用V表示所有单词的总数,d表示稠密向量的维数
(1)输入一个单词对应的one-hot向量![]() ,这个向量是V*1维的,我们假设其第m列为1
,这个向量是V*1维的,我们假设其第m列为1
(2)定义一个d*V维的矩阵![]() ,这个矩阵的第j列就是第j个单词的
,这个矩阵的第j列就是第j个单词的![]() ,所以
,所以![]() 乘
乘![]() 得到的就是输入单词作为中心词的
得到的就是输入单词作为中心词的![]() (因为
(因为![]() 只有第m维是1,所以
只有第m维是1,所以![]() 也只有那m列起作用)
也只有那m列起作用)
(3)定义一个V*d维的矩阵![]() ,这个矩阵的第i行就是第i个单词的
,这个矩阵的第i行就是第i个单词的![]() ,所以
,所以![]() 乘
乘![]() 得到一个V*1维向量
得到一个V*1维向量![]() ,其中第k维的数值就是输入的单词作为中心词时,第k个单词作为上下文时二者向量的点积
,其中第k维的数值就是输入的单词作为中心词时,第k个单词作为上下文时二者向量的点积![]()
(4)对向量![]() 进行softmax操作,得到softmax之后的向量
进行softmax操作,得到softmax之后的向量![]() ,利用它与每一个上下文单词对应的one-hot向量进行loss计算,然后反向传播,先后修改矩阵
,利用它与每一个上下文单词对应的one-hot向量进行loss计算,然后反向传播,先后修改矩阵![]() 和
和![]() ,也就是更新了每个单词对应的
,也就是更新了每个单词对应的![]() 和
和![]() ;
;
注意,这里loss计算并不是用什么square-loss之类的,其实这个loss计算还需要一部分网络,目的是用![]() 凑出
凑出![]() ,但这部分在下面的图中没有画出来,因为画出来会显得太冗长,有点喧宾夺主
,但这部分在下面的图中没有画出来,因为画出来会显得太冗长,有点喧宾夺主
具体流程可以参考课件上这张图:
3 Derivations of gradient
上一节中,我们已经搞清楚了skip-grams的整体流程还有网络结构;可是如果我们想要实现这个网络,不能忽视的一点就是反向传播过程中需要的梯度值具体是多少,下面就是推导反向传播过程中的梯度值。
3.1 矩阵求导
第一点,过去接触的求导基本上都是元素对元素求导的情况,但是实际上,矩阵、列向量、行向量、元素之间的4*4种求导方式都是存在的,他们依照的规则参见这个文档:http://files.cnblogs.com/files/leoleo/matrix_rules.pdf
第二点,这4*4种求导方式均是遵守导数的链式法则的,比如![]() 是一个矩阵,
是一个矩阵,![]() 是一个列向量,
是一个列向量,![]() 是一个元素,
是一个元素,![]() 依然成立
依然成立
记住以上两点,就能够应付求梯度时遇到的大部分情况了
3.2 SG的梯度推导
课上只给出了![]() 对
对![]() 求导得到的梯度,这个梯度是用于更新所有
求导得到的梯度,这个梯度是用于更新所有![]() 组成的矩阵
组成的矩阵![]() 的;课上没有给出
的;课上没有给出![]() 对所有
对所有![]() 求导得到的梯度
求导得到的梯度
我们把求和符号后面的内容看作一个函数![]() ,把这个函数求梯度的结果累加就是对
,把这个函数求梯度的结果累加就是对![]() 求梯度的结果,我们已知
求梯度的结果,我们已知
现在我们要求的是![]()
减号前后两部分我们依次进行求解,首先推导f1的结果:
其中最后一步变换是元素对列向量求导,得到的也是一个列向量,实际推导过程中可以先考虑这个列向量第i维的值是多少,也就是![]() 对
对![]() 求导的结果,最后再以向量的形式把结果归纳起来
求导的结果,最后再以向量的形式把结果归纳起来
下面再推导![]() 的结果:
的结果:
其中第一步变换使用了链式法则,注意把第二个求和的记号从w换成了x,这是为了和第一次求和时的符号不一样
这样一来,![]() 的梯度就求出来了,直接用公式里包含的这些值就可以完成一次反向传播时的更新
的梯度就求出来了,直接用公式里包含的这些值就可以完成一次反向传播时的更新
以上就完成了梯度的推导,但如果我们再对![]() 进行一次变化,能得到一个能够说明结果正确性的公式
进行一次变化,能得到一个能够说明结果正确性的公式
而根据概率论的知识, 正是
正是![]() 对应的期望向量的方向,而
对应的期望向量的方向,而![]() 这个梯度则是把当前的
这个梯度则是把当前的![]() 向其期望靠拢的话,需要的一个向量的差值,这与
向其期望靠拢的话,需要的一个向量的差值,这与![]() 的定义刚好一致
的定义刚好一致
3.3 随机梯度下降
由![]() 的形式我们可以看出,如果想要求它,需要我们把语料库中的V个词全部遍历一遍,当语料库比较大的时候,求一次
的形式我们可以看出,如果想要求它,需要我们把语料库中的V个词全部遍历一遍,当语料库比较大的时候,求一次![]() 的时间开销就十分巨大,因此我们一般不直接使用梯度下降,而是用随机梯度下降的方法来代替。
的时间开销就十分巨大,因此我们一般不直接使用梯度下降,而是用随机梯度下降的方法来代替。
这里不展开讲梯度下降和随机梯度下降的内容,不懂或者感兴趣请自行查阅相关资料,这里仅简单说明使用随机梯度下降时有哪些变化。
求梯度时的变化主要有两个:
(2)变成随机梯度下降之后,我们不能每一轮都检查![]() 是否接近
是否接近![]() (接近
(接近![]() 说明收敛),所以我们固定一个比较大的训练轮数t,训练完t轮之后自动结束
说明收敛),所以我们固定一个比较大的训练轮数t,训练完t轮之后自动结束




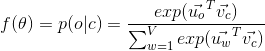
![\frac{\partial f}{\partial{\vec{v_c}}}=\frac{\partial}{\partial \vec{v_c}}log[exp(\vec{u_o}^T\vec{v_c})]- \frac{\partial}{\partial \vec{v_c}}log[\sum_{w=1}^{V}exp(\vec{u_w}^T\vec{v_c})] =f1 - f2](http://img.e-com-net.com/image/info8/045034d015574edca87b00d1f6cf9836.gif)


