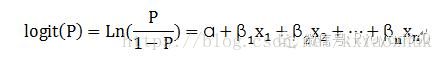逻辑回归模型在R中实践

    在日常学习或工作中经常会使用线性回归模型对某一事物进行预测，例如预测房价、身高、GDP、学生成绩等，发现这些被预测的变量都属于连续型变量。然而有些情况下，被预测变量可能是二元变量，即成功或失败、流失或不流失、涨或跌等，对于这类问题，线性回归将束手无策。这个时候就需要另一种回归方法进行预测，即Logistic回归。

一、Logistic模型简介

Logistic回归模型公式如下：

      

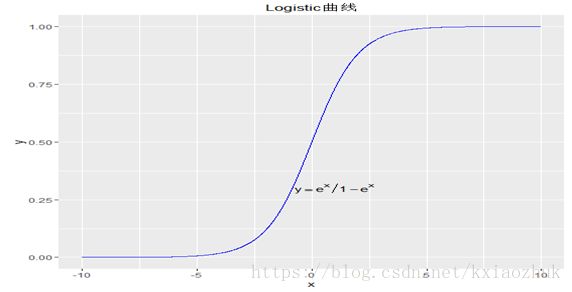
xn的情况下，标签变量y=1时的概率。显然，该模型是一个非线性模型，具有S型分布，可见下图：

#绘制Logistic曲线
x <- seq(from = -10, to = 10, by = 0.01)
y = exp(x)/(1+exp(x))
library(ggplot2)
p <- ggplot(data = , mapping = aes(x = x,y = y))
p + geom_line(colour = 'blue')+ annotate('text', x = 1, y = 0.3, label ='y==e^x / 1-e^x', parse = TRUE)+ ggtitle('Logistic曲线')

由于是非线性模型，从而就少了像线性模型那样的约束，如自变量与因变量具有线性关系、随机误差满足方差齐性等。

以上的模型公式其实是可以变换成线性形式的，只需要一个简单的logit变换即可，即：

二、模型用途

Logistic模型主要有三大用途：

1）寻找危险因素，找到某些影响因变量的"坏因素"，一般可以通过优势比发现危险因素；

2）用于预测，可以预测某种情况发生的概率或可能性大小；

3）用于判别，判断某个新样本所属的类别。

三、模型应用

下文使用Logistic模型对电信行业的客户流失数据进行建模，数据来源为R中C50包自带数据集churnTrain和churnTest。

#使用C50包中自带的电信行业客户流失数据
library(C50)
data(churn)
train <- churnTrain
test <- churnTest
str(train)

数据集中包含了20个变量，其中变量洲(state)、国际长途计划(international_plan)、信箱语音计划(voice_mail_plan)和是否流失(churn)为因子变量，其余变量均为数值变量，而且这里的区域编码变量(area_code)没有任何实际意义，故考虑排除该变量。

#剔除无意义的区域编码变量
train <- churnTrain[,-3]
test <- churnTest[,-3]
#由于模型中，更关心的是流失这个结果(churn=yes)，所以对该因子进行排序
train$churn <- factor(train$churn,levels = c('no','yes'), order = TRUE)
test$churn <- factor(test$churn, ,levels = c('no','yes'), order = TRUE)
#构建Logistic模型
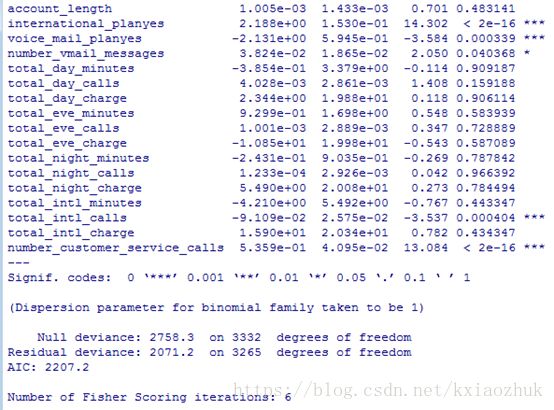
model <- glm(formula = churn ~ ., data =train, family = 'binomial')
summary(model)

发现有很多变量并不显著，故考虑剔除这些不显著的变量，这里使用逐步回归法进行变量的选择(需要注意的是，Logistic为非线性模型，回归系数是通过极大似然估计方法计算所得)。

#step函数实现逐步回归法
model2 <- step(object = model, trace = 0)
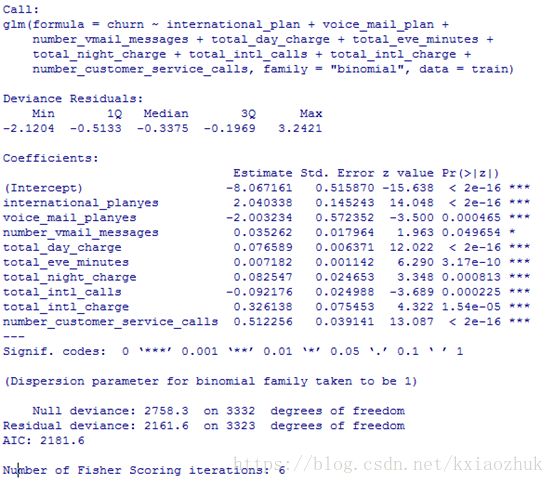
summary(model2)

从结果中发现，所有变量的P值均小于0.05，通过显著性检验，保留了相对重要的变量。模型各变量通过显著性检验的同时还需确保整个模型是显著的，只有这样才能保证模型是正确的、有意义的，下面对模型进行卡方检验。、

#模型的显著性检验
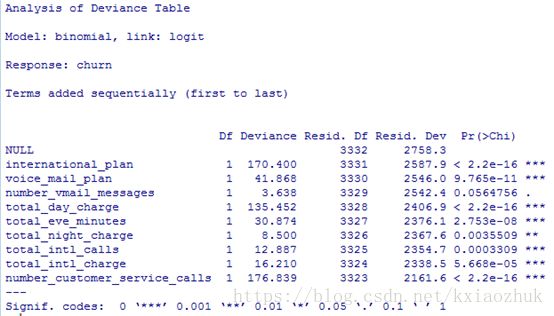
anova(object = model2, test = 'Chisq')

从上图中可知，随着变量从第一个到最后一个逐个加入模型，模型最终通过显著性检验，说明由上述这些变量组成的模型是有意义的，并且是正确的。

虽然模型的偏回归系数和模型均通过显著性检验，但不代表模型能够非常准确的拟合实际值，这就需要对模型进行拟合优度检验，即通过比较模型的预测值与实际值之间的差异情况来进行检验。

Logistic回归模型的拟合优度检验一般使用偏差卡方检验、皮尔逊卡方检验和HL统计量检验三种方法，其中前两种检验适合模型中只有离散的自变量，而后一种适合模型中包含连续的自变量。拟合优度检验的原假设为“模型的预测值与实际值不存在差异”。

#模型的拟合优度检验
library(sjmisc)
HL_test <- hoslem_gof(x = model)
HL_test

从模型的拟合优度检验结果可知，P.value>0.05，该模型接受拟合优度检验的原假设，即可以认为实际值与模型的预测值之间比较接近，不存在显著差异。

以上各项指标均表示模型对电信行业客户流失数据拟合的比较理想，接下来就用该模型对测试集进行预测，预测一个未知的客户是否可能流失，从而起到流失预警的作用。

#模型对样本外数据(测试集)的预测精度
prob <- predict(object = model2, newdata= test, type = 'response')
pred <- ifelse(prob>= 0.5, 'yes','no')
pred <- factor(pred, levels =c('no','yes'), order = TRUE)
f <- table(test$churn, pred)
f

从上图中我们发现：

1).模型对非流失客户(no)的预测还是非常准确的（1408/(1408+35)=97.6%）;

2).模型对流失客户(yes)的预测非常不理想（42/(182+42)=18.8%）

3).模型的整体预测准确率为87.0%((1408+42)/(1408+35+182+42))，还算说得过去。

模型对非流失客户预测精准，而对流失客户预测非常差，我认为的可能原因是模型对非平衡数据非常敏感。即构建模型的训练集中流失客户为483例，而非流失客户为2850例，两者相差非常大。

上文对模型偏回归系数、模型整体和模型拟合优度进行了显著性检验，结果均表明模型比较理想，同时也对模型的预测精度进行验证，也说明了模型的整体预测能力比较理想。接下来我们通过另一种可视化的方法衡量模型的优劣，即ROC曲线，该曲线的横坐标和纵坐标各表示1-反例的覆盖率（正确预测到的正例数/实际正例总数）和正例的覆盖率（正确预测到的负例数/实际负例总数）。

#绘制ROC曲线
library(pROC)
roc_curve <- roc(test$churn,prob)
names(roc_curve)
x <- 1-roc_curve$specificities
y <- roc_curve$sensitivities
library(ggplot2)
p <- ggplot(data = , mapping = aes(x= x, y = y))
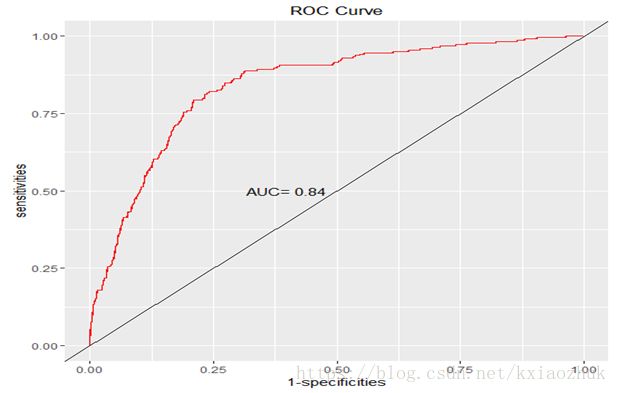
p + geom_line(colour = 'red') +geom_abline(intercept = 0, slope = 1)+ annotate('text', x = 0.4, y = 0.5, label =paste('AUC=',round(roc_curve$auc,2)))+ labs(x = '1-specificities',y = 'sensitivities', title = 'ROC Curve')

通过比较ROC曲线与45°直线可以直观的反映模型的好坏，但并不能从定量的角度反馈模型好是好到什么程度或模型差是差到什么程度。那么就引申出了AUC的概念，这里的AUC为ROC曲线和y=x直线之间的面积。在实际应用中，多个模型的比较可以通过面积大小来选择更佳的模型，选择标准是AUC越大越好。对于一个模型而言，一般AUC大于0.8就能够说明模型是比较合理的了。

统计学中，对于单样本的K-S检验就是利用样本数据来推断其是否服从某种分布，对于两样本的K-S检验主要推测的是两个样本是否具有相同的分布，对于模型的评估，希望正例的累积概率分布与负例的累积概率分布存在显著差异。

所以我们使用K-S统计量刻画模型的优劣，即使正例与负例的累积概率差达到最大。这是一个定量的判断规则，通常要求模型KS值在0.4以上；如下图所示，为传统的评价准则

#计算累计分布函数值
#Kolmogorov-Smirnov检验（柯尔莫哥洛夫-斯摩洛夫），用来检验数据的分布是不是符合一个理论的已知分布
KS_Value <- function(x, y)
{
  gaps_x <- seq(min(x), max(x), length=1000)
  cauculate_x <- numeric()
  for(i in 1:length(gaps_x)){
    cauculate_x[i] <- sum(x<=gaps_x[i])/length(x)
  }
  gaps_x <- sort((gaps_x-min(gaps_x))/(max(gaps_x)-min(gaps_x)))
  gaps_y <- seq(min(y), max(y), length=1000)
  cauculate_y <- numeric()
  for(i in 1:length(gaps_y)){
    cauculate_y[i] <- sum(y<=gaps_y[i])/length(y)
  }
  gaps_y <- sort((gaps_y-min(gaps_y))/(max(gaps_y)-min(gaps_y)))
  return(list(df = data.frame(rbind(data.frame(Gaps = gaps_x,Cauculate = cauculate_x,Type = 'Positive'),data.frame(Gaps = gaps_y,Cauculate = cauculate_y,Type = 'Negtive'))), 
   KS = max(abs(cauculate_y-cauculate_x)), 
   x = gaps_y[which.max(abs(cauculate_y-cauculate_x))],
   y = abs(cauculate_x[which.max(abs(cauculate_y-cauculate_x))]-cauculate_y[which.max(abs(cauculate_y+cauculate_x))])/2))
}
#准备K-S数据
testks <- ifelse(test$churn == "yes", 1, 0)
ks_data <- as.data.frame(cbind(good_bad=testks, prob ))
good_ks <- ks_data[which(ks_data$good_bad==0),'prob']
bad_ks <- ks_data[which(ks_data$good_bad==1),'prob']
#生成K-S值
ks <- KS_Value(bad_ks,good_ks) #KS_Value属于上面自定义的KS值函数
#绘制K-S曲线
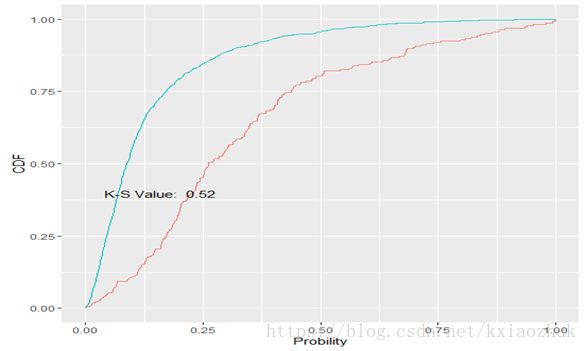
ggplot(data = ks$df, mapping = aes(x = Gaps, y = Cauculate, colour = Type)) + geom_line() + theme(legend.position='none') + annotate(geom = 'text', x = ks$x, y = ks$y, label = paste('K-S Value: ', round(ks$KS,2))) + labs(x = 'Probility', y = 'CDF')  

上图结果显示，K-S统计量的值为0.52，根据传统的评价准则，也说明该模型很好。