shader 利用FBM， noise 模拟海洋波浪

 

梯度噪声

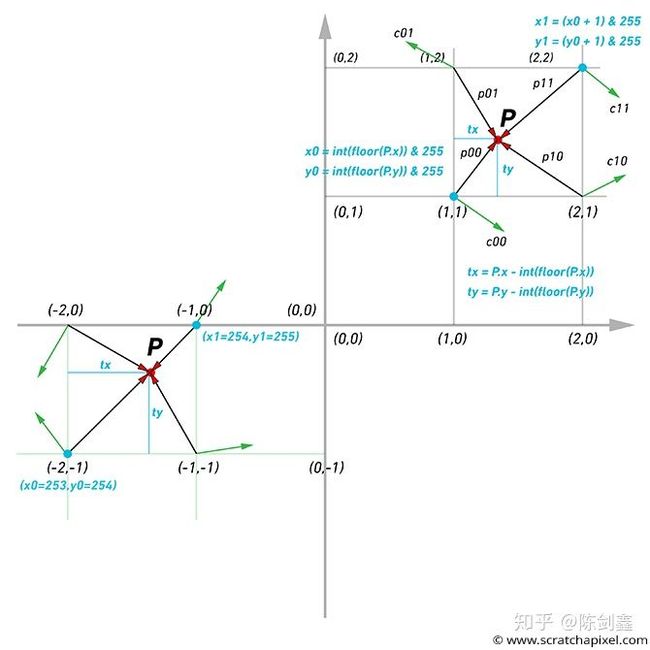
梯度噪声的主要原理是将坐标系划分成一块一块的晶格之后在晶格的每个顶点处生成一个随机的梯度（可以理解成方向向量），然后在计算噪声的时候会综合计算该噪声所在的晶格的顶点上的方向向量（图中绿色箭头）进行聚合计算（可以理解成加权计算合力）。

图片来自 scratchapixel

Perlin噪声就属于这一类，所以这样一来我们就可以封装一个Perlin噪声的函数了：

// reference shadertoy
float perlinNoise(vec2 p) {
    vec2 pi = floor(p);
    vec2 pf = fract(p);

    vec2 w = pf * pf * (3.0 - 2.0 * pf);

    return mix(mix(dot(hash22(pi + vec2(0.0, 0.0)), pf - vec2(0.0, 0.0)), 
                   dot(hash22(pi + vec2(1.0, 0.0)), pf - vec2(1.0, 0.0)), w.x), 
               mix(dot(hash22(pi + vec2(0.0, 1.0)), pf - vec2(0.0, 1.0)), 
                   dot(hash22(pi + vec2(1.0, 1.0)), pf - vec2(1.0, 1.0)), w.x),
               w.y);
}

FBM

这样看起来似乎并不怎么自然，不就是渐变的效果而已嘛，但是如果再加上了fbm（分形布朗运动）之后，那就大不一样了。

const mat2 mtx = mat2( 0.80,  0.60, -0.60,  0.80 );
float fbm6( vec2 p ) {
  float f = 0.0;

  f += 0.500000*perlinNoise( p ); p = mtx*p*2.02;
  f += 0.250000*perlinNoise( p ); p = mtx*p*2.03;
  f += 0.125000*perlinNoise( p ); p = mtx*p*2.01;
  f += 0.062500*perlinNoise( p ); p = mtx*p*2.04;
  f += 0.031250*perlinNoise( p ); p = mtx*p*2.01;
  f += 0.015625*perlinNoise( p );

  return f/0.96875;
}

效果如下：

除此之外，Simplex噪声也是属于这种原理，只不过它的晶格的定义有所不一样。Perlin噪声的晶格是和噪声空间（噪声的维度）保持平行的，比如1D的是单位线段、2D空间是正方形、3D空间是立方体以此类推。

但是Simplex噪声采用的是最小包围晶格，比如1D的是单位线段、2D空间是三角形、3D空间是三角锥，然后以此类推。这样的的话就可以保证Simplex噪声在高维度的时候能有更好的计算性能，因为需要更少的插值计算。

更多的信息可以查看这里 Simplex噪声。

Value噪声

Value噪声就很简单了，它是区别于梯度噪声的，将晶格顶点的随机梯度向量直接简单粗暴的以随机数值来代替。在计算时直接进行加权插值即可，减少了很多点乘操作，因此它的性能也比Perlin噪声要更好一点。

float valueNoise(vec2 p) {
  vec2 w = floor(p);
  vec2 k = fract(p);
  k = k*k*(3.-2.*k); // smooth it

  float n = w.x*10. + w.y*48.;

  float a = hash(n);
  float b = hash(n+10.);
  float c = hash(n+48.);
  float d = hash(n+58.);

  return mix(
    mix(a, b, k.x),
    mix(c, d, k.x),
    k.y);
}

因为插值计算得更简单，所以看起来的初步效果会比较硬，会有明显的晶格（小方块）的痕迹：

但是不要怕，没有什么事情是fbm（分形布朗运动）不能解决的（如果有那就多用几遍）

const mat2 mtx = mat2( 0.80,  0.60, -0.60,  0.80 );
float fbm6( vec2 p ) {
  float f = 0.0;

  f += 0.500000*valueNoise( p ); p = mtx*p*2.02;
  f += 0.250000*valueNoise( p ); p = mtx*p*2.03;
  f += 0.125000*valueNoise( p ); p = mtx*p*2.01;
  f += 0.062500*valueNoise( p ); p = mtx*p*2.04;
  f += 0.031250*valueNoise( p ); p = mtx*p*2.01;
  f += 0.015625*valueNoise( p );

  return f/0.96875;
}

粗糙的初始噪声经过fbm之后都会变的非常自然。

首先给出fbm的计算公式 fbm = noise(uv) + 0.5 * noise(2* uv) + 0.25 * noise(4 * uv)  + 0.125 * noise(8 * uv)

这里的noise采用细胞噪声的模型：

具体细胞模型可以参考：网格噪声

 可以在shadertoy进行试验观察效果 

具体源码：

#define DEEP 20
float random(vec2 uv) {
	return fract(sin(dot(uv.xy,vec2(13.0909,783.342))) * 423234.323);
}
vec2 random2(vec2 uv){
    float res = fract(sin(dot(uv.xy,vec2(132.090,989.232))) * 232324.123);
	return vec2(res);
}
vec3 cellNoise(vec2 uv) {
	uv *= 3.0;
    vec2 i_st = floor(uv);
    vec2 f_st = fract(uv);
    
    /*vec2 point = random2(i);
    vec2 dist = point - f;
    float di = length(dist);
    */
    vec3 color = vec3(0.);
    float m_dist = 1.;
    for(int i = -1; i <=1; i++) {
        for(int j = -1; j <= 1; j++) {
            vec2 neighbor = vec2(float(j),float(i));
        	vec2 point = random2(i_st + neighbor);
            point = 0.5 + 0.5 * sin(iTime + 6.283 * point);
            // 像素点到随机点的距离
            vec2 diff = neighbor + point - f_st;
            float dist = length(diff);
            m_dist = min(m_dist,dist);
        }
    }
    color += m_dist;
    return color;
}
vec3 fbm_noise(vec2 uv) {
    vec3 res = vec3(0.);
    float a = 0.0;
    float b = 0.0;
    for(int i = 0; i < DEEP; i++) {
        a += (float(i) + 1.);
        b = 1. / a;
    	res += b * cellNoise(a * uv);
    }
	return res;
}
void mainImage( out vec4 fragColor, in vec2 fragCoord )
{
    // Normalized pixel coordinates (from 0 to 1)
    vec2 uv = fragCoord/iResolution.xy;
    // 网格化像素坐标
    
    vec3 color = fbm_noise(uv);
    
    fragColor = vec4(color,1.0);
}

具体效果如下：