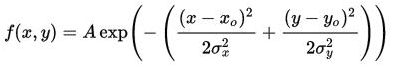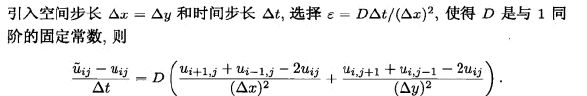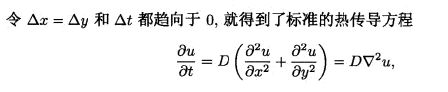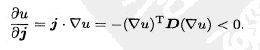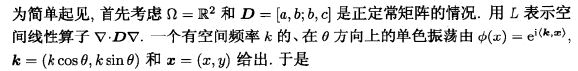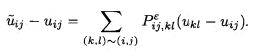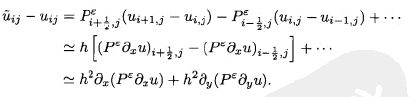热传导与图像处理:非线性各项异性扩散
首先,用通俗的语言说明两个基本概念,非线性和各向异性
非线性,可以从线性说起,不严谨的说,如果两个变量之间的关系是一次函数,那么就说他们是线性关系,比如一维的一条直线:
y=kx+b,k和b都是实数,表示为:
![]()
两者关系不是线性的,那就是非线性的,典型的,多次函数,幂指数,逻辑函数等。
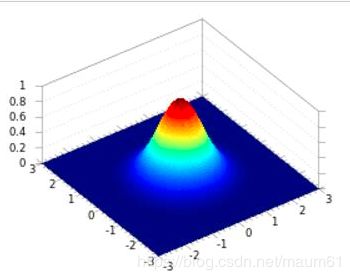
各向异性,先从各项同性说起。这个可以举一个简单的例子,二维高斯函数,只要该点离高斯中心点的距离相同,那么得到的函数值就相同:
例如,上图中颜色相同的等高线,不管该点处于哪个方向,只要离中心点的距离相同,那么值就是相同的。这个简单的例子可以帮助我们理解各项同性,那么很自然的想到,如果将上述高斯函数做一点小变化,把x变为x/2,那么等高线就不再是圆了,各当方向不同的时候,尽管距离相同,那值也是不同的,因此是各向异性的。
这两个概念有助于我们理解各向异性扩散的核心思想。
各向异性扩散滤波,是一种针对噪声的保边滤波器,保边意思就是在磨平噪声的同时,保留边沿。因为大多数的噪声是孤立的点,就像是二维高斯函数的图像一样,是各向同性的,影响图像质量。而有意义的目标边沿,其边沿点一般不是孤立的,表现为线、拐角等,这些是有意义的信息,在滤波的过程中应该保留。那很自然的一种想法就是使用各向异性类型的滤波器。
拉普拉斯滤波器是提取图像边沿信息的有效工具之一,经过拉氏算子卷积后的特征图,体现了原图像中的极值点信息,其实也是一种高频信息,具体表现为,如果这个像素是极大值,则特征图像素值为负,如果是极小值点,特征图像素值为正。仅有x和y方向的5像素拉氏滤波器模板表示为:
![]()
使用迭代法,计算每一步滤掉的那一部分图像:
![]()
那么,等式右侧就是图像对x,y方向的二阶偏导:
在图像中也就是迭代一次得到的图像与迭代前图像的差,它和原图像是同型的。
这个标准的热传导方程是线性扩散方程,也就是说,这里的D是与1同阶的固定常数,简单理解为一个固定实数。
这个迭代过程和热扩散过程就是等价的。此时,还不是各项异性,因为对x和y的偏导部分系数都是一样的,都是D,如果将D改写为一个关于位置(x,y)的对角阵,或者更一般的正定矩阵:
![]()
那么扩散过程就变为了:
注意这里的D是作用在了u的梯度图上后,再求散度的,证明它是和x,y相关的,同时,这里引入了![]() ,也就是二阶偏导,就是对y求偏导后再对x求偏导。当a、b、c不完全相等时,该扩散就是各项异性的了,同时D是一阶函数,这就是线性各项异性扩散。这个扩散的驱动力就是像素强度分布的不均匀性
,也就是二阶偏导,就是对y求偏导后再对x求偏导。当a、b、c不完全相等时,该扩散就是各项异性的了,同时D是一阶函数,这就是线性各项异性扩散。这个扩散的驱动力就是像素强度分布的不均匀性![]() 。
。
而通量公式:
![]()
只要保证D是正定的,那么通量肯定是梯度衰减的:
因此,扩散过程会磨平大的梯度,尤其是各个方向的梯度值是一致的随机噪声引起的局部振荡。
而振荡的剧烈程度和扩散程度之间的关系可以由一个简单的例子说明:
因为D是正定的,![]() >0,那么
>0,那么![]() >0,这说明线性空间的这个扩散算子L作用在这个单色振荡上,就相当于是乘了一个系数(这里
>0,这说明线性空间的这个扩散算子L作用在这个单色振荡上,就相当于是乘了一个系数(这里![]() 和
和![]() 可以看做是矩阵L的特征值和特征向量。因此仅仅是对
可以看做是矩阵L的特征值和特征向量。因此仅仅是对![]() 的缩放),而缩放程度
的缩放),而缩放程度![]() =
=![]() =O(k^2),也就是与k平方线性相关的值,所以k越大,扩散的越厉害,是呈平方关系增长的。
=O(k^2),也就是与k平方线性相关的值,所以k越大,扩散的越厉害,是呈平方关系增长的。
非线性各项异性扩散,就是将线性的D变为了非线性的P:
这个形如高斯函数的非线性扩散系数,是为了在宏观上保持图像的边。它可以平衡由梯度大小而导致的扩散不均匀,因为如果是线性的,梯度大,那么它对整个扩散的贡献就会大,导致扩散速度加快,而梯度小,其作用就会微不足道。其实这是符合热扩散原理的,但是为了在宏观上保持图像的边,需要将制衡不同梯度的贡献率,因此这个自适应的函数达到的目的是,降低大梯度的贡献率,保持小梯度的贡献率。扩散方程就变为了:
则有:
这里将![]() ,是契合了数字图像求偏导的想法,求得的偏导不是该像素点的,而近似是
,是契合了数字图像求偏导的想法,求得的偏导不是该像素点的,而近似是![]() 这个像素点的偏导,更像是拉格朗日中值定理描述的那样,将像素间跃变认为是线性的,因此这么记会更确切。
这个像素点的偏导,更像是拉格朗日中值定理描述的那样,将像素间跃变认为是线性的,因此这么记会更确切。
这时做如下变换,将:
![]() ,对
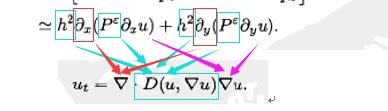
,对![]() 取极限,便得到了非线性扩散方程:
取极限,便得到了非线性扩散方程:
![]()
这里的变化可以通过下面的图加以辅助理解:
那么扩散后也即是滤波后的图像可以表达为:
![]()
这也是基于各项异性扩散的图像融合方法里所用到的理论基础:
D.P. Bavirisetti, R. Dhuli, Fusion of infrared and visible sensor images based on anisotropic diffusion and karhunen-loeve transform, IEEE Sensors J. 16 (1) (2016) 203–209.