算法竞赛入门经典第11章 最小生成树 Kruskal（克鲁斯卡尔）算法 和 Prim（普利姆）算法 详解及C++实现

考虑几个城市之间需要道路连通，每两个城市之间建设道路的费用不同，我们建设道路时，不一定需要在每两个城市A和B之间直接铺设道路，A城市能通过其它城市到达B城市即可。如何建设才能使费用最低呢？

这就是最小生成树问题。可以假设开始时每两个城市之间都有道路连通，我们选出一些道路，去掉其它道路，使得总费用最低。可以想象生成的道路不存在环，否则可以通过去掉环的一个边，使得环上的城市依旧连通。在了解算法之前，需要先知道几个基本概念：

1. 连通图：在无向图中，若任意两个顶点$u$与$v$都有路径相通，则称该无向图为连通图。

2. 连通子图：通过去掉一些边，使连通图仍然保持连通，得到的图称为连通子图，一个连通图可能有多个连通子图。

3. 生成树：一个连通图的生成树是指一个连通子图，它含有图中全部n个顶点，但只有足以构成一棵树的n-1条边。一颗有n个顶点的生成树有且仅有n-1条边，如果生成树中再添加一条边，则必定成环。

4. 最小生成树：在一个图的所有连通子图中，所有边的权值相加最小的生成树，称为最小生成树。

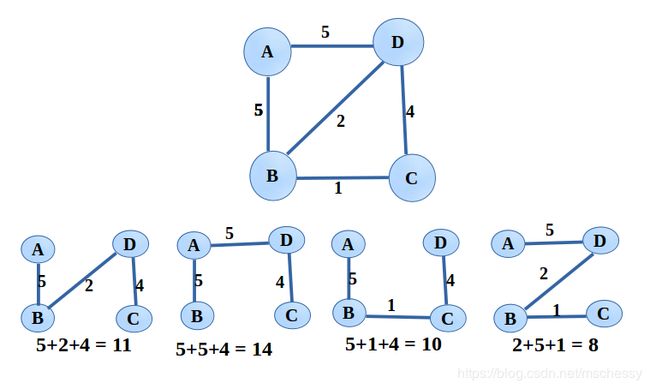
上图为一个连通图的四个不同权值的连通子图(生成树)，第四个连通图的权值最低，是该图的最小生成树。

构造最小生成树的过程可以用贪心算法，和我们去掉道路的过程相反，假设最开始没有边，不断找到权值最小的合法道路（加上道路以后没有环）并添加到图里。常用的算法有两个：Kruskal（克鲁斯卡尔）算法 和 Prim（普利姆）算法。

Kruskal算法

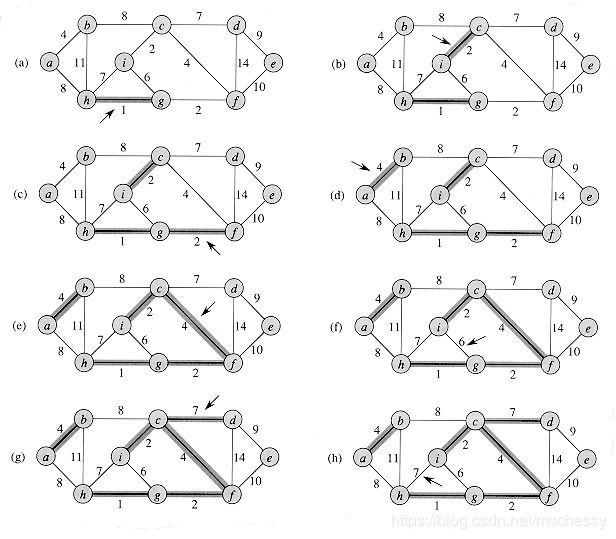
Kruskal算法又称为”加边法“，首先按权值排序边，然后选择未选择过的权值最小的一条边，并检查该边是否合法（加上以后不成环即合法，成环即不合法），如果合法就加上该边，然后在未选择过的边中继续遍历，一直到所有顶点都连通。

我们可以将连通的点看作一个集合，最开始的时候，每个点自成一个集合，并没有两个点在一个集合中。当我们找到一条边并将这条边加入图中，相当于边的两条端点合并为同一集合。如果找到的权值最小的边的两个端点已经在同一集合中，需要跳过它继续检查下一条边。

用三个数组u, v, w分别保存每条边的起点，终点，权值。数组p保存每个节点的父亲节点。注意这里：

int find (int x)
{
    return p[x] == x ? x : p[x] = find(p[x]);
}

在寻找父亲节点的过程中，可以将这个父亲节点下的所有节点都连接到根节点上，也就是并查集的思想，这样在下次查找的时候不用沿着长长的链一直走，会提高效率。

Kruskal方法完整代码：

#include
#include
#include
using namespace std;

int n = 10;
vector<int> u(n), v(n), w(n), r(n), p(n); //第i条边的起点，终点，权值，按权值排序后的边序号，父亲节点
vector<pair<int, int>> res;
bool cmp (int a, int b)
{
    return w[a] < w[b];
}

int find (int x)
{
    return p[x] == x ? x : p[x] = find(p[x]);
}

int kruskal ()
{
    int cost = 0;
    for(int i = 0; i < n; i++)
    {
        int x = find(u[r[i]]);
        int y = find(v[r[i]]);
        if(x != y)
        {
            cost += w[r[i]];
            p[x] = y;
            res.push_back(make_pair(u[r[i]], v[r[i]]));
        }
    }
    return cost;
}

int main ()
{
    u = {1, 1, 1, 2, 2, 3, 3, 4, 4, 5};
    v = {2, 6, 5, 3, 6, 4, 6, 5, 6, 6};
    w = {6, 7, 10, 3, 5, 8, 9, 4, 2, 1};
    for(int i = 0; i < n; i++){
        //cin >> u[i] >> v[i] >> w[i];
        r[i] = i;
        p[i] = i;
    }
    sort (r.begin(), r.end(), cmp);
    int sum = kruskal ();
    cout<<"Total cost: "<<sum<<endl;
    for(int i = 0; i < res.size(); i++)
        cout<<res[i].first<<", "<<res[i].second<<" || ";
    return 0;
}

输出结果：

Prim算法
Prim算法又称加点法，定义一个已访问过的集合S(代码中使用bool数组vis实现)，算法从某一个顶点s开始，先将点s加入集合S，检查与S连接且另一端点不在S内的边，找到权值最小的边加入到生成树中，该边另一端点加入集合S，重复步骤一直到所有顶点都访问过。

1. 确定一个起点，检查以该点为端点的所有边；
2. 将该点标记为已访问，在已经寻找的边中发现最小边，这个边必须有一个点还没有访问过，将还没有访问的点加入我们的集合，记录添加的边；
3. 寻找当前集合可以访问的所有边，找到与当前集合内任意点距离最短的边，重复2的过程，直到没有新的点可以加入， 此时生成的树为最小生成树。
   

完整代码（使用邻接矩阵G）：

#include
#include
#include
#include
using namespace std;

struct line //定义一个边类，u和v为该边的两个端点，distance为该边到集合的距离
{
    int u = 0;
    int v = 0;
    int distance = INT_MAX;
};

int e = 10, n = 6; //边数e和顶点数n
vector<line> d(n+1);
vector<bool> vis(n+1, false); //标记已访问的点
vector<vector<int>> G(n+1, vector<int> (n+1, INT_MAX)); //邻接矩阵
vector<pair<int, int>> res; //记录结果

int prim()
{
    d[1].distance = 0;
    int cost = 0;

    for(int i = 1; i <= n; i++)
    {
        int u = -1;
        int MIN = INT_MAX;
        for(int j = 1; j <= n; j++)
            if(!vis[j] && d[j].distance < MIN) //寻找另一端点没有访问过且与已访问过的点的集合距离最短的边
            {
                MIN = d[j].distance; 
                u = j;
            }
        if(u < 0) return -1; //图不连通，无解，返回-1
        vis[u] = true;
        cost += d[u].distance;
        res.push_back({d[u].u, d[u].v}); //将该边加入图中，点u加入已访问的点的集合
        for(int v = 1; v <= n; v++)
            if(G[u][v] != INT_MAX && !vis[v] && G[u][v] < d[v].distance)
            {
                d[v].distance = G[u][v];
                d[v].u = u;
                d[v].v = v;
            }
    }
            for(int i = 1; i < res.size(); i++)
            cout << res[i].first << ", " << res[i].second<<" || ";

    return cost;
}

int main ()
{
    vector<int> u(e), v(e), w(e);
    u = {1, 1, 2, 2, 3, 3, 5, 4};
    v = {2, 6, 3, 5, 4, 5, 6, 5};
    w = {5, 2, 8, 4, 3, 7, 6, 9};
    for(int i = 0; i < e; i++)
        G[u[i]][v[i]] = G[v[i]][u[i]] = w[i];
    int sum = prim ();
    cout<<endl<<"Total cost: "<<sum<<endl;
    return 0;
}

结果：