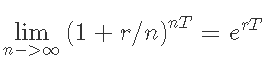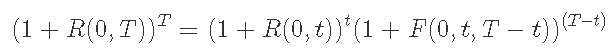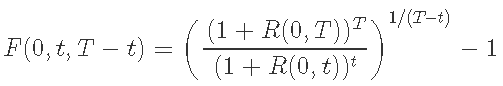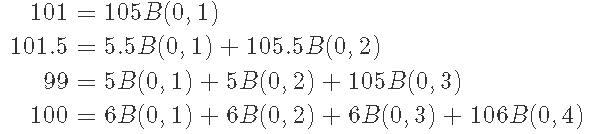用R语言用Nelson Siegel和线性插值模型对债券价格和收益率建模

原文链接：http://tecdat.cn/?p=11758

---

 

债券基础 

• 键  是一个合同，作者与初始付款义务以预定的时间（s）（成熟）的钱付预定量。这类似于借入利息和付款结构的钱。
• 零息债券  是一种特殊类型的键，其在到期时支付出仅一次没有中间付款。
• 债券的面额/票面金额/本金是发行人在到期时所支付的金额。标准价值通常为$ 1000。
• 债券可以参考价格或收益。例如，将支付$ 100的零息债券的价格可以是$ 90。但收益率将是（100-90）/ 90 = 11％（100-90）/ 90 = 11％，而不是10％10％。
• 债券价格的一个常见约定是，它们最终收于100。这就是为什么当利率上升时，债券价格下降，反之亦然。另一种惯例是美分兑美元（例如，90美分兑美元）。
• 债券收益率被称为年利率。例如，十年期政府债券的收益率为2％，这意味着它的年收益将为2％，而不是10年后。
• 债券可以在二级市场上交易（一级市场是债券发行过程）。如果利率增加，债券的价值就会增加，如果利率降低，债券的价值就会减少，这仅仅是因为该债券是在利率改变之前以便宜/昂贵的价格发行的。也可以做空债券。
• 即使不期望债券产生负利率，也不是完全看不见的。在危机时期，政府债券甚至公司债券可以负收益进行交易。

定价债券

债券价格是通过使用票面利率和现金流量确定债券的现值来确定的。

 

其中CFt是时间tt的现金流量，B（0，t）是美元的折扣率或时间00的价格。

 

其中R（0，t）是在时间为tt时在时间00的年度即期汇率。我们可以重新安排

 

B（0，t）也可以称为零息债券的价格。大多数债券不是零息债券，但是有可能使用零息债券构造几乎所有支付结构。

我们可以暗示与市场债券不同期限的零息票利率。然后，我们可以使用这些利率建立期限结构模型来对任何债券定价。严格违反期限结构可能是买卖机会，也可能是套利机会。

calculate_bond_price<-function(face_value=1000,coupon_rate=0.05,maturity=1,yearly_coupons=0){
    #This function calculates the price of the bond B(0,t) given
    #its face value, maturity, annual coupon rate and equidistant payment
    #if yearly_coupons == 0, it only pays out at the maturity
    #if yearly_coupons == 1, it pays out annually
    #if yearly_coupons == 2, it pays out semiannually
    if(yearly_coupons==0){
        face_value/((1+coupon_rate)^maturity)
    }else{
        face_value/((1+coupon_rate/yearly_coupons)^(yearly_coupons*maturity))
    }

}
calculate_bond_price()

## [1] 952.381

如果我们有适当的证券，我们也可以从付息债券中构造零息债券。从讲义中假设我们有两个纽带。

• 1年期纯贴现债券在$ 95出售。
• 两年期8％的债券售价99美元。

 

 

2年期纯折价债券的价格为99-0.08（95）= 91.499-0.08（95）= 91.4（通过买入两年期债券多头和买入一年期债券空头0.08个单位（以抵消第一个债券的收益）年优惠券）。

复利类型

简单复合

这是仅应用一次利率的方法。假设利率为0.05，期限为2年。100美元的价格在到期时将是多少。

 

定期复利

如果将利息永久添加到本金投资中，那么我们的复利就是利率。假设相同的示例，但每半年复算一次。

 

产生的年名义利率为  。

连续复利

现在，假设复利的频率很高，以至于在两次加息之间的时间间隔是无限的（接近零）。然后在极限情况下

 

看起来很熟悉？

因此，以我们的示例为例，连续复利的年利率是 

给定一组零息票债券价格，我们可以计算连续收益率 

#Example bond price is 0.987 and maturity is half a year.
calculate_yield(0.987,0.5)

## [1] 0.02617048

远期汇率

假设有两个到期日不同的债券

可以重新排列成

 

imply_forward_rate<-function(R0t1=0.04,R0t2=0.045,t1=1,t2=2){

    ((1+R0t2)^t2/(1+R0t1)^t1)^(1/(t2-t1)) -1

}
imply_forward_rate()

## [1] 0.05002404

到期日的相关性

利率不仅随着到期日变化，而且随着时间变化。我们还将调用某些数据和计算。

让我们加载库并检查美联储收益率曲线数据。

##             R_3M  R_6M  R_1Y  R_2Y  R_3Y  R_5Y  R_7Y R_10Y
## 1981-12-31 12.92 13.90 14.32 14.57 14.64 14.65 14.67 14.59
## 1982-01-31 14.28 14.81 14.73 14.82 14.73 14.54 14.46 14.43
## 1982-02-28 13.31 13.83 13.95 14.19 14.13 13.98 13.93 13.86
## 1982-03-31 13.34 13.87 13.98 14.20 14.18 14.00 13.94 13.87
## 1982-04-30 12.71 13.13 13.34 13.78 13.77 13.75 13.74 13.62
## 1982-05-31 13.08 13.76 14.07 14.47 14.48 14.43 14.47 14.30

相关矩阵显示出收益率没有完全相关，因此时间形状会发生变化。

	R_3M	R_6M	R_1Y	R_2Y	R_3Y	R_5Y	R_7Y	R_10Y
R_3M	1.0000000	0.9983390	0.9940045	0.9837559	0.9744780	0.9546189	0.9399504	0.9230412
R_6M	0.9983390	1.0000000	0.9981715	0.9899820	0.9817197	0.9632268	0.9491761	0.9332366
R_1Y	0.9940045	0.9981715	1.0000000	0.9959937	0.9900195	0.9746174	0.9621895	0.9478956
R_2Y	0.9837559	0.9899820	0.9959937	1.0000000	0.9984844	0.9896811	0.9808896	0.9694621
R_3Y	0.9744780	0.9817197	0.9900195	0.9984844	1.0000000	0.9958583	0.9896185	0.9804575
R_5Y	0.9546189	0.9632268	0.9746174	0.9896811	0.9958583	1.0000000	0.9983629	0.9936744
R_7Y	0.9399504	0.9491761	0.9621895	0.9808896	0.9896185	0.9983629	1.0000000	0.9981232
R_10Y	0.9230412	0.9332366	0.9478956	0.9694621	0.9804575	0.9936744	0.9981232	1.0000000

债券价格和收益率

在这一部分中，我们将看到提取和构建债券价格和收益率的方法。

直接法

假设您得到以下债券利率。请记住，名义汇率是100。

	优惠券	到期	价钱
债券1	5.0	1个	101.0
债券2	5.5	2	101.5
债券3	5.0	3	99.0
债券4	6.0	4	100.0

零息债券价格（B（0，t）B（0，t）

然后我们得到 

get_zero_coupon()

## $B0t
## [1] 0.9619048 0.9119386 0.8536265 0.7890111
## 
## $R0t
## [1] 0.03960396 0.04717001 0.05417012 0.06103379

线性插值

R03<-0.055
R04<-0.06

R03p75<-((4-3.75)*0.055+(3.75-3)*0.06)/(4-3)
R03p75

## [1] 0.05875

##Or use the R function
yield_interpolate<-approxfun(x=c(3,4),y=c(0.055,0.06))
yield_interpolate(3.75)

## [1] 0.05875

三次插值

假设我们的费率如下： 

#Interpolate for a bond of 2.5 years
t_val<-2.5
sum(abcd_vec*((2.5)^(3:0)))

## [1] 0.0534375

## [1] 0.0534375

间接方法（Nelson Siegel）

代替引导技术，我们将使用模型。尼尔森·西格尔（Nelson Siegel）模型是模拟利率收益率曲线的一种流行方法。

 

其中θ是到期日，β0是级别参数（长期收益率），β1是斜率参数（长期/短期扩展），β2是曲率参数，τ是比例参数。

ns_data <-
data.frame(maturity=1:30) %>%
mutate(ns_yield=nelson_siegel_calculate(theta=maturity,tau=3.3,beta0=0.07,beta1=-0.02,beta2=0.01))

head(ns_data)

##   maturity   ns_yield
## 1        1 0.05398726
## 2        2 0.05704572
## 3        3 0.05940289
## 4        4 0.06122926
## 5        5 0.06265277
## 6        6 0.06376956

ggplot(data=ns_data, aes(x=maturity,y=ns_yield)) + geom_point() + geom_line()

可以使用参数来更好地估计收益曲线。

Nelson Siegel参数的估计

YieldCurve 上述R包  具有Nelson Siegel曲线估计功能。

##              beta_0     beta_1   beta_2    lambda
## 1981-12-31 14.70711 -5.3917409 3.269125 0.5123605
## 1982-01-31 14.35240 -0.7602066 2.834508 0.1887807
## 1982-02-28 13.74481 -0.9247232 2.681840 0.1236869

注意：我们将lambda称为tau（ττ）（形状参数）。

Beta灵敏度

考虑提供Fi未来现金流的债券价格  。因此，带有beta参数的价格变化如下。

 

nelson_siegel_sensitivities(coupon_rate=0.05,maturity=2)

##      Beta0      Beta1      Beta2 
## -192.51332 -141.08199  -41.27936

nelson_siegel_sensitivities(coupon_rate=0.05,maturity=7)

##     Beta0     Beta1     Beta2 
## -545.4198 -224.7767 -156.7335

nelson_siegel_sensitivities(coupon_rate=0.05,maturity=15)

##     Beta0     Beta1     Beta2 
## -812.6079 -207.1989 -173.0285

---

1. 这些R讲义也将遵循固定收益证券：Martellini，Priaulet和Priaulet撰写的“估值风险管理和投资组合策略”。

2. 债券可以在收益率之上额外溢价或折价购买或出售。纯折扣意味着没有额外的折扣或溢价。