【图像处理】LBP特征
参考
人脸识别经典算法二:LBP方法
人脸识别算法-LBP算法及python实现
LBP特征提取
LBP(Local Binary Patterns,局部二值模式),常用于人脸识别。
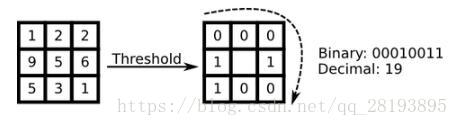
最初的LBP是定义在像素3x3邻域内的,以邻域中心像素为阈值,将相邻的8个像素的灰度值与其进行比较,若周围像素值大于中心像素值,则该像素点的位置被标记为1,否则为0。这样,3x3邻域内的8个点经比较可产生8位二进制数(通常转换为十进制数即LBP码,共256种),即得到该邻域中心像素点的LBP值,并用这个值来反映该区域的纹理信息。如下图所示:
公式表述如下:
其中, (xc,xc) ( x c , x c ) 表示3x3邻域的中心元素,它的像素值为 ic i c , ip i p 代表邻域内像素值。 s(x) s ( x ) 定义如下:
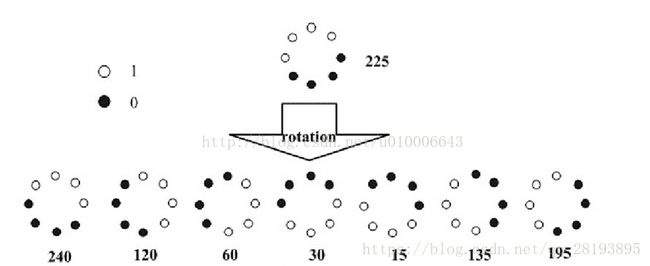
旋转不变性:
如上图所示,这个点的LBP值是11100001 = 225,这时候我们开始旋转,可以看到每一个情况都旋转到了,我们取这些情况中的最小值,也就是15,作为这个点的LBP值,这样不管图片怎么旋转,这个点的LBP值都会是15,也就是旋转不变性。
算子改进
基本的 LBP算子的最大缺陷在于它只覆盖了一个固定半径范围内的小区域,这显然不能满足不同尺寸和频率纹理的需要。
为了适应不同尺度的纹理特征,并达到灰度和旋转不变性的要求,Ojala等对 LBP 算子进行了改进,将 3×3邻域扩展到任意邻域,并用圆形邻域代替了正方形邻域,改进后的 LBP 算子允许在半径为 R 的圆形邻域内有任意多个像素点。从而得到了诸如半径为R的圆形区域内含有P个采样点的LBP算子。比如下图定了一个5x5的邻域:
LBP等价模式
一个LBP算子可以产生不同的二进制模式,对于半径为R的圆形区域内含有P个采样点的LBP算子将会产生 2P 2 P 种模式。很显然,随着邻域集内采样点数的增加,二进制模式的种类是急剧增加的。如此多的二值模式无论对于纹理的提取还是对于纹理的识别、分类及信息的存取都是不利的。因此,需要对原始的LBP模式进行降维,使得数据量减少的情况下能最好的代表图像的信息。
Ojala提出了采用一种“等价模式”(Uniform Pattern)来对LBP算子的模式种类进行降维。因此,Ojala将“等价模式”定义为:当某个LBP所对应的循环二进制数从0到1或从1到0最多有两次跳变时,该LBP所对应的二进制就称为一个等价模式类。如00000000(0次跳变),00000111(只含一次从0到1的跳变),10001111(先由1跳到0,再由0跳到1,共两次跳变)都是等价模式类。除等价模式类以外的模式都归为另一类,称为混合模式类,例如10010111(共四次跳变)。比如下图给出了几种等价模式的示意图:
通过这样的改进,二进制模式的种类大大减少,而不会丢失任何信息。模式数量由原来的 2P 2 P 种减少为 P(P−1)+2 P ( P − 1 ) + 2 种,其中P表示邻域集内的采样点数。对于3×3邻域内8个采样点来说,二进制模式由原始的256种减少为58种,这使得特征向量的维数更少,并且可以减少高频噪声带来的影响。
LBP特征匹配
将一副人脸图像分为7x7的子区域,并在子区域内根据LBP值统计其直方图,以直方图作为其判别特征。这样做的好处是在一定范围内避免图像没完全对准的情况,同时也对LBP特征做了降维处理。
分区的意义还在于我们可以根据不同的子区域给予不同的权重,比如说我们认为鼻子的权重大于边缘子区域对于整个图片的权重。权重的意思也就是这个部分对于匹配时整个图片的意义。我们根据LBP值统计直方图,上面提到的LBP值有 28=256 2 8 = 256 种,其实也就是一个灰度图的直方图统计过程。只要我们把LBP值看做一个新的像素值。
相似性判别方法
(1)直方图交叉核方法
(2)卡方统计方法