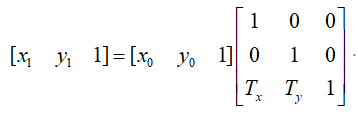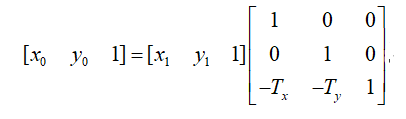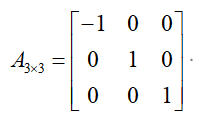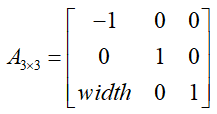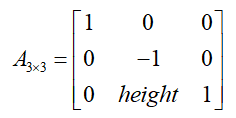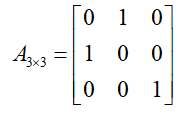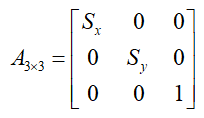数字图像处理（5）—— 图像的几何变换

先祝大家新年快乐！！！！这段时间确实有点忙，然后每个图像都用MATLAB重新调一遍工作量确实有点大，后面可能会少一些。其实说白了，图像处理本质上在 MATLAB 里面就是矩阵运算。线性代数没学过或者比较不熟悉的的可以自己了解一下，感觉不是很复杂，相信看完了《线性代数》你会对图像处理有新的认识。深一些的就是《矩阵论》了。强调一下：思想真的很重要！！！然后就是基础知识，某些大佬也称为“元知识”，也很重要！！！

目录

1、前言

2、几何变换的常用解决思路——伪算法

3、几何变换方法

3.1、图像的平移变换

3.2 图像的镜像

3.3 图像的转置

3.4 图像的缩放

---

1、前言

        我们知道，同一幅图像可能会因为角度、对称性、透视关系、大小等等因素使图像各个位置的像素灰度几乎完全不同，但是我们肉眼直观地看上去实际上是同一幅图像，只是几何形状发生了变化。那么如何得到一幅图像的几何变换后的输出图像，就是这篇要讨论的问题。

        几何变换要求只是图像的位置发生变换，而像素值不会变换。几何变换的作用有很多，比如在深度学习中，如果训练集的数量不足，那么可以通过几何变换的方式来扩充训练集；在一些图像看起来“别扭”时，通过几何变换可以更“正常”。

2、几何变换的常用解决思路——伪算法

根据空间变换映射关系，确定变换后图像的大小        // 有些几何变换可能改变行列数

计算逆变换

逐行扫描目标图像g(x1,y1)
for(int i=0;i

3、几何变换方法

3.1、图像的平移变换

        图像的平移主要是对图像进行横坐标和纵坐标方向的移动，首先来讲理论基础：

        我们把图像作为一个矩阵，那么如果对一个矩阵中的元素进行平移，即需要对矩阵进行变换。在《线性代数》中我们学过，对一个矩阵的变换，实际上就是对矩阵的行列进行变换，实现这种变换只需要乘以一个变换矩阵即可。

假设我们有一个原始图像 I(x0,y0)，然后做平移变换后的图像为 I1(x1,y1)。则平移变换关系如下：

                                                                             

                                                                             

其中，Tx，Ty 分别为在 x 方向移动的距离和在 y 方向移动的距离。表示为矩阵的形式：

其实我们可以分析一下这个变换，以后也可以直接按照这种思想来分析。之前讲的点变换，实际上计算的数值是像素，而不是位置坐标，这里比较容易混起来。

先看等式右边，[x0,y0,1] 实际上是第 1 通道，也就是红色的 （ x0, y0 ）位置处的像素灰度值。注意这里是指 [x0,y0,1]这个整体的意义。通过矩阵的运算就可以知道：

x1 = x0 * 1 + y0 * 0 + 1 * Tx  = x0+Tx;            % 其实就是 x0 向 x 方向移动 Tx 

y1 = x0 * 0 + y0 * 1  +  Ty * 1 = y0 + Ty;          % 其实就是 y0 向 y 方向移动了 Ty

最后一个是通道，不变。其实后面所有的都和这个计算是类似的，都是数学中的坐标变换问题，自己画一画坐标系也可以理解。

其逆变换为：

x1 = x0 * 1 + y0 * 0 - 1 * Tx  = x0 + Tx;           % 其实就是 x0 向 x 负方向移动 Tx 

y1 = x0 * 0 + y0 * 1  -  Ty * 1 = y0 + Ty;          % 其实就是 y0 向 y 负方向移动了 Ty

 

同样，在MATLAB中，你可以用一个遍历，对所有像素进行这样的操作即可，当然，MATLAB中也可能有相关的函数吧。

3.2 图像的镜像

        镜像变换主要分为水平镜像和竖直镜像两种，这里我们并不直接给定方程，而是通过自己的理解和上面讲的进行推导（让我们来体验学习真正的快乐）：

首先：我们需要理解图像的水平镜像，还是用图片来看比较直观。

实际上这幅图就是用镜像处理后拼接在一起的。那么假设我们有一个图像，也就是有个大一些的矩阵，我们怎么让矩阵左右两边的元素互换位置？用代数来讲，这个问题就是我现在有个水平方向 m 个元素，竖直方向 n 个元素的 m*n 矩阵，然后我想让这个矩阵数值方向不变，然后让水平方向镜像。

首先，需要找到镜像用的对称轴，其实对称轴好找，就是左右边缘嘛！

其次，我们知道高中学物理的时候，镜像的对应点距离对称轴的距离是相等的。 那么，我们以对称轴作为 y 轴，因为只做这个方向的对称，所以不考虑 x 轴。那么我们知道，实际位置的对应关系是 [x0,y0,1]  的关于 y 镜像值 为 [-x0,y0,1]。即：

然后可以转化为下述问题： 

也就是我们最终要求的就是这个3*3矩阵A ，熟悉线代的都知道，这个就是个矩阵初等变换，也就是说是对第一个元素取负数。那么有：

        但是这个矩阵 A3*3 在图像处理中是有问题的，因为在图像中坐标用于描述位置信息，你最终的像素还要放在原来图像的像素位置上。就相当于你把要做镜像的图像抠出来，留下了很多小的像素坑，要填入的就是镜像后的数据。那么这样是不应该存在负数的。所以要把这个负数处理一下。我们知道当填图的时候如果出现负数，其实也可以理解为反方向填，我们可以把 第 i 个位置本来应该填的数据填成 width - i 处的元素。这个width就是我们可以通过 MATLAB 的size函数得到图像的宽度。

这时有：

则矩阵 A3*3 就出来了：

因此，我们可以遍历图像，对每一处都乘矩阵 A33 即可。

由此看来，其实想要做好数字图像处理，线性代数和矩阵论是必不可少的知识（其实数学真的对人类社会尤其是科学技术很重要，所以研究一定要有数学思维！——自己瞎总结的）。

然后直接给出图像竖直镜像变换的矩阵：

把矩阵代入到伪算法里面就是后面要实现的工作了，这里就不具体放代码了。

3.3 图像的转置

        转置运算是线性代数中常用的一种计算方式，简单地说就是行变列，列变行。在MATLAB中用一个撇就能实现（感觉不由自主就会朝着数学分析上面去）。

 变换矩阵：

 

3.4 图像的缩放

        需要不断强调的问题是：图像的几何变换是对矩阵的行数据和列数据进行操作，而不是直接对像素进行操作。区别是对像素的操作的效果是图像的颜色变化、亮度变化、对比度变化等视觉感受；而对行列操作则会改变图像的大小、是否倾斜（旋转）、是否镜像等，而不会影响像素的值大小。

        图像的缩放本质上也是对图像宽高乘一个系数，别看什么比例因子之类的，其实就是为了发论文的时候显得高大上，实际上就是个取值范围在(0,r]之间的值，这个 r 可以看作很大的数，但是他是有限的，这里面取了个半开半闭区间，就是一般不考虑0。我们知道，一个正数值，乘大于 1 的值就会对其有放大作用，乘一个 0 到 1 之间的数会使它缩小。图像处理也是这样。图像的缩放在数学上可以表示为：

转换矩阵为: