OCR识别:纸币(人民币)号码识别
随着近几年支付宝、微信等非现支付手段的兴起,现金支付好像离我们的生活越来越远,笔者现在出门基本不带钱包,凭着手机就可以走遍全中国,尤其笔者目前从事支付宝和微信推广刷脸支付方面的工作,感觉若干年后真的如马云所说,手机都可以不要了。笔者从2011研究生毕业到2015年都是在从事嵌入式终端的纸币研究的工作,比如纸币的面额识别、纸币的新旧、残损识别以及号码识别等。笔者借着2019年新版人民币的发行就自己的纸币方面研究的工作做些总结,以及就传统图像处理的方法和目前比较火的深度学习做些思考。
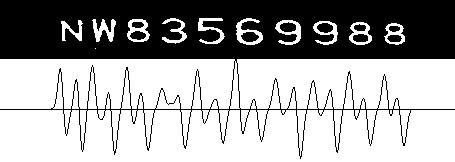
纸币鉴伪和识别设备特点是速度快,基本上20ms左右的时间处理完一张纸币4幅图像并得到结果。如下图所示:

处理设备的CPU一般是DSP或者arm等嵌入式芯片,目前一些高大上的深度学习方面的算法很难达到实时性,致力于在嵌入式终端上实现机器学习算法的实时性是笔者今后努力的方向。下面就针对人民币上的号码(冠字号码)识别运用到的一些传统方法做些介绍。

上图是经过一些预处理得到的冠字号码的图像,这些预处理的步骤后面会和大家分享,不再这次的分享范围内。要对上面的冠字号码图像进行识别,第一步就要进行分割处理,步骤如下:
1、二值化

2、采用投影法进行分割处理
1)通过计算冠字号码区域图像的水平投影,得到其水平梯度投影矩阵,确定字符的上边界和下边界。通过扫描,得到一个最小值的位置和一个最大值的位置,即分别对应冠字号码区域图像中字符的上下边界。字符图像的高度。因为在冠字号码区域图像中每个字符的高度都基本一致,通过其水平投影梯度能很好确定它们的上下边界。如图所示:

2)在确定冠字号码区域图像中字符的上下边界后,通过计算其垂直投影来确定每个字符的左右边界,具体过程如下:
-
根据计算得到的垂直投影梯度,确定10个字符的整体宽度。扫描两次,第一次从左到右,得到第一个波峰的位置,即整个字符的左边界;第二次从右到左,得到第一个波谷的位置,即整个字符的右边界。整个字符图像的宽度。如图所示:
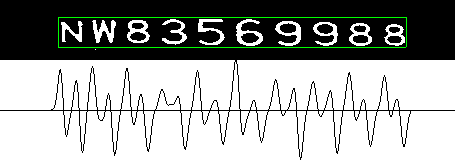
-
计算冠字号码区域图像的垂直投影,得到其垂直梯度矩阵,如图所示:
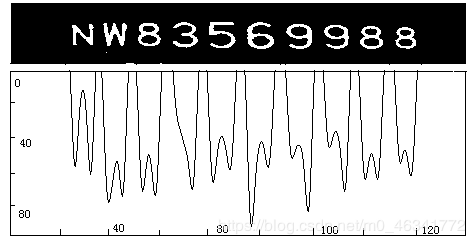
从左到右扫描 T 1 T1 T1中的值,遇到第一处值小于 t h r e s h 0 thresh0 thresh0投影标记为 t 1 a t_{1a} t1a ,继续扫描,遇到值大于 t h r e s h 0 thresh0 thresh0投影标记为 t 1 b t_{1b} t1b,接下来如果在遇到用值小于 t h r e s h 0 thresh0 thresh0投影标记为 t 2 a t_{2a} t2a,遇到大于 t h r e s h 0 thresh0 thresh0投影标记为 t 2 b t_{2b} t2b,以此类推,知道扫描结束,这样每处值为 t h r e s h 0 thresh0 thresh0的两侧都有标记对: ( t 1 a , t 1 b ) , ( t 2 a , t 2 b ) , . . . ( t n a , t n b ) (t_{1a}, t_{1b}),(t_{2a}, t_{2b}),...(t_{na}, t_{nb}) (t1a,t1b),(t2a,t2b),...(tna,tnb);从右到左以此统计每队标记 ( t i a , t i b ) (t_{ia},t_{ib}) (tia,tib)之间的像素间隔 P i P_i Pi,如果 P i > t h r e s h 1 P_i > thresh1 Pi>thresh1,这对标记之间为字符,将其切割出来,否则,是无效标记。其中 t h r e s h 0 thresh0 thresh0为通过大量实验一个统计值,这里为20。由式下面公式得到:
t h r e s h 1 = w i d t h / 20 thresh1 = width/20 thresh1=width/20
计这样计算出十个字符的左右边界,如图下面两幅图:


![]()
![]()
分割出小字符图像后要进行归一化处理,这一步比较简单,就不讨论了,接下来就要对每个字符图像提取特征,笔者采用的是提取字符图像梯度特征作为统计特征.其特征提取步骤如下:
1)求归一化后的字符图像分别在X轴方向和Y轴方向的梯度向量。系统在计算图像在X轴方向和Y轴方向的梯度向量时,可以用Soble和Roberts等算子,这里选用Soble算子。X轴方向和Y轴方向的Soble算子如图所示。
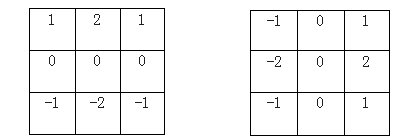
点 ( x , y ) (x,y) (x,y)处的梯度向量 g ( x , y ) = [ g x , g y ] T g(x,y)=[g_x,g_y]^T g(x,y)=[gx,gy]T,其中
g x ( x , y ) = f ( x + 1 , y − 1 ) + 2 f ( x + 1 , y ) + f ( x + 1 , y + 1 ) − f ( x − 1 , y − 1 ) − 2 f ( x − 1 , y ) + f ( x − 1 , y + 1 ) g_x(x,y) = {f(x+1,y-1)+2f(x+1,y)+f(x+1,y+1)} -f(x-1,y-1)-2f(x-1,y)+f(x-1,y+1) gx(x,y)=f(x+1,y−1)+2f(x+1,y)+f(x+1,y+1)−f(x−1,y−1)−2f(x−1,y)+f(x−1,y+1)
g y ( x , y ) = f ( x − 1 , y + 1 ) + 2 f ( x , y + 1 ) + f ( x + 1 , y + 1 ) − f ( x − 1 , y − 1 ) − 2 f ( x , y − 1 ) + f ( x + 1 , y − 1 ) g_y(x,y) = f(x-1,y+1)+2f(x,y+1)+f(x+1,y+1)-f(x-1,y-1)-2f(x,y-1)+f(x+1,y-1) gy(x,y)=f(x−1,y+1)+2f(x,y+1)+f(x+1,y+1)−f(x−1,y−1)−2f(x,y−1)+f(x+1,y−1)
- 根据上面得到的字符图像每个像素的梯度向量 g ( x , y ) = [ g x , g y ] T g(x,y)=[g_x,g_y]^T g(x,y)=[gx,gy]T,把该向量分解到下图所示的八个方向上,并用分别记录每像素的梯度向量在各个方向的分解值,构成8个梯度子图。
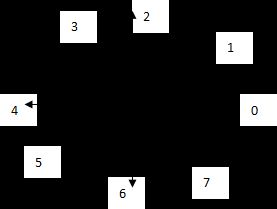
梯度向量的具体分解过程如下:将字符图像中的每个点的的梯度向量分解到上面八个方向中,分解如图所示。
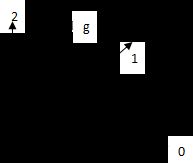
这样我们就可以得到字符图像八个方向的梯度图像,字符归一化处理后,大小为40x24,所以梯度图像的大小也是40x24。
3)将每个梯度图像分解为15个5x3的小块,这样就可以得到120个5x3的小块梯度图像,我们对每个一小块梯度图像用高斯模块进行处理,得到这一小块梯度图像的梯度特征,所以最后我们对每个字符图像提取了120维梯度特征。
最后是基于最小距离对字符进行识别,其基本思想是,将提取的字符特征向量和模板中的字符的特征向量进行匹配运算,然后得到这两个向量之间的距离,最后把这些距离从大到下进行排列,去距离最小的为待识别字符所属的字符类别。本系统中采用的欧式距离。假如总的为 m m m,各类中的特征向量为 Z 1 , Z 2 . . . . Z m Z_1,Z_2....Z_m Z1,Z2....Zm。则由中提取的特征向量 X X X与之间的可由下式定义:
D i = ( X − Z i ) T ( X − Z i ) D_i=\sqrt{(X-Z_i)^T(X-Z_i)} Di=(X−Zi)T(X−Zi)
通过计算,我们将得到距离结果 D 1 , D 2 , . . . , D m D_1,D_2,...,D_m D1,D2,...,Dm,在这 m m m个结果中选取最小值为待识别的字符判定归为最接的向量 Z k Z_k Zk所的类别 w k w_k wk。
结尾
以上是笔者对过去纸币方面号码识别方面工作的一些总结,这些方法放在现在也是不是那么的高大上,但是他简单实用,就目前的情况来看,传统的图像处理方法在一些领域(特别是嵌入式方面)还是发挥比较重要的作用,但我们也要紧跟时代的步伐,要学习和掌握机器学习方面的知识和应用,笔者目前正在研究自取柜方面的工作,说的通俗点就是识别饮料瓶,笔者有一些样本数据,大家如果感兴趣可以一起探讨学习。
![]()
扫描上方二维码关注“嵌入式案例Show”公众号,看更多嵌入式案例