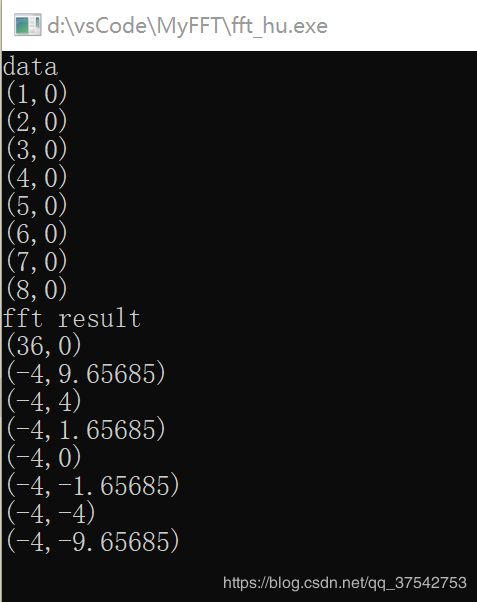
快速傅里叶变换（研二的我终于弄懂了）

研二的我仍然对快速傅里叶变换一知半解，于是乎，本着待在家里，能耗时间就多耗点，不知道何年马月我才可以在外面快乐的奔跑~~

---

快速傅里叶变换的实现（c++版本）

在做项目的时候，需要用到matlab里的fft，移植到c++时，结果有点出入，于是乎，老板下令给我搞清楚！

csdn上的这篇文章很友好，从数学多项式的角度解释了傅里叶变换的含义（傅里叶变换就是求多项式的点值表达式）；But，代码部分我看的有些迷茫，可能这就是菜吧 ；本着无聊消耗时间的心，我决定要弄出个所以然，造福之后的小可爱们
二进制的翻转

void bitReverse(int bitNum,int *position)
{
    int len=1<<bitNum;
    for(int i=0;i<len;++i)
    {
        position[i]=(position[i>>1]>>1)|((1&i)<<(bitNum-1));
    }
}

 position[i]=(position[i>>1]>>1)|((1&i)<<(bitNum-1));

上面这个地方是困扰我时间最长的地方，那么多位的左移右移究竟是个嘛意思？后来在这篇文章里面弄懂了

这里是在计算position [i] 的时候，认为position [i-1] 的翻转已经计算完毕，并且存储在position [i-1]；

计算position [i] ，把前i-1位和最后一位作为两部分进行处理，把最后一位挪到开头，然后在后面接上前i-1位的翻转；

fft变换

void fft(cp *a, int *rev,int n, int flag)
{
    for (int i = 0; i < n; i++)
    {
        //i小于rev[i]时才交换，防止同一个元素交换两次，回到它原来的位置。
        if (i < rev[i])
            swap(a[i], a[rev[i]]);
    }
    for (int h = 1; h < n; h *= 2) //h是准备合并序列的长度的二分之一
    {
        cp wn = exp(cp(0, flag * -1 * pie / h)); //求单位根w_n^1
        for (int j = 0; j < n; j += h * 2)       //j表示合并到了哪一个序列
        {
            cp w(1, 0);
            for (int k = j; k < j + h; k++) //k表示合并到了序列里的哪一位
            {
                cp x = a[k];
                cp y = w * a[k + h];
                a[k] = x + y; //这两步是蝴蝶变换
                a[k + h] = x - y;
                w *= wn; //求w_n^k
            }
        }

        //判断是否是FFT还是IFFT
        if (flag == -1)
            for (int i = 0; i < n; i++)
                a[i] /= n;
    }
}

cp wn = exp(cp(0, flag * -1 * pie / h)); //求单位根w_n^1

1 在这一块代码里面，困扰我比较久的是这里的单位根，文章里面没有加负号，算出的结果也就无法和matlab的结果匹配；后来我查阅文章，原来信号处理里面的旋转因子是有负号的
$w_n^k=e^{-j2pik/N}$

2 h,j,k的含义；
h表示将要合并序列的长度的一半
j是序列的个数
k是序列中合并到了哪一位

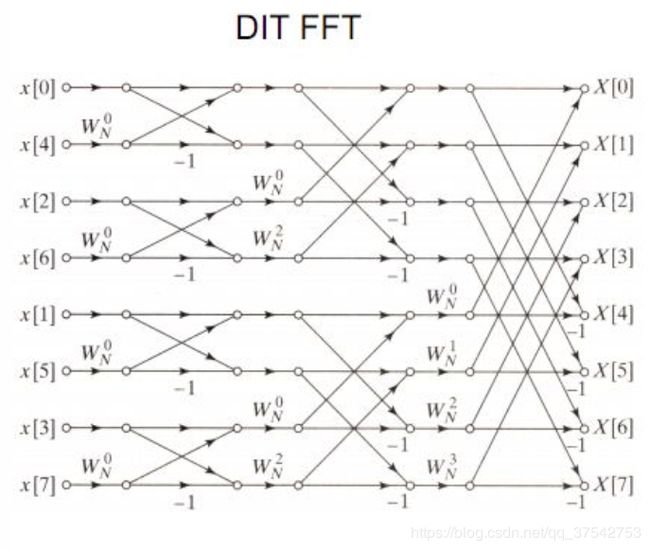
比如N=8,8点fft，一共处理三轮得到最终的结果；
第一轮有4个2点的fft序列 h=1; j=0,1,2,3; k=0;
第二轮有2个4点的fft序列 h=2; j=0,1 ; k=0,1;
第三轮有1个8点的fft序列 h=4; j=0 ; k=0,1,2,3;

结果验证：

MATLAB 结果：

附上完整代码：

#include  //万能的头文件，包含了常用的头文件
using namespace std;
typedef complex<double> cp;
const double pie = acos(-1); //很巧妙的一种定义pi的方式
//1.将最终的位置确定出来，二进制翻转
//2.fft变换

//1.将最终的位置确定出来，二进制翻转
void bitReverse(int bitNum, int *position)
{
    int len = 1 << bitNum;
    for (int i = 0; i < len; ++i)
    {
        position[i] = (position[i >> 1] >> 1) | ((1 & i) << (bitNum - 1));
    }
}

//2.fft变换
void fft(cp *a, int *rev,int n, int flag)
{
    for (int i = 0; i < n; i++)
    {
        //i小于rev[i]时才交换，防止同一个元素交换两次，回到它原来的位置。
        if (i < rev[i])
            swap(a[i], a[rev[i]]);
    }
    for (int h = 1; h < n; h *= 2) //h是准备合并序列的长度的二分之一
    {
        cp wn = exp(cp(0, flag * -1 * pie / h)); //求单位根w_n^1
        for (int j = 0; j < n; j += h * 2)       //j表示合并到了哪一个序列
        {
            cp w(1, 0);
            for (int k = j; k < j + h; k++) //k表示合并到了序列里的哪一位
            {
                cp x = a[k];
                cp y = w * a[k + h];
                a[k] = x + y; //这两步是蝴蝶变换
                a[k + h] = x - y;
                w *= wn; //求w_n^k
            }
        }
        //判断是否是FFT还是IFFT
        if (flag == -1)
            for (int i = 0; i < n; i++)
                a[i] /= n;
    }
}

int main()
{
    int length = 8;                     
    int bit_len = log(length) / log(2); 
    int *Position = new int[length]();
    bitReverse(bit_len, Position); 
    cp *data = new cp[length]();
    for (int i = 0; i < 8; ++i)
        data[i] = i + 1;
    cout << "data" << endl;
    for (int i = 0; i < 8; ++i)
        cout << data[i] << endl;
    fft(data,Position,length,1);
    cout << "fft result" << endl;
    for (int i = 0; i < 8; ++i)
    cout << data[i] << endl;
    delete Position;
    return 0;
}

总结：

花了几天时间，终于对自己有了一个交代，感慨万千，原本应该大学里就弄懂的知识一拖再拖，拖到了现在；这也让我更加崇拜那些学霸们，他们三下五除二就弄懂的知识在我这个菜鸡面前是座大山，不过好在我已经翻过去了，多的不说，继续加油吧！
(｡◕ˇ∀ˇ◕)
附上菜鸡这几天的草稿纸