数理统计-ML-CV知识点(正在更新中)
数理统计-ML-CV知识点
- 路过图床的外链要用第一个详细的链接,否则会掉链。
<–>
1、非端到端
非端到端的学习则是分阶段处理,每个阶段都是一个独立的模块,相互不干扰。
传统机器学习的流程往往由多个独立的模块组成,比如在一个典型的自然语言处理(Natural Language Processing)问题中,包括分词、词性标注、句法分析、语义分析等多个独立步骤,每个步骤是一个独立的任务,其结果的好坏会影响到下一步骤,从而影响整个训练的结果,这是非端到端的。
2、端到端
端到端的学习旨在通过一个深度神经网络直接学习从数据的原始形式到数据的标记的映射,没有proposal region。其中从输入端到输出端会得到一个预测结果,将预测结果和真实结果进行比较得到误差,将误差反向传播到网络的各个层之中,调整网络的权重和参数直到模型收敛或者达到预期的效果为止,中间所有的操作都包含在神经网络内部,不再分成多个模块处理。由原始数据输入,到结果输出,从输入端到输出端,中间的神经网络自成一体(也可以当做黑盒子看待),这是端到端的。
两者相比,端到端的学习省去了在每一个独立学习任务执行之前所做的数据标注。
3、高斯分布(正态分布)
数学期望为μ的Normal分布
X ∼ N ( μ , σ 2 ) X \sim N\left(\mu, \sigma^{2}\right) X∼N(μ,σ2)
概率密度函数为:
f ( x ) = 1 σ 2 π e − ( x − μ ) 2 2 σ 2 f(x)=\frac{1}{\sigma \sqrt{2 \pi}} e^{-\frac{(x-\mu)^{2}}{2 \sigma^{2}}} f(x)=σ2π1e−2σ2(x−μ)2
4、最大似然估计
已知发生的结果,求之前的概率大小
伯努利分布(两点分布)如下:
f ( x ; p ) = { p i f x = 1 1 − p i f x = 0 f(x;p)= \begin{cases} p \qquad\ if \quad x=1 \\ 1-p \quad if \quad x=0 \end{cases} f(x;p)={p ifx=11−pifx=0
也可写成:
f ( x ; p ) = p x ( 1 − p ) 1 − x for x ∈ { 0 , 1 } f(x ; p)=p^{x}(1-p)^{1-x} \quad \text { for } x \in\{0,1\} f(x;p)=px(1−p)1−x for x∈{0,1}
多个独立事件的似然函数:
L = ∏ i = 1 N p i \mathcal{L}=\prod_{i=1}^{N} p_{i} L=i=1∏Npi
对多项乘积的求导往往非常复杂,但是对于多项求和的求导却要简单的多,对数函数不改变原函数的单调性和极值位置,而且根据对数函数的性质可以将乘积转换为加减式,这可以大大简化求导的过程:
log ( L ) = log ( ∏ i = 1 N p i ) = ∑ i = 1 N log ( p i ) \log (\mathcal{L})=\log \left(\prod_{i=1}^{N} p_{i}\right)=\sum_{i=1}^{N} \log \left(p_{i}\right) log(L)=log(i=1∏Npi)=i=1∑Nlog(pi)
似然函数的最大值
似然函数的最大值意味着什么?让我们回到概率和似然的定义,概率描述的是在一定条件下某个事件发生的可能性,概率越大说明这件事情越可能会发生;而似然描述的是结果已知的情况下,该事件在不同条件下发生的可能性,似然函数的值越大说明该事件在对应的条件下发生的可能性越大。
可知最大似然估计的一般求解过程:
(1) 写出似然函数;
(2) 对似然函数取对数,并整理;
(3) 求导数;
(4) 解似然方程,令其等于0的解,能使产生这些已知数据的概率最大。
5. Logit模型
Odds指的是事件发生的概率与事件不发生的概率之比:
Odds = Probability of event Probability of no event = P 1 − P \text {Odds}=\frac{\text {Probability of event}}{\text {Probability of no event}}=\frac{P}{1-P} Odds=Probability of no eventProbability of event=1−PP
概率P的变化范围是[0,1],而Odds的变化范围是[0,+∞)。再进一步,如果对Odds取自然对数,就可以将概率P从范围[0,1 ]映射到(-∞,+∞)。Odds的对数称之为Logit。

与概率不同,Logit的一个很重要的特性就是没有上下限——这就给建模带来极大方便
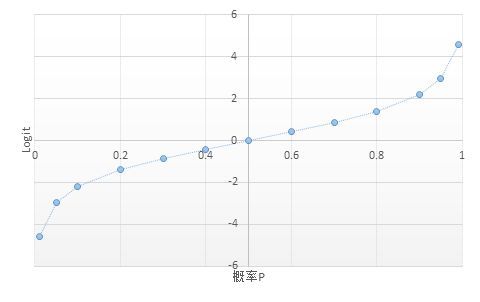
由于 Logit 和
( β 0 + β 1 X ) \left(\beta_{0}+\beta_{1} X\right) (β0+β1X)
都是在(-∞,+∞)上变化,我们可以尝试建立Logit 和 ( β 0 + β 1 X ) \left(\beta_{0}+\beta_{1} X\right) (β0+β1X)之间的对应关系。
log i t ( P i ) = β 0 + β X \log i t\left(P_{i}\right)=\beta_{0}+\beta X logit(Pi)=β0+βX
如果将β和X看成向量形式,则
log i t ( P i ) = ln P i 1 − P i = β 0 + β 1 x 1 , i + β 2 x 2 , i + ⋯ + β n x n , i \log i t\left(P_{i}\right)=\ln \frac{P_{i}}{1-P_{i}}=\beta_{0}+\beta_{1} x_{1, i}+\beta_{2} x_{2, i}+\cdots+\beta_{n} x_{n, i} logit(Pi)=ln1−PiPi=β0+β1x1,i+β2x2,i+⋯+βnxn,i
上式正是二项Logit模型的基本形式。
6. NMS
NMS在物体检测中的应用
物体检测中应用NMS算法的主要目的是消除多余(交叉重复)的窗口,找到最佳物体检测位置。
7. 贝叶斯公式
后验概率=先验概率*似然概率
P ( A ∣ B ) = P ( A ) P ( B ∣ A ) P ( B ) P(A|B)=P(A) \frac{P(B|A)}{P(B)} P(A∣B)=P(A)P(B)P(B∣A)
用条件概率,看起来更加直白:
P ( A ∣ B ) = P ( A ∩ B ) / P ( B ) P (A|B)=P(A \cap B ) / P(B) P(A∣B)=P(A∩B)/P(B)
贝叶斯公式表明,在知道A发生的条件下,Bi的概率密度分布:
P ( B i ∣ A ) = P ( B i ) P ( A ∣ B i ) ∑ j = 1 n P ( B j ) P ( A ∣ B j ) P(B_{i}|A)= \frac{P(B_{i})P(A|B_{i})}{ \sum _{j=1}^{n}P(B_{j})P(A|B_{j})} P(Bi∣A)=∑j=1nP(Bj)P(A∣Bj)P(Bi)P(A∣Bi)
写成积分形式,其中π指的是参数的概率分布,$ \pi ( \theta |x) 指 的 是 先 验 概 率 , T ( l x ) 指 的 是 后 验 概 率 , 指 的 是 我 们 观 测 到 的 样 本 的 分 布 , 也 就 是 似 然 函 数 ( l i k e l i h o o d ) , 记 住 竖 线 ∣ 左 边 的 才 是 我 们 需 要 的 。 其 中 积 分 求 的 区 间 O 指 的 是 参 数 0 所 有 可 能 取 到 的 值 的 域 , 所 以 可 以 看 出 后 验 概 率 指的是先验概率,T(lx)指的是后验概率,指的是我们观测到的样本的分布,也就是似然函数(likelihood),记住竖线|左边的才是我们需要的。其中积分求的区间O指的是参数0所有可能取到的值的域,所以可以看出后验概率 指的是先验概率,T(lx)指的是后验概率,指的是我们观测到的样本的分布,也就是似然函数(likelihood),记住竖线∣左边的才是我们需要的。其中积分求的区间O指的是参数0所有可能取到的值的域,所以可以看出后验概率 \pi ( \theta |x) $是在知道X的前提下在O域内的一个关于0的概率密度分布,每一个0都有一个对应的可能性(也就是概率)。
π ( θ ∣ x ) = f ( x ∣ θ ) π ( θ ) ∫ θ f ( x ∣ θ ) π ( θ ) d θ \pi ( \theta |x)= \frac{f(x| \theta ) \pi ( \theta )}{ \int _{ \theta }f(x| \theta ) \pi ( \theta )d \theta } π(θ∣x)=∫θf(x∣θ)π(θ)dθf(x∣θ)π(θ)
8. 排列数
从n个不同元素中任取m(m≤n)个元素,按照一定的顺序排列起来,叫做从n个不同元素中取出m个元素的一个排列。当m=n时所有的排列情况叫全排列。
排列数公式:
可分为m个步骤:
第1步,第1位可以从n个元素中任选一个填上,共有n种填法;
第2步,第2位只能从余下的n-1个元素中任选一个填上,共有n-1种填法;
第3步,第3位只能从余下的n-2个元素中任选一个填上,共有n-2种填法;
……
第m步,当前面的m-1个空位都填上后,第m位只能从余下的n-(m-1)个元素中任选一个填上,共有n-m+1种填法。
根据分步计数原理,全部填满m个空位共有n(n-1)(n-2)…(n-m+1)种填法。所以得到公式:
A n m = n ( n − 1 ) ( n − 2 ) ⋯ ( n − m + 1 ) = n ! ( n − m ) ! A_{n}^{m} =n(n-1)(n-2) \cdots (n-m+1)= \frac{n!}{(n-m)!} Anm=n(n−1)(n−2)⋯(n−m+1)=(n−m)!n!
全排列数公式:
f ( n ) = n ! ( 0 ! = 1 ) f(n)=n!(0!=1) f(n)=n!(0!=1)
9. 组合数
从n个不同元素中,任取m(m≤n)个元素并成一组,叫做从n个不同元素中取出m个元素的一个组合;从n个不同元素中取出m(m≤n)个元素的所有组合的个数,叫做从n个不同元素中取出m个元素的组合数。
