Computer Vision（C. Rasche）计算机视觉 论文解读（3 Image Processing I: Scale Space, Pyramid and Gradient Image）

目录

3 Image Processing I: Scale Space, Pyramid and Gradient Image

3.1 Scale Space

3.2 Pyramid

3.3 Gradient Image

3.4 Exercises

---

3 Image Processing I: Scale Space, Pyramid and Gradient Image

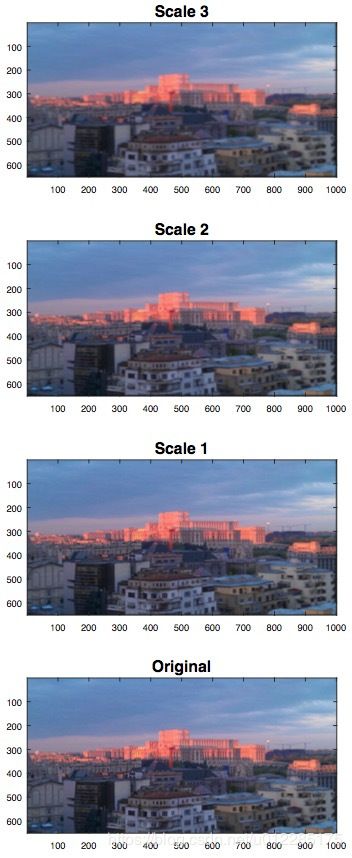
对于许多计算机视觉任务，模糊图像并分别分析这些不同的模糊是有用的。 我们已经在上一节中介绍了模糊图像的概念，但是在这里我们重复产生这种模糊，增加的滤波器尺寸到达所谓的比例空间，如图4所示。这个空间将在随后的部分介绍3.1。 然后我们介绍图像金字塔，第3.2节，粗略地说 - 缩小了尺度空间。

 图4：图像的缩放空间。 从底部到顶部观察增加的模糊。

Original: 未经过滤的图像。

Scale 1: 使用高斯滤波器sigma等于1，来平滑。

Scale 2: 使用高斯滤波器来平滑。

Scale 3: 使用高斯滤波器来平滑。

它被称为空间，因为可以将其视为三维空间，第三维对应于具有变量的细到粗轴。
在较粗的尺度（较大的值）下，更容易找到整体的轮廓和区域，但结构有时会被其他不同的结构所污染。 通常对较粗糙的尺度进行下采样以获得更紧凑的尺度空间表示，从而形成金字塔，参见图5.附录I.2中的代码。

(在这种情况下，分别对每个颜色通道执行滤波，一次用于红色，一次用于绿色，一次用于蓝色图像）

对于许多计算，知道强度景观如何在每个像素处“定向”也是有用的。 具体来说，我们想知道小像素邻域的每个图像像素的“表面斜率”。 这用梯度图像表示，将在3.3节中解释。

3.1 Scale Space

通过将图像与在小邻域中平均的二维滤波器进行卷积来使图像模糊。 在上一节的介绍性示例中，我们仅使用了求和函数，但通常使用高斯滤波器完成图像模糊，就像我们滤波面部轮廓一样（第2.2节）。 这里高斯滤波器是一个二维函数，看起来如图9的前四个补丁所示。它表示为，其中x和y是图像轴，其中是调节模糊量的标准差- 也称为平滑参数。 在信号处理的语言中，将模糊处理表示为卷积，由星号表示。有人说，图像由滤波器进行卷积

                                                         (2)

导致更粗糙的图像。如果您不熟悉2D卷积过程，请立即阅读附录B.2以熟悉它。

如果重复进行这种模糊，则图像变得越来越粗糙，相应的强度景观变得更加平滑，如图4所示。实际上，有不同的方式到达尺度空间。 最直接的实现是使用尺寸增大的2D高斯重复低通滤波原始图像，首先使用，然后使用等。然而，这种方法有点慢并且存在快速实现，为此我们参考附录B.2。

得到的图像堆栈，，称为尺度空间。 在尺度空间的典型图示中，底部图像对应于原始图像; 随后的较高图像对应于较粗略的图像。 换句话说，图像从底部到顶部垂直对齐，并且可以将该对齐视为细到粗轴。 该轴现已标记为。 然后将得到的空间表示为

                                                                                        (3)

轴可以理解为平滑变量：等于零的值对应于原始图像，即，没有平滑; 值等于1对应于第一粗略图像等。在应用中，sigma值通常在1到5之间，。

Application 尺度空间特别用于以下特征检测过程：

1. 区域发现：我们可以通过相互减去尺度来轻松确定更亮和更暗的区域，这是我们将在4.1节中返回的技术。
2. 跨越尺度（轴）的结构的验证：例如，如果可以在不同尺度上找到特定特征，则不太可能是偶然的，这是一种通常用于特征检测的技术（第6节）。
3. 寻找更多“连贯性”：例如，轮廓在较粗糙的尺度上看起来更连续（第4.2节）。

在Matlab中，我们可以使用函数fspecial创建高斯滤波器，并使用命令conv2对图像进行卷积：

Fsc1 = fspecial(’gaussian’, [3 3], 1); % 2D gaussian with sigma=1
Fsc2 = fspecial(’gaussian’, [5 5], 2); % 2D gaussian with sigma=2
Isc1 = conv2(Io, Fsc1, ’same’);        % filtering at scale=1

图像处理工具箱还提供诸如imgaussfilt和imfilter之类的命令来生成图像模糊，并且可能是首选功能，因为它们针对速度进行了优化。

在Python中，子模块scipy.ndimage包含用于模糊图像的函数gaussian_filter：

scipy.ndimage.gaussian_filter(I, sigma=1.0)

生成这样的尺度空间为我们提供了更多信息，我们打算利用这些信息来改进我们的特征提取。 然而，这种信息增益是以更多内存使用为代价的，因为我们现在拥有多个图像。 并且多个图像在搜索特征时意味着更多的计算。 但是我们可以通过“压缩”粗尺度来减少这种尺度空间，而不会造成太多信息损失，从而导致在下一节中处理金字塔。

 

图5：图像的多分辨率金字塔。 尺度空间的图像（图4）每隔一个像素进行一次下采样：每个刻度沿着细到粗轴的分辨率减半。

Original: 原始

Level 1: 的子采样

Level 2: 的子采样

Level 3: 的子采样

它被称为金字塔，因为人们可以对齐图像，使它们形成金字塔 - 为简单起见，我们在正面显示图像。

3.2 Pyramid

使用整个尺度空间S进行操作在计算上是昂贵的，因为它相当大并且在某种程度上是多余的。 因为较粗的尺度不再具有任何精细结构，所以对它们进行二次采样是有意义的：对于每个新的较粗的尺度，仅沿着水平轴并且沿着垂直轴每秒拍摄一个像素。 我们如此到达到级别的（八度）金字塔，参见图5。在更高级别的语言中，我们可以通过选择每隔一行和每列来“手动”下采样，即使用以下方式对采样行进行子采样：

Idwn = Isc1(1:2:end,:); % sub-sampling rows

接下来是子采样列：

Idwn = Idwn(:,1:2:end); % sub-sampling columns

在Matlab中还存在函数downsample，但是它仅适用于行 - 如果输入是矩阵; 然后我们需要翻转矩阵以沿着列对其进行下采样。 Matlab还提供函数impyramid，它既可以执行高斯滤波，也可以执行下采样。 但我们也可以操作另一个方向和上采样：

I1  = impyramid(I0,’reduce’);  % filter and downsampling every 2nd
I0  = impyramid(I1,’expand’);  % upsampling every 2nd

如果需要其他向下或向上采样步骤 - 而不是减半和加倍 - 那么函数imresize可能更方便。

Python

skimage.transform.pyramid reduce 和 .pyramid expand

Application 在许多匹配任务中，搜索从金字塔的顶层开始的模式，最小的分辨率，然后向下到底层的工作更有效，这种策略也称为粗到精搜索（或匹配））。 更具体地，仅在以粗略水平进行潜在检测之后，然后通过朝向更精细的水平开始验证，其中由于更高的分辨率，搜索更耗时。

3.3 Gradient Image

梯度图像描述了强度景观中每个点的陡度，更具体地说是景观的局部“表面”是如何倾斜的。 在每个像素处，确定两个度量：斜率的方向，也称为梯度; 斜率的大小-陡度。 因此，梯度图像由两个值的映射组成，即方向和斜率。 该信息最方便地用箭头表示，即作为矢量场，参见图6：箭头的方向对应于梯度; 箭头的长度对应于斜率。

 图6：梯度图像。 箭头指向梯度的方向 - 邻域的局部斜率; 箭头的长度对应于梯度的大小。 梯度方向指向高值（白色= 255;黑色= 0）。

（图片描绘的是什么？提示：眯起眼睛产生粗糙的比例。）

为了确定梯度，可以得到两个维度的导数，即沿两个轴的相邻像素之间的差异，分别为和。 此操作通常使用nabla符号表示，求梯度运算：

                                                                                        (4)

由此，梯度信息表示为矢量。 我们举例说明：平面上的一个点没有倾斜，因此没有大小和无关的方向 - 梯度为零; 斜率中的点具有特定方向 - 超出范围的角度值 - 以及表示陡峭度的特定斜率。 使用两个参数（atan2）使用反正切函数计算方向，在大多数软件实现中返回值。 使用毕达哥拉斯公式计算斜率。

直接在原始图像上确定梯度场通常不会返回“有用”结果，因为原始图像通常太嘈杂（不规则）。 因此，通常首先使用小的高斯函数对图像进行低通滤波，例如，在确定其梯度场之前，。

在Matlab中存在常规的imgradient，它立即返回斜率和方向（Image Processing Toolbox）; 如果后来在代码中再次需要求导，那么可以使用imgradientxy来获得对应于各个梯度的两个矩阵。 如果我们缺少工具箱，我们可以使用下面的代码片段，其中函数gradient返回两个矩阵 - 图像的大小 - 表示沿两个维度的梯度：

Fg         = fspecial(’gaussian’,[3 3],1); % 2D gaussian of size 3x3 with sigma=1
Isc1       = conv2(I, Fg, ’same’);
[Dx Dy]    = gradient(single(Isc1));       % gradient along both dimensions
Dir        = atan2(-Dy, Dx) + pi;          % [-pi,pi]
bk0        = Dir<0;                        % negative values
Dir(bk0)   = Dir(bk0)+2*pi;                % [0,2*pi]
Mag        = sqrt(Dx.^2+Dy.^2);            % gradient magnitude

在示例代码中，角度值被移动到正范围。 可以使用函数quiver绘制梯度场：

% --- Plotting:
X = 1:ISize(2);  Y = 1:ISize(1);
figure(1); clf; colormap(gray);
imagesc(I, [0 255]); hold on;
quiver(X, Y, Dx, Dy);

在Python中，我们可以用numpy模块中的gradient函数：

Dx, Dy = numpy.gradient(I)

 Applicaiton 梯度图像用于各种任务，例如边缘检测，特征检测和特征描述（即将出现）。

3.4 Exercises

我们将编写一些函数，但不是将代码立即放入单独的函数脚本中，而是首先在测试脚本中开发代码，我们称之为t_NameOfScript（t for test），因为在脚本中调试比在一个函数脚本调试简单。 一旦我们在脚本中充分开发了代码，我们就将命令复制到一个名为f_NameOfFunction的函数脚本中（函数为f）。 不要删除测试脚本中的代码 - 留在那里！ 然后，在测试脚本的末尾应用函数f_NameOfFunction来验证其输出，例如： 通过获取测试脚本中输出的差异和函数脚本的输出。

1. 编写脚本t_Pyramid，为图像生成金字塔（例如，参见附录I.2）。 将级别存储在cell或struct中。 用subplot显示金字塔。
   1. 首先了解滤波器：绘制它们并在中心观察它们的最大值。 使用colorbar绘制每个的尺度。 应用命令imagesc，限制为[0 0.15]。
   2. 仔细观察滤波后的图像。 不同级别的（强度）范围是多少？ 再次使用colorbar来说明。 值为0是什么颜色？ 什么是最大值？
   3. 仔细观察图像边界。 在边界处，不能正确应用滤波器：改为做什么？ 有什么选择？
   4. 最后，将代码放入函数f_Pyramid中。
2. 编写一个生成梯度图像的脚本t_GradImg，有关提示，请参见第3.3节。
   1. 在单独的图像（imagesc）中显示方向和斜率的地图。 使用colorbar验证范围。 斜率值在哪里最大？
   2. 现在用命令quiver(箭头)显示梯度 - 方向和斜率 - 并将输出放在图像的顶部（不要忘记hold on）。 对于大图像，可能需要很长时间 - 几秒钟 - 才能显示所有箭头。 放大结果以验证输出。 箭头朝哪个方向指向？ 在强度图像中向上，向下？ 什么测量对应箭头的长度？
   3. 最后，编写函数f_GradImg，它将图像I作为输入并返回两张地图，一个具有方向值，另一个具有斜率。 返回结构中的地图GM：GM.Dir = Dir，GM.Mag = Mag，以后使用更方便。 现在使用任何（GM.Dir（:)  -  Dir（:)）验证测试脚本末尾的函数：如果为0则可以，如果没有，那么我们可能会出错 - 尽管可能存在四舍五入的差异; 用any(sum（abs（GM.Dir(:) -  Dir(:)))> 0.1)验证。

希望本文能帮助你在计算机视觉领域走得更远，学习得更加深入!