贪心算法：集合覆盖问题

贪心算法

---

贪心算法是一种解决问题的思路：每一步选择局部最优解，最终也许不会得到最优结果，但是也会接近最优结果。
贪心算法具有以下特点：

1. 每一步选择局部最优解；
2. 并非在任何情况下行之有效；
3. 贪心算法简单易实现；

教室调度问题

---

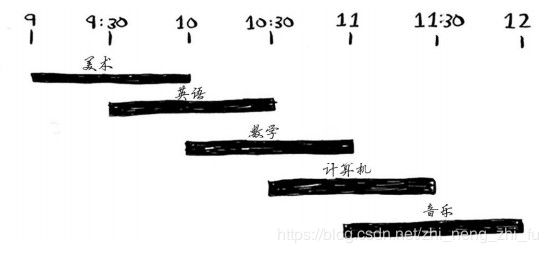
假设有如下课程表，你希望将尽可能多的课程安排在某间教室上：

课程	开始时间	休息时间
美术	9 AM	10 AM
英语	9:30 AM	10:30 AM
数学	10 AM	11 AM
计算机	10:30 AM	11:30 AM
音乐	11 AM	12 PM

你希望在这间教室上尽可能多的课。如何选出尽可能多且时间不冲突的课程呢？贪心算法的做法是：每一步选择价值回报最大的操作。具体做法如下：

• 选出结束最早的课，它就是要在这间教室上的第一堂课。
• 接下来，必须选择第一堂课结束后才开始的课。同样，你选择结束最早的课，这将是要在这间教室上的第二堂课。
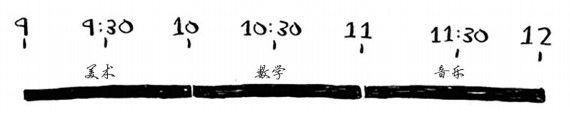
  重复这样做就能找出答案！最终选择的结果如下：

背包问题

---

假设你是个贪婪的小偷，背着可装35磅（$1磅\approx 0.45千克$）重东西的背包，在商场伺机盗窃各种可装入背包的商品。
贪心算法的策略是：

1. 盗窃可装入背包的最贵商品；
2. 再盗窃还可装入背包的最贵商品，以此类推；

以这种方式可能并不能得到最优解。有时候，你只需找到一个能够大致解决问题的算法，此时贪婪算法正好可派上用场，因为它们实现起来很容易，得到的结果又与正确结果相当接近。记住，对有些问题，可能并不存在完美的解，例如 NP 难问题。

集合覆盖问题

---

集合覆盖问题： 选择最少的集合，覆盖全部的元素。
假设你办了个广播节目，要让全美 $50$ 个州的听众都收听得到。为此，你需要决定在哪些广播台播出。在每个广播台播出都需要支付费用，因此你力图在尽可能少的广播台播出。现有广播台名单如下。

广播台	覆盖的州
(1) KONE	ID，NV，UT
(2) KTWO	WA，ID，MT
(3) KTHREE	OR，NV，CA
(4) KFOUR	NV，UT
(5) KFIVE	CA，ZA

如何找出覆盖全美 $50$ 个州的最小广播台集合呢？
最容易考虑到的可能是暴力求解法：列出每一种可能的广播集合（可能的子集有 $2^n$个）；在这些集合中选出能覆盖全美 $50$ 个州的最小集合数。假设每秒可筛选出 $10$ 个子集，其花费的时间如下：

没有任何算法可以足够快地解决这个问题！怎么办呢？使用贪婪算法可以得到非常接近的解。

1. 选出这样一个广播台，即它覆盖了最多的未被选择的州。即便这个广播台覆盖了一些已经选择的州，也没有关系；
2. 重复第一步，直到覆盖了所有的州。

贪婪算法是不错的选择，它们不仅简单，而且通常运行速度很快。在这个例子中，贪婪算法的运行时间为 $O(n^2)$，其中 $n$ 为广播台数量。

解决上述问题的代码如下：

• 第一步：准备工作：构建数据结构；
  • 用集合 states_needed 存储所有的州；
  • 用字典表示电视台 stations 的覆盖面；

states_needed = set(['mt', 'wa', 'or', 'id', 'nv', 'ut', 'ca', 'az']) # 包含要覆盖的州

stations = {} # 存储电视台集合
stations["kone"] = set(["id", "nv", "ut"])
stations["ktwo"] = set(["wa", "id", "mt"])
stations["kthree"] = set(["or", "nv", "ca"])
stations["kfour"] = set(["nv", "ut"])
stations["kfive"] = set(["ca", "az"])

final_stations = set() # 存储最终电视台的集合

• 第二步：利用贪心算法求解最少的电视台
  • 选出这样一个广播台，即它覆盖了最多的未被选择的州。我们将这个广播台存储在 best_station 中；
  • 重复第一步，直到覆盖了所有的州。

while states_needed:
    best_station = None # 最佳电视台:覆盖了最多未覆盖的州
    states_covered = set() # 最佳电视台与未覆盖州集合的交集
    for station, states in stations.items():
        covered = states_needed & states # 当前广播台与未覆盖州集合的交集
        if len(covered) > len(states_covered):
            states_covered = covered
            best_station = station
    
    states_needed -= states_covered # 更新未覆盖州的集合
    final_stations.add(best_station) # 添加贪心算法选择的电台

最终打印的结果可能如下：

print(final_stations)
# set(['ktwo', 'kthree', 'kone', 'kfive'])

暴力求解算法 和 贪心算法 求解时间对比：

NP完全问题

---

什么样的问题称为 NP 完全问题呢？ 就像集合覆盖问题一样，你需要计算所有的解，并从中选择优的解。NP 完全问题以计算量大无法求得最优解而著称，贪心策略是解决 NP 完全问题一个很重要且有效的方法。它也许不能得到最优解，但是可以得到最接近最优解的结果。

总结

---

1. 贪婪算法寻找局部最优解，企图以这种方式获得全局最优解。
2. 对于NP完全问题，还没有找到快速解决方案。
3. 面临NP完全问题时，最佳的做法是使用近似算法。
4. 贪婪算法易于实现、运行速度快，是不错的近似算法。