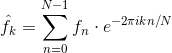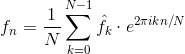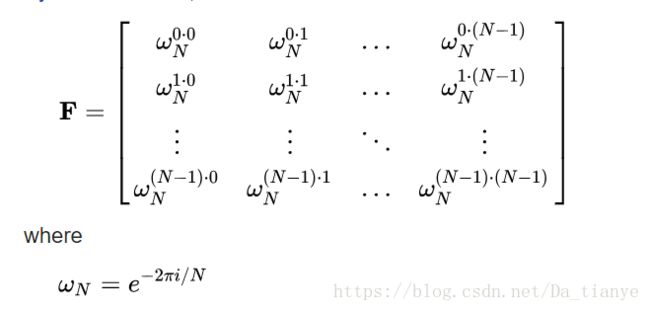长安一片月噢
长安一片月噢

The FFT Algorithm

Fourier Transform(DFT)

There is an entire theory of expanding functions in terms of sin(kwx) called Fourier Analysis. We are interested in extracting frequencies from DATA.

x_{0}, x_{1}, x_{2}, x_{3}, x_{4} ... f_{0}, f_{1}, f_{2}, f_{3}, f_{4} ...

\left \{ f_{0}, f_{1}, ..., f_{N-1} \right \}\overset{DFT}{\rightarrow} \left \{ \hat{f_{0}}, \hat{f_{1}}, ..., \hat{f_{N-1}}\right \}

\hat{f_{k}} = \sum_{n=0}^{N-1} f_{n}\cdot e^{-2\pi ikn/N}

\omega = 2\pi kn/N

\left \{ \hat{f_{0}}, \hat{f_{1}}, ..., \hat{f_{N-1}}\right \}\overset{IDFT}{\rightarrow} \left \{ f_{0}, f_{1}, ..., f_{N-1} \right \}

f_{n} =\frac{1}{N} \sum_{k=0}^{N-1}\hat{f_{k}}\cdot e^{2\pi ikn/N}

The FFT Algorithm_第1张图片

Fast Fourier Transform

A fast Fourier transform (FFT) is an algorithm that samples a signal over a period of time (or space) and divides it into its frequency components.

DFT may be implemented much more efficiently if N the # of samples is the power of 2:

 

你可能感兴趣的:(The FFT Algorithm)

  • Python算法L5：贪心算法 小熊同学哦 Python算法算法python贪心算法
    Python贪心算法简介目录Python贪心算法简介贪心算法的基本步骤贪心算法的适用场景经典贪心算法问题1.**零钱兑换问题**2.**区间调度问题**3.**背包问题**贪心算法的优缺点优点：缺点：结语贪心算法（GreedyAlgorithm）是一种在每一步选择中都采取当前最优或最优解的算法。它的核心思想是，在保证每一步局部最优的情况下，希望通过贪心选择达到全局最优解。虽然贪心算法并不总能得到全
  • 非对称加密算法————RSA理论及详情 hu19930613
    转自：https://www.kancloud.cn/kancloud/rsa_algorithm/48484一、一点历史1976年以前，所有的加密方法都是同一种模式：（1）甲方选择某一种加密规则，对信息进行加密；（2）乙方使用同一种规则，对信息进行解密。由于加密和解密使用同样规则（简称"密钥"），这被称为"对称加密算法"（Symmetric-keyalgorithm）。这种加密模式有一个最大弱点
  • 数据结构 1 五花肉村长 数据结构算法开发语言c语言visualstudio
    1.什么是数据结构数据结构（DataStructure）是计算机存储和组织数据的方式，是指相互之间存在的一种或多种特定关系的数据元的集合。2.什么是算法算法（Algorithm）就是定义良好的计算过程，他取一个或一组的值为输入，并产生出一个或一组值作为输出。简单来说算法就是一系列的计算步骤，用来将输入数据转化成输出结果。3.数据结构和算法的书籍资料学习完数据结构知识，可以去看《剑指offer》和《
  • 三点or多点的变换矩阵求解opencv & eigen 合工大机器人实验室 C++矩阵opencv线性代数
    《Estimating3-DRigidBodyTransformations:AComparisonofFourMajorAlgorithms》，它使用SVD方法计算T和t。只要算出变换矩阵，就可以算出A坐标系的一个点P在坐标系B里的对应点坐标，即R为3x3的转换矩阵，t为3x1的位移变换向量，这里点坐标均为3x1的列向量（非齐次形式，齐次形式下为4x1列向量，多出的一个元素值补1而已）。理论上只
  • 详解贪心算法 凭君语未可 算法软考算法贪心算法
    贪心算法什么是贪心算法？贪心算法的特点贪心算法的应用场景贪心算法的基本思路贪心算法的经典应用1.活动选择问题2.最小硬币找零问题3.霍夫曼编码问题贪心算法的正确性贪心算法的优缺点总结什么是贪心算法？贪心算法（GreedyAlgorithm）是一种基于每一步都选择当前最优解的算法设计思想。它在每个阶段总是做出在当前看来最优的选择（局部最优解），而不回溯或考虑整个问题的全局最优性。它期望通过这样逐步构
  • 算法设计与分析 合并排序的递归实现算法 Jxcupupup 算法算法算法设计与分析
    合并排序的递归实现算法。输入：先输入进行合并排序元素的个数，然后依次随机输入（或随机生成）每个数字。输出：元素排序后的结果，数字之间不加任何标识符。示//完整代码在GitHub上//https://github.com/Jxcup/Course_Algorithm_Analysis-Design/blob/main/MergeSort_iteration.cpp//合并排序递归#includeus
  • c语言输入两个字符串 按字典数序比较大小,算法学习笔记（一）C++排序函数、映射技巧与字典树... Nature自然科研 c语言输入两个字符串按字典数序比较大小
    1.头文件algorithm中有函数sort()用于排序，参数为：排序起始地址，排序结束地址，排序规则(返回bool型)例如，要将array[]={5,7,1,2,9}升序排列，则使用：boolcmp(inta,intb);intmain(){intarray[]={5,7,1,2,9};sort(array,array+5,cmp);for(inti=0;icoutb)returnfalse;e
  • 遗传算法（Genetic Algorithm,GA）-基于MATLAB环境实现 朱佩棋（代码版） 启发式算法启发式算法算法matlab
    1.GA简介geneticalgorithm，美国Holland教授创立，基于达尔文进化论和孟德尔的遗传学说。遗传算法类比了生物界中自然选择、交叉、变异等自然进化方式，利用数码串类比染色体，通过选择、交叉、变异等遗传算子模拟生物的进化过程。1.1遗传算法的流程1.编码伪代码：2.产生初始群体Chooseinitialpopulation3.计算适应度Evaluatethefitnessofeach
  • 【译】Swift算法俱乐部-布隆过滤器 Andy_Ron
    Swift算法俱乐部本文是对SwiftAlgorithmClub翻译的一篇文章。SwiftAlgorithmClub是raywenderlich.com网站出品的用Swift实现算法和数据结构的开源项目，目前在GitHub上有18000+⭐️，我初略统计了一下，大概有一百左右个的算法和数据结构，基本上常见的都包含了，是iOSer学习算法和数据结构不错的资源。andyRon/swift-algori
  • AdaBoost算法（AdbBoost Algorithm）—有监督学习方法、非概率模型、判别模型、非线性模型、非参数化模型、批量学习 剑海风云 ArtificialIntelligence人工智能机器学习提升方法AdaBoost
    定义输入:训练数据集T={(x1,y1),(x2,y2),⋯ ,(xN,yN)}T=\{(x_1,y_1),(x_2,y_2),\cdots,(x_N,y_N)\}T={(x1,y1),(x2,y2),⋯,(xN,yN)},其中，xi∈χ⊆Rn,yi∈y={−1,+1}x_i\in\chi\subseteqR^n,y_i\in{\tty}=\{-1,+1\}xi∈χ⊆Rn,yi∈y={−1,+1}
  • Study Plan For Algorithms - Part29 五月的风与火 StudyPlanForAlgorithmspython算法数据结构
    1.在排序数组中查找数字统计一个数字在排序数组中出现的次数。方法一：defsearch(nums,target):returnhelper(nums,target)-helper(nums,target-1)defhelper(nums,target):i=0j=len(nums)-1whileitargetor(lowerandnums[mid]>=target):right=mid-1else
  • 斐波纳契数列(f(n)=f(n-1)+f(n-2))问题 剑海风云 Algorithm算法数列
    packageorg.nxt.algorithm.series;importjava.math.BigInteger;/***fibonacciseries*@authornanxiaotao**/publicclassFibonacciSeries{privatestaticBigInteger[][]matrix(BigInteger[][]arrLeft,BigInteger[][]arrR
  • Kamada-Kawai 布局算法简介，nx.kamada_kawai_layout(G) 小桥流水---人工智能 人工智能深度学习机器学习算法算法python人工智能
    nx.kamada_kawai_layout(G)是NetworkX中用于图布局的一个函数，它基于Kamada-Kawai弹簧嵌入算法（Kamada-KawaiSpringLayoutAlgorithm）。这是一个经典的力导向布局算法，它特别适用于中小型图的可视化，能够让节点的位置更直观地反映它们之间的关系。Kamada-Kawai布局算法简介Kamada-Kawai算法是一种用于图的二维或三维可
  • 旧版中 pytorch.rfft 函数与新版 pytorch.fft.rfft 函数对应修改问题 带鱼的鱼香肉丝 pytorchPythonpytorchpythonfft
    旧版中pytorch.rfft函数与新版pytorch.fft.rfft函数对应修改问题前言一、旧版pytorch.rfft()函数解释二、新版pytorch.fft.rfft()函数解释三、总结前言这两天整理谱池化操作，需要用到傅里叶变换这个函数。后来提升了pytorch的版本以后，发现之前的torch.rfft()函数在新版的pytorch中使用会报错，后来查阅资料，发现是新版的参数有些变动。
  • 翻译 Compaction wiki i_need_job
    网址：https://github.com/facebook/rocksdb/wiki/Compaction有道CompactionCompactionalgorithmsconstraintheLSMtreeshape.Theydeterminewhichsortedrunscanbemergedbyitandwhichsortedrunsneedtobeaccessedforareadoper
  • Go-Snowflake 项目教程 喻季福
    Go-Snowflake项目教程go-snowflake❄AnLockFreeIDGeneratorforGolangbasedonSnowflakeAlgorithm(Twitterannounced).项目地址:https://gitcode.com/gh_mirrors/go/go-snowflake项目介绍Go-Snowflake是一个基于Go语言实现的分布式唯一ID生成器，灵感来源于Tw
  • 2023ICPC济南站训练补题 farawaytravelerchy ACM-ICPC训练补题算法python
    title:2023ICPC济南站VP补题记录(第48届)date:2024-01-1812:16:23mathjax:truetags:XCPCcategories:Algorithm文章目录2023ICPC济南站训练补题注:暂时更新vp时ac的4道题，其余题目之后持续更新[Problem-D-LargestDigit](https://codeforces.com/gym/104901/pro
  • 【算法】浅析贪心算法 Ustinian_310 算法贪心算法python
    贪心算法：高效解决问题的策略1.引言在计算机科学和优化领域，贪心算法是一种常用的解决问题的策略。它以当前情况为基础，做出最优选择，从而希望最终结果也是最优的。本文将带你了解贪心算法的原理、使用方法及其在实际应用中的意义，并通过代码示例和图示帮助大家更好地理解。2.贪心算法简介2.1定义贪心算法（GreedyAlgorithm）是一种在每一步选择中都采取当前状态下最优（即最有利）的选择，从而希望导致
  • 自幂数判断c++ 呃m c++比赛真题c++
    题目描述样例输入3152111153样例输出FFT代码如下：#includeusingnamespacestd;longlongm,a;intmain(){cin>>m;for(inti=1;i>a;longlongt=a,n[10],cc=0,s=0;while(t!=0){//求位数与拆位n[cc]=t%10;t=t/10;cc++;}for(intj=0;j
  • OpenCV结构分析与形状描述符（8）点集凸包计算函数convexHull()的使用 jndingxin OpenCVopencv人工智能计算机视觉
    操作系统：ubuntu22.04OpenCV版本：OpenCV4.9IDE:VisualStudioCode编程语言：C++11算法描述查找一个点集的凸包。函数cv::convexHull使用斯克拉斯基算法（Sklansky’salgorithm）来查找一个二维点集的凸包，在当前实现中该算法的时间复杂度为O(NlogN)。函数cv::convexHull是OpenCV库中的一个功能，用于计算一组二
  • Java算法之判断平衡二叉树 持续输出... #Java算法算法
    判断一棵二叉树是否是平衡二叉树（即AVL树）是一个常见的问题。平衡二叉树的定义是：对于树中的每个节点，其左右子树的高度差不超过1。我们可以通过递归的方法来判断一棵二叉树是否是平衡的packagecom.huawei.od.huawei.algorithm;/***@ClassName:IsBalancedBinaryTree是否是平衡二叉树*@Desc:判断一棵二叉树是否是平衡二叉树（即AVL树）
  • Python深度学习-环境 cunzai1985 tensorflowpython深度学习人工智能anaconda
    Python深度学习-环境(PythonDeepLearning-Environment)Inthischapter,wewilllearnabouttheenvironmentsetupforPythonDeepLearning.Wehavetoinstallthefollowingsoftwareformakingdeeplearningalgorithms.在本章中，我们将学习为Python
  • 探索图形算法的奇妙世界：goraph 孔岱怀
    探索图形算法的奇妙世界：goraphgoraphPackagegoraphimplementsgraphdatastructureandalgorithms.项目地址:https://gitcode.com/gh_mirrors/go/goraph在编程领域，数据结构和算法是构建高效应用的基础。今天，我们要向您推荐一款名为【goraph】的开源项目，它是一个用Go语言实现的图形数据结构及其算法库。
  • 【小白深度教程 1.5】手把手教你用立体匹配进行双目深度估计，以及 3D 点云生成（含 Python 代码解读） 小寒学姐学AI 从零开始的深度补全和深度估计3dpython人工智能计算机视觉自动驾驶深度学习笔记
    【小白深度教程1.5】手把手教你用立体匹配进行双目深度估计，以及3D点云生成（含Python代码解读）1.立体匹配的原理2.块匹配算法（BlockMatchingAlgorithm）2.1代码中的立体匹配过程概述2.2代码原理及公式2.2.1.窗口匹配和代价函数（SAD）2.2.2.匹配过程2.2.3.视差图生成2.3代码的整体算法流程2.4性能与优化3.加载双目图像计算视差4.读取相机参数并计算
  • 关于多变量超扭曲算法的到达时间评估 beegreen 控制与信号处理算法动态规划数学建模
    关于多变量超扭曲算法的到达时间评估I.引言II.问题陈述III.李雅普诺夫函数的性质IV.到达时间估计V.原始系统的到达时间估计VI.最差干扰VII.数值问题和示例A.示例VIII.结论致谢参考文献REFERENCESOnMultivariableSuper-TwistingAlgorithmReachingTimeAssessment摘要——本文提供了一种基于线性矩阵不等式（LMI）的程序，用于
  • SSH Secure File Transfer Client连接远程设备报“algorithm negotiation failed”错的解决方法 成长Bar uinx/linuxnegotiationfailedalgorithmnegotiatio
    SSHSecureFileTransferClient连接远程设备报“algorithmnegotiationfailed”错的解决方法sshclient报algorithmnegotiationfailed的解决方法之一是修改sshd的配置文件，请参考以下三个步骤进行解决该问题。第一步：进入配置文件/etc/ssh/sshd_config第二步：在配置文件中添加Ciphersaes128-cbc
  • 机器学习系列12：反向传播算法 SuperFengCode 机器学习系列机器学习神经网络反向传播算法梯度检验机器学习笔记
    当我们要运用高级算法进行梯度下降时，需要计算两个值，代价函数和代价函数的偏导数：代价函数我们之前已经知道怎么求了，现在只需要求代价函数的偏导数即可。采用如下方法，先进行前向传播算法，然后再进行反向传播算法（BackpropagationAlgorithm），反向传播算法与前向传播算法方向相反，它用来求代价函数的偏导数。具体过程看下图：用δ作为误差，计算方法为：有时我们在运用反向传播算法时会遇到bu
  • [Algorithm][综合训练][栈和排序][加减]详细讲解 DieSnowK [OJ]#[综合训练]Algorithm算法综合训练栈和排序加减C++详细讲解
    目录1.栈和排序1.题目链接2.算法原理详解&&代码实现2.加减1.题目链接2.算法原理详解&&代码实现1.栈和排序1.题目链接栈和排序2.算法原理详解&&代码实现解法：栈+贪心->每次尽可能先让当前需要的最大值弹出去vectorsolve(vector&a){intn=a.size();vectorhash(n+1,false);vectorret;intaim=n;stackst;for(au
  • What are some of halcon‘s best algorithms that opencv doesn‘t implement 0010000100 OpenCVopencv人工智能
    HALCON,ahighlyoptimizedmachinevisionlibrary,offersarangeofadvancedalgorithmsthatOpenCVeitherdoesn’timplementorhandlesdifferently.SomeofthekeystrengthsofHALCONcomparedtoOpenCVinclude:Shape-BasedMatchin
  • [ A*实现 ] C++，矩阵地图 Arik (IoT) 移动机器人路径规划路径规划
    参考文献：A*寻路算法C++简单实现（csdn.net）ROSpackageofAstaralgorithm(github.com)实现代码：https://gitee.com/upcgyl/astar.git存在问题：地图目前必须是可搜索到路径周围点寻找太过复杂OpenList和CloseList结构不统一导致查找函数需要写两个后续优化：思考二叉堆的实现方式优化地图输入区分linux端：增加Op
  • TOMCAT在POST方法提交参数丢失问题 357029540 javatomcatjsp
    摘自http://my.oschina.net/luckyi/blog/213209 昨天在解决一个BUG时发现一个奇怪的问题，一个AJAX提交数据在之前都是木有问题的，突然提交出错影响其他处理流程。 检查时发现页面处理数据较多，起初以为是提交顺序不正确修改后发现不是由此问题引起。于是删除掉一部分数据进行提交，较少数据能够提交成功。 恢复较多数据后跟踪提交FORM DATA ，发现数
  • 在MyEclipse中增加JSP模板 删除-2008-08-18 ljy325 jspxmlMyEclipse
    在D:\Program Files\MyEclipse 6.0\myeclipse\eclipse\plugins\com.genuitec.eclipse.wizards_6.0.1.zmyeclipse601200710\templates\jsp  目录下找到Jsp.vtl，复制一份，重命名为jsp2.vtl,然后把里面的内容修改为自己想要的格式，保存。 然后在 D:\Progr
  • JavaScript常用验证脚本总结 eksliang JavaScriptjavaScript表单验证
         转载请出自出处：http://eksliang.iteye.com/blog/2098985        下面这些验证脚本，是我在这几年开发中的总结，今天把他放出来，也算是一种分享吧，现在在我的项目中也在用！包括日期验证、比较，非空验证、身份证验证、数值验证、Email验证、电话验证等等...! &nb
  • 微软BI（4） 18289753290 微软BI SSIS
    1） Q:查看ssis里面某个控件输出的结果：  A MessageBox.Show(Dts.Variables["v_lastTimestamp"].Value.ToString()); 这是我们在包里面定义的变量 2):在关联目的端表的时候如果是一对多的关系，一定要选择唯一的那个键作为关联字段。 3) Q：ssis里面如果将多个数据源的数据插入目的端一
  • 定时对大数据量的表进行分表对数据备份 酷的飞上天空 大数据量
    工作中遇到数据库中一个表的数据量比较大，属于日志表。正常情况下是不会有查询操作的，但如果不进行分表数据太多，执行一条简单sql语句要等好几分钟。。   分表工具：linux的shell + mysql自身提供的管理命令 原理：使用一个和原表数据结构一样的表，替换原表。   linux shell内容如下： =======================开始 
  • 本质的描述与因材施教 永夜-极光 感想随笔
             不管碰到什么事,我都下意识的想去探索本质,找寻一个最形象的描述方式。        我坚信,世界上对一件事物的描述和解释,肯定有一种最形象,最贴近本质,最容易让人理解        &
  • 很迷茫。。。 随便小屋 随笔
    小弟我今年研一，也是从事的咱们现在最流行的专业（计算机）。本科三流学校，为了能有个更好的跳板，进入了考研大军，非常有幸能进入研究生的行业（具体学校就不说了，怕把学校的名誉给损了）。   先说一下自身的条件，本科专业软件工程。主要学习就是软件开发，几乎和计算机没有什么区别。因为学校本身三流，也就是让老师带着学生学点东西，然后让学生毕业就行了。对专业性的东西了解的非常浅。就那学的语言来说
  • 23种设计模式的意图和适用范围 aijuans 设计模式
    Factory Method 意图 定义一个用于创建对象的接口，让子类决定实例化哪一个类。Factory Method 使一个类的实例化延迟到其子类。 　　适用性 当一个类不知道它所必须创建的对象的类的时候。 　　当一个类希望由它的子类来指定它所创建的对象的时候。 　　当类将创建对象的职责委托给多个帮助子类中的某一个，并且你希望将哪一个帮助子类是代理者这一信息局部化的时候。 Abstr
  • Java中的synchronized和volatile aoyouzi javavolatilesynchronized
    说到Java的线程同步问题肯定要说到两个关键字synchronized和volatile。说到这两个关键字，又要说道JVM的内存模型。JVM里内存分为main memory和working memory。 Main memory是所有线程共享的，working memory则是线程的工作内存，它保存有部分main memory变量的拷贝，对这些变量的更新直接发生在working memo
  • js数组的操作和this关键字 百合不是茶 js数组操作this关键字
    js数组的操作;   一:数组的创建: 1、数组的创建 var array = new Array();　//创建一个数组 var array = new Array([size]);　//创建一个数组并指定长度，注意不是上限，是长度 var arrayObj = new Array([element0[, element1[, ...[, elementN]]]
  • 别人的阿里面试感悟 bijian1013 面试分享工作感悟阿里面试
    原文如下：http://greemranqq.iteye.com/blog/2007170         一直做企业系统，虽然也自己一直学习技术，但是感觉还是有所欠缺，准备花几个月的时间，把互联网的东西，以及一些基础更加的深入透析，结果这次比较意外，有点突然，下面分享一下感受吧！    &nb
  • 淘宝的测试框架Itest Bill_chen springmaven框架单元测试JUnit
    Itest测试框架是TaoBao测试部门开发的一套单元测试框架，以Junit4为核心， 集合DbUnit、Unitils等主流测试框架，应该算是比较好用的了。 近期项目中用了下，有关itest的具体使用如下： 1.在Maven中引入itest框架： <dependency>   <groupId>com.taobao.test</groupId&g
  • 【Java多线程二】多路条件解决生产者消费者问题 bit1129 java多线程
    package com.tom; import java.util.LinkedList; import java.util.Queue; import java.util.concurrent.ThreadLocalRandom; import java.util.concurrent.locks.Condition; import java.util.concurrent.loc
  • 汉字转拼音pinyin4j 白糖_ pinyin4j
    以前在项目中遇到汉字转拼音的情况，于是在网上找到了pinyin4j这个工具包，非常有用，别的不说了，直接下代码：   import java.util.HashSet; import java.util.Set; import net.sourceforge.pinyin4j.PinyinHelper; import net.sourceforge.pinyin
  • org.hibernate.TransactionException: JDBC begin failed解决方案 bozch ssh数据库异常DBCP
    org.hibernate.TransactionException: JDBC begin failed:     at org.hibernate.transaction.JDBCTransaction.begin(JDBCTransaction.java:68)    at org.hibernate.impl.SessionImp
  • java-并查集（Disjoint-set）-将多个集合合并成没有交集的集合 bylijinnan java
    import java.util.ArrayList; import java.util.Arrays; import java.util.HashMap; import java.util.HashSet; import java.util.Iterator; import java.util.List; import java.util.Map; import java.ut
  • Java PrintWriter打印乱码 chenbowen00 java
    一个小程序读写文件，发现PrintWriter输出后文件存在乱码，解决办法主要统一输入输出流编码格式。 读文件： BufferedReader 从字符输入流中读取文本，缓冲各个字符，从而提供字符、数组和行的高效读取。 可以指定缓冲区的大小，或者可使用默认的大小。大多数情况下，默认值就足够大了。 通常，Reader 所作的每个读取请求都会导致对基础字符或字节流进行相应的读取请求。因
  • [天气与气候]极端气候环境 comsci 环境
          如果空间环境出现异变...外星文明并未出现,而只是用某种气象武器对地球的气候系统进行攻击,并挑唆地球国家间的战争,经过一段时间的准备...最大限度的削弱地球文明的整体力量,然后再进行入侵......      那么地球上的国家应该做什么样的防备工作呢?  &n
  • oracle order by与union一起使用的用法 daizj UNIONoracleorder by
    当使用union操作时，排序语句必须放在最后面才正确，如下： 只能在union的最后一个子查询中使用order by，而这个order by是针对整个unioning后的结果集的。So： 如果unoin的几个子查询列名不同，如 Sql代码  select supplier_id, supplier_name  from suppliers  UNI
  • zeus持久层读写分离单元测试 deng520159 单元测试
    本文是zeus读写分离单元测试,距离分库分表,只有一步了.上代码: 1.ZeusMasterSlaveTest.java package com.dengliang.zeus.webdemo.test; import java.util.ArrayList; import java.util.List; import org.junit.Assert; import org.j
  • Yii 截取字符串(UTF-8) 使用组件 dcj3sjt126com yii
    1.将Helper.php放进protected\components文件夹下。 2.调用方法：   Helper::truncate_utf8_string($content,20,false);   //不显示省略号  Helper::truncate_utf8_string($content,20);  //显示省略号  &n
  • 安装memcache及php扩展 dcj3sjt126com PHP
    安装memcache    tar zxvf memcache-2.2.5.tgz     cd memcache-2.2.5/     /usr/local/php/bin/phpize (?)    ./configure --with-php-confi
  • JsonObject 处理日期 feifeilinlin521 javajsonJsonOjbectJsonArrayJSONException
        写这边文章的初衷就是遇到了json在转换日期格式出现了异常 net.sf.json.JSONException: java.lang.reflect.InvocationTargetException  原因是当你用Map接收数据库返回了java.sql.Date 日期的数据进行json转换出的问题话不多说  直接上代码  &n
  • Ehcache（06）——监听器 234390216 监听器listenerehcache
    监听器          Ehcache中监听器有两种，监听CacheManager的CacheManagerEventListener和监听Cache的CacheEventListener。在Ehcache中，Listener是通过对应的监听器工厂来生产和发生作用的。下面我们将来介绍一下这两种类型的监听器。  
  • activiti 自带设计器中chrome 34版本不能打开bug的解决 jackyrong Activiti
      在acitivti modeler中，如果是chrome 34，则不能打开该设计器，其他浏览器可以， 经证实为bug，参考 http://forums.activiti.org/content/activiti-modeler-doesnt-work-chrome-v34 修改为，找到 oryx.debug.js 在最头部增加 if (!Document.
  • 微信收货地址共享接口-终极解决 laotu5i0 微信开发
       最近要接入微信的收货地址共享接口，总是不成功，折腾了好几天，实在没办法网上搜到的帖子也是骂声一片。我把我碰到并解决问题的过程分享出来，希望能给微信的接口文档起到一个辅助作用，让后面进来的开发者能快速的接入，而不需要像我们一样苦逼的浪费好几天，甚至一周的青春。各种羞辱、谩骂的话就不说了，本人还算文明。    如果你能搜到本贴，说明你已经碰到了各种 ed
  • 关于人才 netkiller.github.com 工作面试招聘netkiller人才
    关于人才 每个月我都会接到许多猎头的电话，有些猎头比较专业，但绝大多数在我看来与猎头二字还是有很大差距的。 与猎头接触多了，自然也了解了他们的工作，包括操作手法，总体上国内的猎头行业还处在初级阶段。 总结就是“盲目推荐，以量取胜”。 目前现状 许多从事人力资源工作的人，根本不懂得怎么找人才。处在人才找不到企业，企业找不到人才的尴尬处境。 企业招聘，通常是需要用人的部门提出招聘条件，由人
  • 搭建 CentOS 6 服务器 - 目录 rensanning centos
    (1) 安装CentOS ISO（desktop/minimal）、Cloud（AWS/阿里云）、Virtualization（VMWare、VirtualBox） 详细内容 (2) Linux常用命令 cd、ls、rm、chmod...... 详细内容 (3) 初始环境设置 用户管理、网络设置、安全设置...... 详细内容 (4) 常驻服务Daemon
  • 【求助】mongoDB无法更新主键 toknowme mongodb
      Query query = new Query();          query.addCriteria(new Criteria("_id").is(o.getId()));                &n
  • jquery 页面滚动到底部自动加载插件集合 xp9802 jquery
    很多社交网站都使用无限滚动的翻页技术来提高用户体验，当你页面滑到列表底部时候无需点击就自动加载更多的内容。下面为你推荐 10 个 jQuery 的无限滚动的插件： 1. jQuery ScrollPagination jQuery ScrollPagination plugin 是一个 jQuery 实现的支持无限滚动加载数据的插件。 2. jQuery Screw S
按字母分类： ABCDEFGHIJKLMNOPQRSTUVWXYZ其他