深度学习新的采样方式和损失函数--论文笔记
深度学习新的采样方式和损失函数--论文笔记
论文《Sampling matters in deep embedding learning》
论文地址:https://arxiv.org/pdf/1706.07567.pdf
该论文为2017年6月上传至arxiv。主要研究的是深度嵌入学习(deep embedding learning)中的采样问题和损失函数的问题。作者分析了contrastive loss和triplet loss,提出了一种新的采样方式(distance weighted sampling)和一种新的loss function(margin based loss)。证明了训练模型时,数据的采样方式和loss function的形式对结果有着同样重要的影响。实验证明,该工作提出的方法在多个数据集上都能够得到最好的效果。
在机器学习领域,对loss function的研究已经有很多了,loss function的好坏,直接影响到模型的训练结果。作者在本文中只讨论深度嵌入学习,可以简单理解为基于深度模型的学习,之所以叫嵌入学习(embedding learning)是因为该类模型的核心思想是:建立一个嵌入空间,在该空间中,相似的样本距离近,不相似的样本距离远。
传统loss function
设f(xi)为嵌入空间中的数据点,我们的目标是使得嵌入空间中相似的点距离近,不相似的点距离远。设两样本的欧氏距离为:
对于正样本对,有yij=1,对于负样本对,则有yij=0。
Contrastive loss
其目标函数如下:
该loss的问题在于,它需要定义一个固定的a,这其实就默认了所有每类样本的分布都相同,这其实是一个很强的假设。
Triplet loss
其目标函数如下:
它使得正负例样本之间的距离尽可能接近于a,这就不管数据的分布了。它能够补足contrastive loss的缺点,使得嵌入空间可以任意扭曲。作者总结称,triplet loss超越constrative loss的原因有两个:1)constrative loss有一个固定的a,而triplet loss能够灵活适应各种空间形状,一定程度上能够抵御噪声的影响;2)triplet loss只要求正例与正例的距离小于正例与负例的距离即可,而constrative loss则还要尽量使所有的正例集中在一起,而这点是不必要的。
对于contrastive loss来说,使用hard negative mining的方法,能够使得模型收敛得更快;然而,如果使用的是triplet loss,hard negative mining很可能会模型坍塌。这里所说的hard negative mining是指:对于某些任务,比如人脸检测,直接进行采样,训练出的模型效果不会太好,因为模型可能会检测出很多假正例;因此,可以取置信度很高的为正例的真负例,与正例一起训练,这些负例就被称为hard negative mining。对于模型坍塌的问题,可以这样解释,设一个anchor样本a,负例样本n,如果对负例样本f(xn)求梯度,可得:
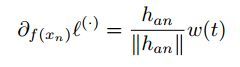
其中
Hard negative样本通常离anchor的距离较小,即han较小,这时如果有噪声,那么这种采样方式就很容易受到噪声的影响,从而造成训练时的模型坍塌。
由于模型坍塌的问题,FaceNet[1]提出了一种semi-hard negative mining的方法:给定一个anchor样本a,一个正例样本p,对于负例的采样,使用以下公式:

这样采样出来的负例,不至于过于hard。
Distance Weighted sampling
在现实状态下,如果同类样本是均匀分布在其各自的簇中的,如果我们对所有的样本进行两两采样,计算其距离,最终得到的点对距离分布(distribution of pairwise distances)有着如下关系:

而且,最佳的采样状态是对于分散均匀的负样本,进行均匀地采样。具体证明,可以参考论文[2]。因此,作者提出了一种新的采样方法Distance weighted sampling。给定一个anchor样本a,负例样本的选择方法如下:
如图1所示,为各种采样方法在一个模拟数据集上的结果,纵轴为数据梯度的方差。从图中可以看出,hard negative mining方法采样的样本都处于高方差的区域,如果数据集中有噪声的话,采样很容易受到噪声的影响,从而导致模型坍塌。随机采样的样本容易集中在低方差的区域,从而使得loss很小,但此时模型实际上并没有训练好。Semi-hard negative mining采样的范围很小,这很可能导致模型在很早的时候就收敛,loss下降很慢,但实际上此时模型也还没训练好;而本文提出的方法,能够实现在整个数据集上均匀采样。
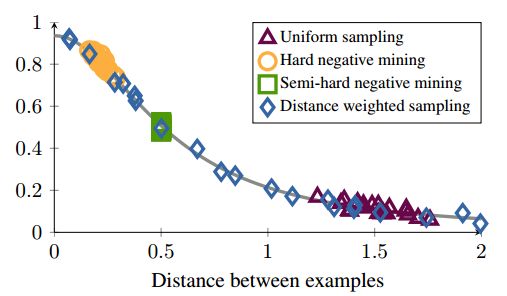
图1 各种采样结果在模拟数据集上的采样结果
Margin based loss
如图2所示,为不同loss function取不同样本时损失的曲线图。可以根据constractive loss和triplet loss的公式,来理解2a和2b。这里主要观察2b,如果采样的时候采的都是hard negative 样本,即Dan的值很小,从图中可以看出,负例的梯度会非常小(也可以对目标函数进行求导,得出相同的结论),此时就会导致模型坍塌。一个简单的改进方法就是,将triplet loss中的二次项换成一次项,这时目标函数的导数固定为1,能够解决梯度消失的问题,这里其实可以类比深度学习中应用广泛的RELU激活函数。

图2 loss vs pairwise distance
作者提出了一个新的目标函数Margin based loss,这个函数设计的目标是:1)能像triplet loss一样灵活;2)能够自适应不同的数据分布;3)能够像contrastive loss一样计算高效。
首先,定义一个自适应的margin:
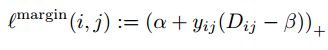
我们称anchor样本与正例样本之间的距离为正例对距离;称anchor样本与负例样本之间的距离为负例对距离。公式中的参数beta定义了正例对距离与负例对距离之间的界限,如果正例对距离Dij大于beta,则损失加大;或者负例对距离Dij小于beta,损失加大。A控制样本的分离间隔;当样本为正例对时,yij为1,样本为负例对时,yij为-1。如图2d所示,为该目标函数的损失曲线图,与2a比较,它放松了对正例的约束。将其与2c比较,在有损失的地方,它们的导数都是1,具有良好的性质,且2d的形状不受限于数据集本身,而只与a和beta有关。
为了实现像triplet loss一样的灵活性,可以将beta设置为与样本有关的值:
其中, beta(class)称为样本偏置, beta(img)称为类别偏置。这里需要注意,第一个beta(0)是人工定义的初始值,利用梯度下降,不断调整beta(class)和beta(img)的值(就如同调整神经网络的参数)以在训练集上达到最优,这时能够得到最优的beta(class)和beta(img)(每个类一个beta(class),每个样本一个beta(img))。在调整beta的值的时候,可以对其整体求导
用来指导beta值的调整。从公式可以看出,beta的值似乎越大越好,其值越大,负例离anchor点的距离也就越大,不容易受到噪声的影响(上文已经提到了具体细节)。为了对beta进行规划化,需要给它一个限制,作者引入了一个超参数v,并定义:

这个v参数能够调整margin两边,违反margin数据点的数量,具体原理可见[3]中的v-trick。
实验结果
数据集:Stanford Online Products, CARS196, CUB200-2011, CASIA-WebFace, LFW.
实验:图片检索和图片聚类(Stanford Online Products, CARS196, CUB200-2011),人脸验证(CASIA-WebFace, LFW)。
模型:ResNet-50[4]
初始化参数:beta(0)=1.2,beta(class)=0,beta(img)=0.
首先,在Stanford Online Products数据集上进行实验,来测试不同loss function和采样方式对结果的影响,ResNet-50模型从头开始训练。结果如表1所示,在semi-hard采样方法中,constrastive loss和triplet loss的性能类似,而如果使用随机采样,constrastive loss的性能要差很多(triplet loss不能随机采样),这其实反证了一个结论:triplet loss的性能不仅仅来自于其自身的函数结构,也与采样方式有很大的关系。
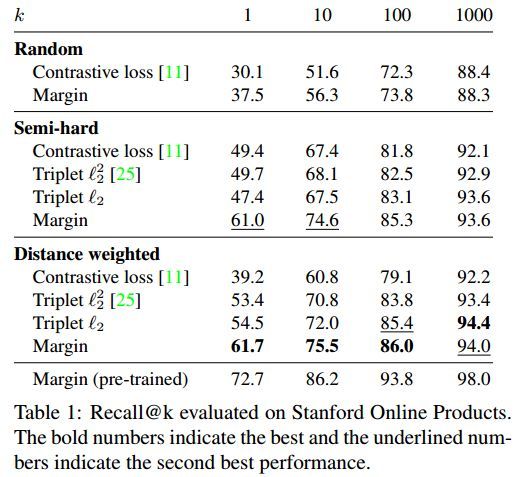
Distance weighted采样方法对于除了constrastive loss之外的所有loss function都有加强的效果。作者称该采样方法在constrastive loss上结果差的原因是它对于超参数特别敏感,无法找到一个合适的参数。
作者也实验了pre-trained的模型效果,提升了大概10%的效果。
由于pre-trained模型效果更好,因此接下来的时候均使用该模型。如图3所示,为图片搜索的结果,可以看到本文基于margin的方法要优于triplet loss方法。

图3 图片搜索结果
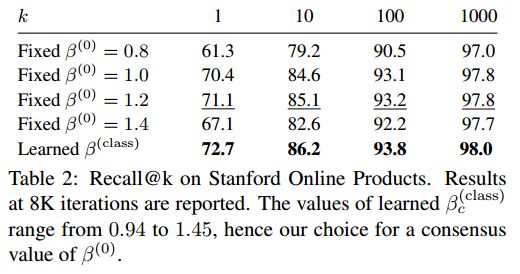
作者还对比了固定的beta和本文灵活的beta对结果的影响。由表2的结果可知,灵活的beta对于结果的确是有提升的。注意,这里作者只说了beta(class),得到了更好的效果,他也试验了beta(img),但结果很不稳定,很有可能是过拟合的原因。因此,在实验的时候,可以只考虑beta(class),去除beta(img)。
如图4所示,作者对loss function的稳定性进行了实验,将batch中图片的数量分为改为2和10,有结果可知,本文基于margin的方法要比triplet loss方法稳定很多。

图4 Margin loss和triplet loss稳定性对比
如图5所示,是对收敛速度的实验,其中本文算法收敛最快且效果最好,triplet loss其次,contrastive loss就要差很多了。

图5 不同loss的收敛速度对比
本文还与目前最好的图片搜索和聚类方法进行了比较,结果如表3、4、5所示,可以看到本文算法效果最好。


表6是人脸验证的结果,本文算法accuracy结果依然最好。

总结
本文主要对contrastive loss、triplet loss目标函数和各种采样策略进行了分析,结合分析结果,提出了一种新的采样方式distance weighted sampling和一种新的损失函数margin-based loss。这两种方法能够显著提高模型各方面的性能,取得了在多个数据集上至今最好的结果。有一点吐槽一下,文章的题目只提到“sampling matters”,但实际上文章的算法共两个部分:采样和损失函数。这样取名字仅仅是因为目前该领域损失函数的工作太多,采样的工作太少么?
参考文献
[1]Facenet: A unified embedding for face recognition and clustering.(CVPR2015)
[2]The sphere game in n dimensions. http://faculty.madisoncollege.edu/alehnen/sphere/hypers.htm. Accessed: 2017-02-22.
[3]New support vector algorithms. Neural computation, 2000.
[4]Deep residual learning for image recognition.(CVPR 2016)