优化算法
第一课:小批量梯度下降
本周学习加快神经网络训练速度的优化算法。
我们之前学习过矢量化可以让你有效的计算所有m个样例,而不需要用一个具体的for循环就能处理整个训练集,这就是为什么我们要将所有的训练样例集中到这些巨型矩阵X中。
X为nxm维矩阵,Y为1m维矩阵。
矢量化运算能够相对更快地处理M个样例,但是如果M很大,速度也会相对变慢。
对你的整个训练集进行梯度下降,你必须先处理你的训练集,从而加快你的训练速度。即让梯度下降在处理完整个巨型的5百万训练集之前,就可使有所成效。
首先,将你的训练集拆分成更小的微小训练集,即小批量训练集,即取x1到x1000作为第一个微训练集,称为X{1}。
Y也作相应的拆分处理。第T个小批量样例,包含XT和YT,即相应1000个训练样例的输入输出对。
在这里我们引入{t}代表不同的小批量样例。
该算法每次只处理一个小批量样例X{t}、Y{t},而不是一次处理完整个训练集X Y。
小批量梯度下降是怎么实现的呢?
用矢量化的方法同时处理1000个样例。
首先对输入值运用前向传播...我们要做的和之前的梯度下降法相同,只不过之前是训练X Y,现在是训练X{t} Y{t}。
接下来运用反向传播,来计算J{t}的梯度...。
这是小批量梯度下降算法处理训练集一轮的过程。即训练集的一次遍历。 只不过在批量下降梯度法中,对训练集的一轮处理只能得到一步梯度逼近。而小批量梯度下降法中对训练集的一轮处理,可以得到5000步梯度逼近。当然你会想对训练集进行多轮遍历,你可以用另一个for循环或者while循环实现,所以你不断的训练训练集,并希望它收敛在某个近似收敛值。
小批量梯度下降法比梯度下降法要快得多,这几乎是每一个使用深度学习的人在处理一个大型数据集时会采用的算法。
那么小批量梯度算法在做什么?它为什么会奏效?
第二课:了解小批量梯度下降
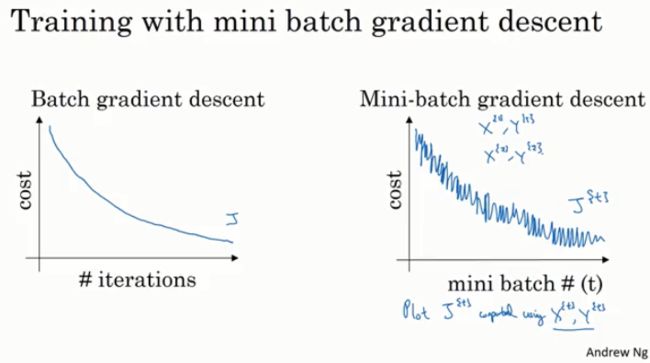
在批量梯度下降法中,每一次迭代你将遍历整个训练集,并希望代价函数的值不端缩小,如果我们用J表示代价函数,那么它应该随着迭代单调递减,如果某一次迭代它的值增加了,表示哪里肯定出了问题,也许是你的学习率过大。
而在小批量梯度下降中,画图会发现并不是每一次迭代代价函数值都会缩小,因为每一次迭代你都使用不同的训练集,所以它的趋势是下降的,但是可能有许多噪声,如果使用小批量梯度下降,经过几轮训练过,趋势应该如下图。噪声的产生可能和计算代价函数使用的那个批次的X{t} Y{t}有关,让你的代价函数值或大或小。也可能这个批次中含有一些标签错误的数据,导致代价函数有一点高等。
你必须定义的一个参数是mini-batch的大小,如果m是训练集的大小,一个极端情况是:mini-batch的大小等于m,那么这就是批量梯度下降。另一极端情况是把mini-batch的大小设置为1,就会得到一种叫随机梯度下降的算法,这里的每一条数据就是一个mini-batch。那么这两种方法在优化代价函数时图示如下:
批量梯度下降法的噪声比较小,而随机梯度下降法的噪声会比较大。而且最后随机梯度下降法不会收敛到一个点,它一般会在最低点附近摆动,但是不会到达并停在那里。实际上的mini-batch的大小在这两个极端情况之间。
原因是:
如果你使用批量梯度下降,那么你每一次迭代都会使用全部训练集,如果你的训练集非常大,那么在每一次迭代上都会花费很长的时间,相反如果你使用随机梯度下降法,使用一个样本来更新梯度,这没有问题,也可以选择较小的学习率来减少噪声,但是随机梯度下降法的一个比较大的缺点是:你失去了一个可以利用向量来加快算法速度的机会。因为你每次只处理一个样本,这是非常没有效率的。
所以更好的做法是选择一个中间值。这么做的好处是:
1.你可以使用向量的方式运算
2.你不用等待整个训练集都遍历一遍才运行梯度下降
虽然它不能保证总是达到最小值,但是相比随机梯度下降,它的噪声会比较小,而且它不会总是在最小值附近摆动。如果你有什么问题,你可以减小你的学习率。
怎么选择?
原则是:
1.如果你的训练集比较小,就是用批量梯度下降法(m<= 2000)
2.如果你有一个比较大的训练集,那么mini-batch的大小一般选择在64-512,这是因为计算机内存的布局和访问方式,因此把miini-batch的大小设置为2的幂次方代码会运行更快。
3.最后一个提醒是确保你的mini-batch,即你所有的X{t} Y{t}是可以放进你的CPU/GPU内存。当然这和你的配置以及一个训练样本的大小都有关系。即如果你把你的mini-batch的大小设置超过了GPU/CPU的内存容量,不管你怎么做,你都会发现结果比较糟糕。
mini-batch的大小也是一个超参数,可能需要你快速的搜索去确定使用哪一个值可以让代价函数J下降的更快。所以我的做法是:
尝试几个不同的值,然后看是否能找到那个能让你的梯度下降算法尽可能效率高的值。
有没有更高效的算法呢?
第三课:指数加权平均值
有几个优化算法运算速度是比梯度下降法更快的:
为了用到这些算法,你需要用到一种叫做指数加权平均的操作,在统计学中也叫做指数加权滑动平均。
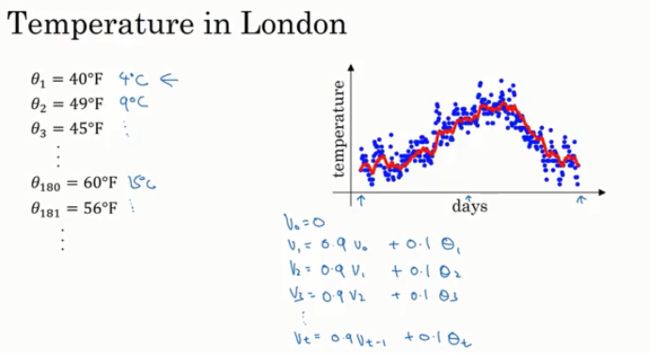
你想要计算数据的趋势即温度的局部平均或滑动平均:
首先用v0 = 0,之后每一天我们先用0.9乘以之前的值,加上0.1乘以当天的温度,之后都使用相同的加权平均。如果你这么做,你就会得到一个滑动平均图,称为每日温度的指数加权平均。
当你计算这个通式的时候,你会可以认为Vt近似于1/(1-β)天温度的平均。即当β = 0.9时,你可以认为当天温度是前十天温度的平均。
有几个点需要注意:
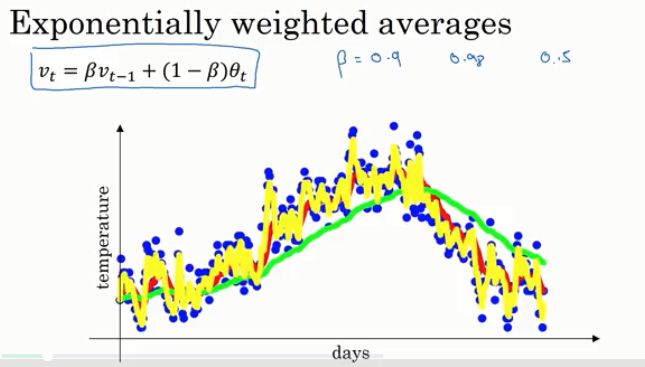
当β的值很大的时候,你得到的曲线会更平滑,因为你对更多天数的温度做了平均处理,因此曲线就波动更小,更加平滑,但另一方面,这个曲线会右移,因为你在一个更大的窗口内计算平均温度。在更大的窗口内进行平均温度的计算,这个指数加权平均的公式在温度变化时,适应的更加缓慢,这就造成了一些延迟。
当β值很小的时候,例如0.5,即在比较小的窗口内计算平均,得到的结果中会有更多的噪声,更容易收到异常值的影响,但它可以更快的适应温度变化。
通过调整这个参数,也就是我们之后会在学习算法中看到的一个超参数,就可以得到略微不同的收敛,通常取中间的这个数值效果会最好,即红线。
第四课:了解指数加权平均值
指数加权平均将是几个训练神经网络的优化算法中关键组成部分,那么这一算法的具体作用是什么?
它是如何计算每日温度的?
即将每日气温值乘以指数衰减函数然后求和,事实证明,使用链式法则,所有的系数之和等于1或者接近1,这就会涉及到下一讲中的偏差修正。
当β = 0.9时,与1/e进行比较作为足够小的判断依据,大约需要10天,即指数加权值只关注最近十天的气温值,因为十天后,气温值将降至不到目前气温值的三分之一。
当β = 0.98时,那么计算0.98的几次方可以使这个值足够小,计算出的数值为50,可以把这天的气温作为50天的平均气温。
我们就是通过这种方式获得1/(1-β)或相应天数的平均值。它能告诉你大概多少天的气温值可以作为气温均值,但这只是一种经验之谈并非正式的数学表达式。
如何在实际情况中使用它?
这个指数加权平均公式的优点之一:
不需要太多的存储空间,只需在计算机内存中保留一行数字,基于新数值,你用公式不端重写运算即可,因为高效,所以它只占用一行代码,一个单一初始值的存储和内存空间,来计算指数加权平均值,虽然这并不是计算均值的最好方法,或者是最准确的方法。如果你只需要一个移动窗口,例如,直接计算出近十天或者五十天的气温总和,除以10或者50可以给你一个更好的估计值,但是保存所有的气温值需要更多的内存。
所以当你需要计算很多变量的平均值,不论是计算还是存储效率,这个滑动平均加权算法都十分高效,这也是为什么它在机器学习中被广泛应用的原因。
什么是偏差修正?
第五课:指数加权平均值的偏差修正
它可以帮助你更精确的计算平均值。
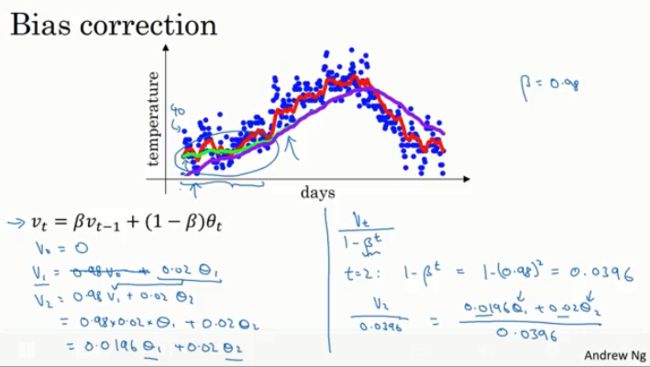
起始点很低或者说整体很低,因为设置v0 = 0。
因此在运算初期:用vt/1- β代替vt。当t很小时,消除了偏差,当t值变大,βt值将趋向于0,偏差修正值对运算基本没有影响。
即在学习初始阶段,当你还在熟悉估计值,偏差修正值可以帮你更好的估计气温值,当学习后续阶段,偏差估计对公式计算的影响会越来越小。
在机器学习中,多数的指数加权平均运算并不会使用偏差修正,因为大多数人更愿意在初始阶段用一个捎带偏差的值进行计算,不过如果在初始阶段就开始考虑偏差,即在预热阶段,偏差修正就可以帮助你尽早做出更好的估计。
接下来让我们建立一些优化算法!
第六课:具有动量的梯度下降
动量梯度下降法,几乎比标准的梯度下降法运算更快。算法的主要思想是计算梯度的指数加权平均,然后使用这个梯度来更新权重。
上下震荡会减慢梯度下降的速度,也会让你无法使用较大的学习率(会发生超调)。
即在纵轴上,你希望学习慢一点,因为不想有震荡存在,但是在横轴上没,你希望加快学习速度。
实现动量梯度下降的步骤:
在第t次迭代中,需要计算导数dw db。然后需要计算Vdw,类似于之前的Vθ。即计算W导数的滑动平均值。
然后计算Vdb。
然后使用Vdw、Vdb更新权重。
这样做可以让梯度下降的每一步变得平滑,在数次迭代之后,你会发现动量梯度下降算法的每一步在垂直方向上的震荡非常小,且在水平方向上运动更快,这会让你的算法选择更加直接的路径。
物理理解:
如果你想最小化一个碗状函数,你可以把导数项dw和db看做是一个球滚下坡时的加速度,把Vdw和Vdb看作是球的速度,导数项给了球一个加速度,然后球就会往下滚,所以它滚得越来越快,而β是一个小于1的数,所以可以把它看成是摩擦力,让球不至于无限加速下去,与梯度下降中每一步都独立于之前的步骤所不同的是:现在你的球可以向下滚动并获得动量。
具体如何实现它:
两个超参数,一个是学习率α,一个是β,参数β控制指数加权平均,常用区取值是0.9,你也可以尝试选择更合适的值,其次,是否需要进行偏差修正也是你需要考虑的事,人们通常不进行偏差修正是因为在迭代了10次以后,你的滑动平均值已经就绪,不再是一个偏差估计,所以实际上,在实现梯度下降或者是动量梯度下降时,我没有见别人使用偏差修正。初始化Vdw/Vdb = 0,但是需要和W和b有相同的维度。
最后,当你在阅读关于动量梯度下降相关的文献时,(1-β)这一项也常常被忽略,这样的情况下,α也要根据(1-β)进行调整,即重新调整学习率(所以我个人认为不要省略(1-β)这一项)。
加速你学习算法的其他方法?
第七课:RMSprop
均方根传递算法也可以加速梯度下降。
减慢b方向上的学习,同时加速至少不减慢w水平方向的学习。使用这种方法时可以发现:垂直方向上的导数要比水平方向上的更大,即在b方向上斜率很大,即db很大,而dw相对较小。
结果是在垂直方向的更新量会除以一个比较大的数,这有助于减弱震荡,而水平方向上的更新量会除以一个较小的数。使用RMSprop的效果就是对你的更新进行优化。另一个收效是你可以使用更大的学习率α,学习地更快,而不用担心在垂直方向上的发散。
实践中,dw和db可能是一个非常高维度的参数向量,直观理解是在出现震荡的维度里,你会计算得到一个更大的和值,即导数平方的加权平均,最后抑制了这些出现震荡的方向。
均方根传递:因为你对导数求了平方,而且最后取了平方根。
为了避免在动量和RMSprop中使用相同名称的超参数,这里我们使用的是β2,同时为了确保你的算法不会除以0,如果sdw的平方根非常接近0,分母就会变得很大,为了确保数值的稳定性,当你实现这个算法时,你要给分母加上一个非常非常小的ε,ε的值取多少并不重要,10-8次方是一个合理的默认值,但这智能轻微提高数值稳定性无论由于数值上的舍入或者其他的原因,你都不会除以一个过小的数0。
RMSprop和动量一样都可以降低梯度下降和小批量梯度下降中的震荡,并且让你可以选择更大的学习率α从而提高你的算法运算速度。
把RMSprop和动量结合起来?
第八课:Adam优化算法
关于RMSprop和Adam优化算法属于极少数真正有效的算法,适用于很多不同的深度学习网络结构。
Adam优化算法的本质是把RMSprop和动量算法结合起来。
首先你要进行初始化,接着在第t次迭代过程中,你需要用到一些微积分的知识用当前的mini-batch来计算dw和db。然后计算动量指数加权移动平均值。然后用同样地方式更新RMSprop中的参数。
一般在构建Adam算法的过程中,需要进行偏差修正,对vdw和vdb以及sdw和sdb进行同样的修正。
这里就是将Vdw除以偏差修正sdw的平方根加上ε!然后以此类推更新参数b!
这就是Adam算法,结合了动量和RMSprop梯度下降的优势,被广泛使用,且已经被证明在很多不同种类的神经网络架构中都是十分有效的。
这个算法中有几个超参数:
α依然很重要且需要调整,可以尝试不同的值来比较结果。业内通常对β1,β2和ε直接使用默认值,然后尝试使用不同的学习率α来看看哪个效果最好。
Adam代表自适应矩阵估计,β1代表dw的平均值,被称为第一阶的矩;β1被用于计算平方数的指数平均加权,也被称为第二矩阵。
怎么调整超参数?到底如何进行神经网络优化?学习率的衰减?
第九课:学习率衰减
有一种方法或许能使学习算法运行更快,那就是渐渐减小学习率,我们称之为学习率衰减。
当你使用小批次梯度下降,最终它会逐步向最小值靠近,但是不会完全收敛,因为你的学习率取了固定值,且不同批次也可能产生噪声。但如果你慢慢降低你的学习率,随着学习率的降低,步长会变得越来越小,所以最终将围绕着离极小值点更近的区域摆动,即使训练下去也不会漂游远离。
逐步降低学习率背后的思考是:
在学习的初始步骤中,你可以采取大得多的步长,但随着学习收敛于一点时,较低的学习率可以允许你采取更小的步长,那怎么实现学习率的衰减呢?
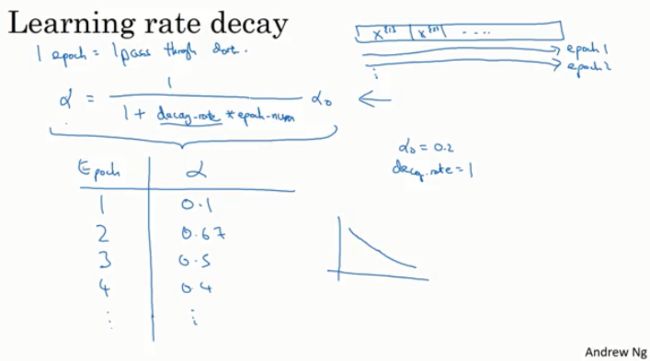
定义α等于1除以1加上某个参数,我把它成为衰减率,再把这个和乘以跌代数作为分母,然后用这个商再乘以初始学习率α0。
这里的衰减率是另一个超参数,也可能需要你再调整。
随着你的迭代函数,你的学习率会根据公式逐渐递减,所以如果你想使用学习率衰减,你可以尝试不同的超参数组合,找到一个效果最好的数值。
除了学习率衰减的公式之外,人们还会使用一些其他方式:
指数级速度让学习率衰减;以离散的阶梯衰减...
通过公式来让学习率α随着时间推移而发生变化,有时候人们还会使用手动衰减:
如果你在一段时间,例如几个小时或者几天来训练一组数据时,可以先对模型进行多天的观察,然后看起来学习率像是减慢了,我就可以降低α,这种手动控制的方式也是可行的。这只有在训练少数样本时是可行的。
现在你有更多的选择如何控制阿尔法学习率,这么多超参数,如何在不同的选项中做出选择呢?
对于我来说,学习率衰减通常在我尝试的事情中比较靠后的位置,设置一个固定的α,还要使它优化的良好,对结果是有很大影响的。它确实对于优化算法是有帮助的,但是我将它的尝试放在比较靠后的位置。
如何更系统的安排所有的超参数方式?以及如何有效的在其中搜索?
神经网络中的局部最优解和鞍点?这样就能够对不同的优化算法所适用的问题有更好的感觉。
第十课:局部最优的问题
陷入局部最优问题。
如何看待局部最优以及深度学习中的优化问题?
如果你在训练一个神经网络,代价函数中大部分梯度为零的点实际上并不是存在很多局部最优,而是鞍点。
从经验上来说,一个高维空间的函数,如果梯度为零,则在每个方向上,它可能是凸函数,也可能是凹函数,假设在一个2万维的空间内,如果一个点要成为局部最优,则需要2万个方向都向上,这种事发生的概率极低。
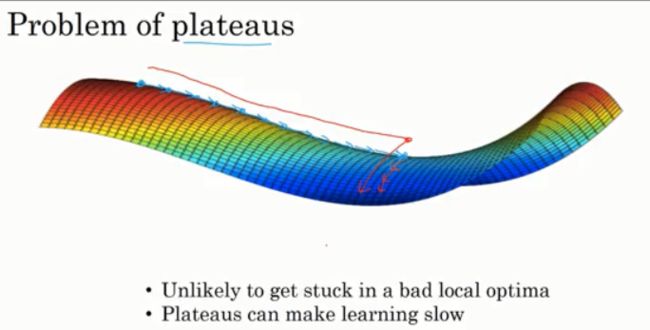
所以实际情况是并非所有的函数图像都向上弯曲,这就是为什么在高维空间中,你更可能碰到像右图这样的鞍点,而不是局部最优。
即在我们在低维空间内的大部分直观感受事实上并不适用于我们的深度学习算法所应用的那些高维空间。
那么问题在哪呢?
真正会降低学习速度的实际上是停滞区。停滞区指的是:导数长时间接近于0的一段区域,因为梯度接近于0,所以在停滞区中你会缓慢的在停滞去区内前进,最终才能逃离这片区域。
总结:
首先:实际上你不太可能陷入糟糕的局部最优点,只要你训练的是一个较大的神经网络,有很多参数,代价函数J在一个相对高维的空间内上。
其次:停滞区是个问题,它会让学习过程变得相当慢,这也是动量算法或RMSprop算法或Adam算法能改善你的学习算法的地方。
比如Adam算法可以加快停滞区向下移动离开停滞区的速度。