强化学习基础——bandit

目录

为选择而生

为错误买单代价

经典方法

朴素Bandit算法

ε-Greedy算法

Thompson sampling算法

Thompson sampling算法流程

UCB

UCB算法流程

LinUCB

Context Bandit-附加信息刻画决策过程

Context Bandit如何学习

LinUCB算法流程

LinUCB代码

LinUCB with Hybrid Linear Models

Hybrid LinUCB算法流程

Hybrid LinUCB代码

---

曾经有一份真挚的感情摆在我的面前我没有珍惜，等我失去的时候才追悔莫及，人间最痛苦的事莫过于此。人生面临很多抉择，虽不如大话西游生死离别，却也让人头疼。如何寻找一条快捷通往华山之路呢？

为选择而生

一个赌徒，要去摇老虎机，走进赌场一看，一排老虎机，外表一模一样，但是每个老虎机吐钱的概率可不一样，他不知道每个老虎机吐钱的概率分布是什么，那么每次该选择哪个老虎机可以做到最大化收益呢？这就是多臂赌博机问题 ( Multi-armed bandit problem, K-armed bandit problem, MAB )。

解决这个问题最好的办法是去试（探索阶段），但不是盲目地试，而是有策略（利用阶段）地快速试一试，这些策略就是Bandit算法。

探索阶段 (Exploration)：通过多次试错推断出选择是否正确的概率。
利用阶段 (Exploitation)：已知所有的选择正确的概率，该如何决策？

核心问题：什么时候探索(Exploration)，什么时候利用 (Exploitation)?

Exploration的代价是要不停的试错，试错成本高，但有助于更加准确的估计选择的概率；
Exploitation会基于目前的估计拿出“最好的”选择，但目前的估计可能是不准的（因为试错依然不够多）。

为错误买单代价

Bandit算法需要量化一个核心问题：探索成本有多大？能不能少为错误买单？

通常使用累积遗憾(regret) 来衡量不同 Bandit 算法在解决多臂问题上的效果。

是第i次试验时被选中臂的期望收益，是所有臂中最优的那个，如果上帝提前告诉我们，我们当然每次试验都选它，问题是上帝不告诉我们。这个公式可以用来对比不同 Bandit 算法的效果：对同样的多臂问题，用不同的 Bandit 算法试验相同次数，看看谁的regret增长得慢。

经典方法

朴素Bandit算法

先随机试若干次，计算每个臂的平均收益，一直选均值最大那个臂。这个算法是人类在实际中最常采用的，不可否认，它还是比随机乱猜要好。

ε-Greedy算法

贪婪策略：

• 以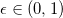概率选择探索，并根据反馈更新概率；
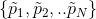• 以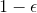概率选择利用，从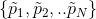中选择概率最高的做决策；

的值可以控制对Exploit和Explore的偏好程度。越接近0，越保守，只想固守而不想选择探索。

同样其缺点也是明显的：

• 在试错次数相同的情况下，good和bad的概率是一样的；
• 在估计的成功概率相同的情况下，good和bad得到再试吃的概率是一样的；

Thompson sampling算法

good choice概率是一个客观存在的、固定的值，可以用一个概率分布来描述的不确定性。随着样本的增加，这个概率分布在真实附近的概率密度会越来越大。

再来看，以概率p = 描述good(reward=1)，以概率p = 描述bad(reward=0)，这是一个典型的Bernoulli (伯努利)分布。

Bayesian学派会用概率分布来描述不确定性：

的选取直接决定了的函数形式，在贝叶斯统计中，

经常和分布一起使用（称为共轭分布），：

会得到一个新的分布：

• 如果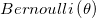的结果为1，则会得到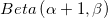
• 如果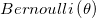的结果为0，则会得到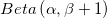

beta分布可以看作一个概率的概率分布，对二项分布中成功概率p的概率分布的描述。

Thompson sampling算法流程

• 用刻画good choice的概率，得到；
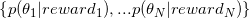• 对每个choice 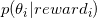随机抽取一个样本，得到；
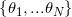• 推荐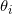最大的choice，得到；
• 更新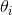的分布：；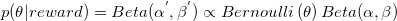

UCB

item被试错k次，计算item选择概率：

当k趋于正无穷时，会趋近于item选择真实概率p；
现实中item被试错概率不可能趋于无穷大，因此估计出item收益概率和真实收益概率总会存在一个差值，即
对某个item尝试的次数越多，对该item回报估计的置信区间越窄、估计的不确定性降低，那些均值更大的item倾向于被多次选择，这是算法保守的部分（exploitation）；对某个item的尝试次数越少，置信区间越宽，不确定性较高，置信区间较宽的item倾向于被多次选择，这是算法激进的部分（exploration）。

总是乐观地认为每道菜能够获得的回报是，这便是著名的Upper Confidence Bound (UCB) 算法。

假设是在[0,1]之间独立随机变量，则

其中，表示样本均值，表示分布均值。

当时，其中T表示由T个user，n表示choice次数。可以得到：

也就是说：

是以概率成立的。

UCB算法流程

初始化：先对每个item都试一遍；
按照如下公式计算每个item的概率，然后选择概率最大的item作为选择：

公式反映均值越大，标准差越小，被选中的概率会越来越大，同时哪些被选次数较少的臂也会得到试验机会。

与ε-Greedy算法相比，这种策略的好处在于：

• 考虑了回报均值的不确定性，让新的item更快得到尝试机会，将探索+开发融为一体；
• 基础的UCB算法不需要任何参数，因此不需要考虑如何验证参数（ε如何确定）的问题；

UCB算法的缺点：

• UCB算法需要首先尝试一遍所有item，因此当item数量很多时是一个问题；
• 一开始各item选择次数都比较少，导致得到的回报波动较大（经常选中实际比较差的item）；

LinUCB

将item看成是独立的个体，缺乏用附加信息刻画决策过程的机制（item的属性、用户画像、交互上下文）：
忽略了item的属性，item类型、标签等；
忽略了用户之间的偏好差别用户可以用年龄、性别来刻画，不同的用户的偏好是不一样的；
忽略了用户选择item的偏好上下文、时间常常是不同的；

Yahoo!的科学家们在2010年发表了A Contextual-Bandit Approach to Personalized News Article Recommendation，利用context信息刻画决策过程，称之为LinUCB。

Context Bandit-附加信息刻画决策过程

在Context bandit中，每次决策由item属性、用户画像、时间、地点上下文决定：

• 观测到特征向量x=(item类型，item标签，男，女，年龄，时间，地域)；
• 预测用户是否选择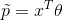：，其中是要学习系数；
• 对所有item进行预测得到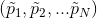选择；

Context Bandit如何学习

在context bandit中，使用的线性回归－Ridge Regression来求解。

输入：多次实验结果

优化目标如下：

其中，是N次观测组成特征矩阵，是N次实验结果，也就是常用的L2 normalization，防止过拟合。

为了求解，对求导：

得到

估计出item概率和真实概率总会存在一个差值，即。总是乐观地认为每道菜能够获得的回报是。在MAB中，是通过Chernoff-Hoeffding Bound得到的，reward是在[0, 1]之间独立同分布的。在Context Bandit中，类似Chernoff-Hoeffding Bound的定理来量化，如下：

。

LinUCB算法流程

LinUCB代码

def update(reward):
    if reward == -1:
        return
    elif reward == 1:
        r = r1
    elif reward == 0:
        r = r2

    Aa[max_a] += np.outer(x, x)
    Aa_inv[max_a] = np.linalg.inv(Aa[max_a])
    ba[max_a] += r * x
    theta[max_a] = Aa_inv[max_a].dot(ba[max_a])


def recommend(time, user_features, choices):
    global max_a
    global x

    article_len = len(choices)

    x = np.array(user_features).reshape((d, 1))
    x_t = np.transpose(x)
    index = [index_all[article] for article in choices]
    UCB = np.matmul(np.transpose(theta[index], (0, 2, 1)), x) + alpha * np.sqrt(np.matmul(x_t, Aa_inv[index].dot(x)))

    max_index = np.argmax(UCB)
    max_a = index[max_index]
    return choices[max_index]

LinUCB with Hybrid Linear Models

在很多系统中，各个arm之间会有一部分共享参数，每个arm有独立参数。比如在推荐系统问题中，关于用户和当前时间的feature可以共享参数，每个ar的参数则互相独立。在这个定义下，我们仍然把独立部分的参数定义为，并定义共享部分参数为，则：

其中，是user和item交叉特征，是所有arm系数矩阵。

Hybrid LinUCB算法流程

Hybrid LinUCB代码

    def update(self, reward):
        if reward == -1:
            pass
        elif reward == 1 or reward == 0:
            if reward == 1:
                r = self.r1
            else:
                r = self.r0

            self.A0 += self.BaT[self.a_max].dot(self.AaIBa[self.a_max])
            self.b0 += self.BaT[self.a_max].dot(self.AaIba[self.a_max])
            self.Aa[self.a_max] += np.dot(self.xa, self.xaT)
            self.AaI[self.a_max] = np.linalg.inv(self.Aa[self.a_max])
            self.Ba[self.a_max] += np.dot(self.xa, self.zT)
            self.BaT[self.a_max] = np.transpose(self.Ba[self.a_max])
            self.ba[self.a_max] += r * self.xa
            self.AaIba[self.a_max] = np.dot(self.AaI[self.a_max], self.ba[self.a_max])
            self.AaIBa[self.a_max] = np.dot(self.AaI[self.a_max], self.Ba[self.a_max])

            self.A0 += np.dot(self.z, self.zT) - np.dot(self.BaT[self.a_max], self.AaIBa[self.a_max])
            self.b0 += r * self.z - np.dot(self.BaT[self.a_max], self.AaIba[self.a_max])
            self.A0I = np.linalg.inv(self.A0)
            self.A0IBaTAaI[self.a_max] = self.A0I.dot(self.BaT[self.a_max]).dot(self.AaI[self.a_max])
            # self.AaIBaA0IBaTAaI[self.a_max] = np.matmul(self.AaIBa[self.a_max], self.A0IBaTAaI[self.a_max])
            self.beta = np.dot(self.A0I, self.b0)
            self.theta = self.AaIba - np.dot(self.AaIBa, self.beta)

        else:
            pass

    def recommend(self, timestamp, user_features, articles):
        article_len = len(articles)  # 20

        self.xa = np.array(user_features).reshape((self.d, 1))  # (6,1)
        self.xaT = np.transpose(self.xa)  # (1,6)

        index = [self.index_all[article] for article in articles]
        article_features_tmp = self.article_features[index]

        # za : feature of current user/article combination, k*1
        za = np.outer(article_features_tmp.reshape(-1), self.xa).reshape((article_len, self.k, 1))  # (20,36,1)
        zaT = np.transpose(za, (0, 2, 1))  # (20,1,36)

        A0Iza = np.matmul(self.A0I, za)  # (20,36,1)
        A0IBaTAaIxa = np.matmul(self.A0IBaTAaI[index], self.xa)  # (20,36,1)
        AaIxa = self.AaI[index].dot(self.xa)  # (20,6,1)
        AaIBaA0IBaTAaIxa = np.matmul(self.AaIBa[index], A0IBaTAaIxa)  # (20,6,1)
        # AaIBaA0IBaTAaIxa = np.matmul(self.AaIBaA0IBaTAaI[index], self.xa) # (20,6,1)

        s = np.matmul(zaT, A0Iza - 2 * A0IBaTAaIxa) + np.matmul(self.xaT, AaIxa + AaIBaA0IBaTAaIxa)  # (20,1,1)
        p = zaT.dot(self.beta) + np.matmul(self.xaT, self.theta[index]) + self.alpha * np.sqrt(s)  # (20,1,1)
        # assert (s < 0).any() == False
        # assert np.isnan(np.sqrt(s)).any() == False

        # print A0Iza.shape, A0IBaTAaIxa.shape, AaIxa.shape, AaIBaA0IBaTAaIxa.shape, s.shape, p.shape (for debugging)
        max_index = np.argmax(p)
        self.z = za[max_index]
        self.zT = zaT[max_index]
        art_max = index[max_index]
        self.a_max = art_max  # article index with largest UCB

        return articles[max_index]