NLP实践三:特征选择
目录
- TF-IDF
- TF-IDF原理
- TF-IDF实践
- 互信息
- 互信息计算
- 参考链接
TF-IDF
TF-IDF原理
TF-IDF(Term Frequency-Inverse DocumentFrequency, 词频-逆文件频率)。TF-IDF是一种统计方法,用以评估一字词对于一个文件集或一个语料库中的其中一份文件的重要程度。字词的重要性随着它在文件中出现的次数成正比增加,但同时会随着它在语料库中出现的频率成反比下降。
词频TF(item frequency):某一给定词语在该文本中出现次数。该数字通常会被归一化(分子一般小于分母),以防止它偏向长的文件,因为不管该词语重要与否,它在长文件中出现的次数很可能比在段文件中出现的次数更大。
词 频 ( T F ) = 某 个 词 在 文 章 中 出 现 次 数 文 章 总 词 数 词频(TF)=\frac{某个词在文章中出现次数}{文章总词数} 词频(TF)=文章总词数某个词在文章中出现次数
逆向文件频率IDF(inverse document frequency):一个词语普遍重要性的度量。主要思想是:如果包含词条t的文档越少, IDF越大,则说明词条具有很好的类别区分能力。某一特定词语的IDF,可以由总文件数目除以包含该词语之文件的数目,再将得到的商取对数得到。
逆 文 档 频 率 ( I D F ) = l o g ( 语 料 库 的 文 档 总 数 包 含 该 词 的 文 档 数 + 1 ) 逆文档频率(IDF)=log(\frac{语料库的文档总数}{包含该词的文档数+1}) 逆文档频率(IDF)=log(包含该词的文档数+1语料库的文档总数)
T F − I D F = 词 频 ( T F ) × 逆 文 档 频 率 ( I D F ) TF-IDF=词频(TF)\times 逆文档频率(IDF) TF−IDF=词频(TF)×逆文档频率(IDF)
示例:假如一篇文件的总词语数是100个,而词语“母牛”出现了3次,那么“母牛”一词在该文件中的词频就是3/100=0.03。一个计算文件频率 (DF) 的方法是测定有多少份文件出现过“母牛”一词,然后除以文件集里包含的文件总数。所以,如果“母牛”一词在1,000份文件出现过,而文件总数是10,000,000份的话,其逆向文件频率就是 log(10,000,000 / 1,000)=4。最后的TF-IDF的分数为0.03 *4=0.12。
TF-IDF实践
import pickle
from sklearn.feature_extraction.text import TfidfVectorizer,CountVectorizer
test= pickle.load(open("test.pickle","rb"))
all_content = test["content"].apply(lambda x:" ".join(x))
all_content.head()
tf_vectorizer =TfidfVectorizer(binary=True,strip_accents='unicode',max_features=10000).fit(all_content.head())
listOfWords = tf_vectorizer.get_feature_names()
tf_vectorizer.transform(all_content.head())
X_test = tf_vectorizer.transform(all_content.head())
X_test.shape
print(X_test)
互信息
在概率论和信息论中,两个随机变量的互信息(Mutual Information,简称MI)或转移信息(transinformation)是变量间相互依赖性的量度。不同于相关系数,互信息并不局限于实值随机变量,它更加一般且决定着联合分布 p(X,Y) 和分解的边缘分布的乘积 p(X)p(Y) 的相似程度。互信息(Mutual Information)是度量两个事件集合之间的相关性(mutual dependence)。互信息是点间互信息(PMI)的期望值。互信息最常用的单位是bit。
两个离散随机变量 X 和 Y 的互信息可以定义为:
I ( X ; Y ) = ∑ y ∈ Y ∑ x ∈ X p ( x , y ) log ( p ( x , y ) p ( x ) p ( y ) ) I(X ; Y)=\sum_{y \in Y} \sum_{x \in X} p(x, y) \log \left(\frac{p(x, y)}{p(x) p(y)}\right) I(X;Y)=y∈Y∑x∈X∑p(x,y)log(p(x)p(y)p(x,y))
其中 p(x,y) 是 X 和 Y 的联合概率分布函数,而p(x)和p(y)分别是 X 和 Y 的边缘概率分布函数。
在连续随机变量的情形下,求和被替换成了二重定积分:
I ( X ; Y ) = ∫ Y ∫ X p ( x , y ) log ( p ( x , y ) p ( x ) p ( y ) ) d x d y I(X ; Y)=\int_{Y} \int_{X} p(x, y) \log \left(\frac{p(x, y)}{p(x) p(y)}\right) d x d y I(X;Y)=∫Y∫Xp(x,y)log(p(x)p(y)p(x,y))dxdy
其中 p(x,y) 当前是 X 和 Y 的联合概率密度函数,而p(x)和p(y)分别是 X 和 Y 的边缘概率密度函数。
互信息量I(xi;yj)在联合概率空间P(XY)中的统计平均值。 平均互信息I(X;Y)克服了互信息量I(xi;yj)的随机性,成为一个确定的量。如果对数以 2 为基底,互信息的单位是bit。
直观上,互信息度量 X 和 Y 共享的信息:它度量知道这两个变量其中一个,对另一个不确定度减少的程度。例如,如果 X 和 Y 相互独立,则知道 X 不对 Y 提供任何信息,反之亦然,所以它们的互信息为零。在另一个极端,如果 X 是 Y 的一个确定性函数,且 Y 也是 X 的一个确定性函数,那么传递的所有信息被 X 和 Y 共享:知道 X 决定 Y 的值,反之亦然。因此,在此情形互信息与 Y(或 X)单独包含的不确定度相同,称作 Y(或 X)的熵。而且,这个互信息与 X 的熵和 Y 的熵相同。(这种情形的一个非常特殊的情况是当 X 和 Y 为相同随机变量时。)
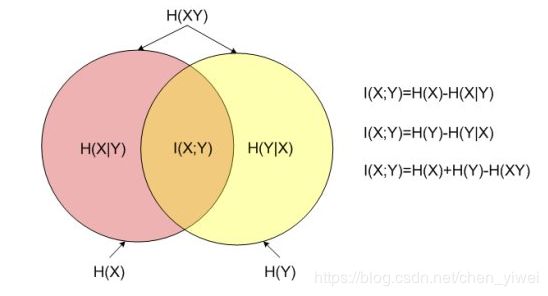
I ( X ; Y ) = H ( X ) − H ( X ∣ Y ) = H ( Y ) − H ( Y ∣ X ) = H ( X ) + H ( Y ) − H ( X , Y ) = H ( X , Y ) − H ( X ∣ Y ) − H ( Y ∣ X ) \begin{aligned} I(X ; Y) &=H(X)-H(X | Y) \\ &=H(Y)-H(Y | X) \\ &=H(X)+H(Y)-H(X, Y) \\ &=H(X, Y)-H(X | Y)-H(Y | X) \end{aligned} I(X;Y)=H(X)−H(X∣Y)=H(Y)−H(Y∣X)=H(X)+H(Y)−H(X,Y)=H(X,Y)−H(X∣Y)−H(Y∣X)
其中H(X)和H(Y) 是边缘熵,H(X|Y)和H(Y|X)是条件熵,而H(X,Y)是X和Y的联合熵。注意到这组关系和并集、差集和交集的关系类似,用Venn图表示
互信息计算
label =test["label"]
label_id = dict(zip(list(set(label.head())),range(len(set(label.head())))))
from sklearn import metrics as mr
import numpy as np
label_num =[]
for each in label.head():
label_num.append(label_id[each])
X_test_F = X_test.toarray()
X_test_T=X_test_F.T
feature = {}
label_num = np.array(label_num)
for i in range(X_test_T.shape[0]):
feature[i] = mr.mutual_info_score(label_num,X_test_T[i])
参考链接
互信息