迪杰斯特拉(Dijkstra)算法 - 解决最短路径问题
迪杰斯特拉算法比较不好理解,我们来先看一个问题:
看一个应用场景和问题:
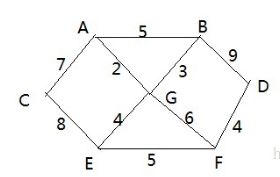
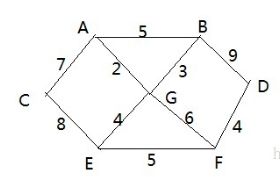
- 战争时期,胜利乡有7个村庄(A, B, C, D, E, F, G) ,现在有六个邮差,从G点出发,需要分别把邮件分别送到 A, B, C , D, E, F 六个村庄
- 各个村庄的距离用边线表示(权) ,比如 A – B 距离 5公里
- 问:如何计算出G村庄到 其它各个村庄的最短距离?
- 如果从其它点出发到各个点的最短距离又是多少?
-
迪杰斯特拉(Dijkstra)算法介绍
迪杰斯特拉(Dijkstra)算法是典型最短路径算法,用于计算一个结点到其他结点的最短路径。 它的主要特点是以起始点为中心向外层层扩展(广度优先搜索思想),直到扩展到终点为止。 -
迪杰斯特拉(Dijkstra)算法过程
设置出发顶点为v,顶点集合V{v1,v2,vi…},v到V中各顶点的距离构成距离集合Dis,Dis{d1,d2,di…},Dis集合记录着v到图中各顶点的距离(到自身可以看作0,v到vi距离对应为di)1.从Dis中选择值最小的di并移出Dis集合,同时移出V集合中对应的顶点vi,此时的v到vi即为最短路径
2.更新Dis集合,更新规则为:比较v到V集合中顶点的距离值,与v通过vi到V集合中顶点的距离值,保留值较小的一个(同时也应该更新顶点的前驱节点为vi,表明是通过vi到达的)
3.重复执行两步骤,直到最短路径顶点为目标顶点即可结束
看上面的过程很难理解迪杰斯特拉。现在我用自己的话来通俗的讲下:
- 迪杰斯特拉算法的第一步就是先创建3个数组或集合分别用来记录已访问的顶点(用V表示),出发顶点到其余各顶点的距离(用D表示),和各顶点的前驱顶点(用P表示)
- 上面做好之后从出发顶点开始(如上图中的G就是出发顶点),遍历出发顶点到其余各个顶点的距离(不直达可以用一个较大的整数表示),然后把这些信息记录到第一步的3个数组或者集合中。
- 第三步,从第一步的记录距离的集合中选取一个没有被访问顶点且距离最小的顶点开始,继续遍历该顶点(如:顶点n,下面以n举例)到其他顶点(比如:下标为m的顶点,下面以m举例)的距离(已访问过的顶点除外)。得到从该顶点到
- 接着第3步,如果: 出发顶点到m的距离 + 从m到n的距离 > 从出发顶点到n的距离(也就是距离表记录的距离) ,那么就把:出发顶点到m的距离 + 从m到n的距离 更新到距离表中,表示从出发顶点到n顶点的距离最小,同时更新第一步中的V数组和P数组(更新n为已访问顶点,更新m的前驱为n)
- 重复第3步和第4步,直到把集合V都更新为已访问为止。
- 这样的描述也许不是很明白,可以参考下面的代码加深理解
代码示例:
实现文章开头的例子,代码都要详细注释
定义一个图类描述村庄图(必须先要学数据结构 - 图)
// 图
public class Graph {
// 图的顶点
private char[] vertex;
// 图的边,邻接矩阵表示
private int[][] weight;
public Graph(char[] vertex, int[][] weight) {
this.vertex = vertex;
this.weight = weight;
}
public char[] getVertex() {
return vertex;
}
public void setVertex(char[] vertex) {
this.vertex = vertex;
}
public int[][] getWeight() {
return weight;
}
public void setWeight(int[][] weight) {
this.weight = weight;
}
}
迪杰斯特拉算法核心算法类
/**
* 迪杰斯特拉算法
*/
public class DijkstraAlgorithm {
// 记录各顶点是否访问过,数组的下标对应各顶点的下标,0:没有被访问过,1:已被访问过
private int[] isVisited;
// 记录出发顶点到各顶点的距离,10000表示不可直达,
private int[] distance;
// 与distance对应,该数组的下标对应顶点的下标,数组的值表示该顶点的前驱顶点
// 如:出发顶点为G,G到A的最短距离是2,然后在从A到B的距离是3,那么A的前驱是G
private int[] pre_index;
// 图
private Graph graph;
/**
*
* @param graph 图对象
*/
public DijkstraAlgorithm(Graph graph) {
this.graph = graph;
int vertexLength = graph.getVertex().length;
isVisited = new int[vertexLength];
distance = new int[vertexLength];
// distance的距离都要设为最大值
Arrays.fill(distance, 10000);
pre_index = new int[vertexLength];
// 把顶点的前驱都设置为-1
Arrays.fill(pre_index, -1);
}
/**
*
* @param index 出发顶点的下标
*/
public void dijkstra(int index) {
if (graph == null){
return;
}
// 设置出发顶点的访问距离为0
this.distance[index] = 0;
// 开始更新数据
update(index);
for (int j = 1; j < graph.getVertex().length; j++) {
// 获取新的访问顶点
int visitVertex = getNewVisitVertex();
// 从开始新的顶点访问
update(visitVertex);
}
}
/**
* 下标index开始访问,开始更新对应的数据
* @param index
*/
private void update(int index) {
// 先把index设置为已访问
isVisited[index] = 1;
// 定义变量len,用来记录从出发顶点到对应顶点的距离
int len = 0;
// 变量顶点index到其他顶点的距离
for (int i = 0; i < graph.getWeight()[index].length; i++) {
// 出发顶点到index的距离+从index到i的距离
len = distance[index] + graph.getWeight()[index][i];
// 如果顶点i没有被访问过并且从出发顶点到i的直连距离 > 出发顶点到index的距离+从index到i的距离
if (isVisited[i] != 1 && len < distance[i]) {
// 满足判断就开始更新
// 先更新该顶点到i的距离
distance[i] = len;
// 更新i的前驱为index
pre_index[i] = index;
}
}
}
/**
* 获取新的开始访问顶点
* @return
*/
private int getNewVisitVertex() {
int index = 0;
int min = 10000;
for (int i = 0; i < distance.length; i++) {
// 如果该顶点没有被访问过,
if (isVisited[i] == 0 && distance[i] < min) {
min = distance[i];
index = i;
}
}
// for循环结束,找到了新的访问顶点
return index;
}
// 打印最后的结果
public void print() {
for (int i = 0; i < distance.length; i++) {
System.out.println("顶点 " + graph.getVertex()[i] + " 到出发顶点的距离:" + distance[i]);
}
System.out.println("==============================");
for (int j = 0; j < pre_index.length; j++) {
if (pre_index[j] != -1){
System.out.println("顶点 " + graph.getVertex()[j] + " 的前驱顶点是:" + graph.getVertex()[pre_index[j]]);
}else {
System.out.println("顶点 " + graph.getVertex()[j] + " 的前驱顶点是:没有前驱节点" );
}
}
}
}
测试类
public class MyTest {
public static void main(String[] args) {
char[] vertex = { 'A', 'B', 'C', 'D', 'E', 'F', 'G' };
//邻接矩阵
int[][] matrix = new int[vertex.length][vertex.length];
final int N = 10000;// 表示不可以连接
matrix[0]=new int[]{N,5,7,N,N,N,2};
matrix[1]=new int[]{5,N,N,9,N,N,3};
matrix[2]=new int[]{7,N,N,N,8,N,N};
matrix[3]=new int[]{N,9,N,N,N,4,N};
matrix[4]=new int[]{N,N,8,N,N,5,4};
matrix[5]=new int[]{N,N,N,4,5,N,6};
matrix[6]=new int[]{2,3,N,N,4,6,N};
// 创建图对象
Graph graph = new Graph(vertex, matrix);
// 创建迪杰斯特拉对象
DijkstraAlgorithm dijkstraAlgorithm = new DijkstraAlgorithm(graph);
dijkstraAlgorithm.dijkstra(6);
// 打印最后的结果
dijkstraAlgorithm.print();
}
}
运行结果(打印输出distance和pre_index即可得到结果):
顶点 A 到出发顶点的距离:2
顶点 B 到出发顶点的距离:3
顶点 C 到出发顶点的距离:9
顶点 D 到出发顶点的距离:10
顶点 E 到出发顶点的距离:4
顶点 F 到出发顶点的距离:6
顶点 G 到出发顶点的距离:0
==============================
顶点 A 的前驱顶点是:G
顶点 B 的前驱顶点是:G
顶点 C 的前驱顶点是:A
顶点 D 的前驱顶点是:F
顶点 E 的前驱顶点是:G
顶点 F 的前驱顶点是:G
顶点 G 的前驱顶点是:没有前驱节点
- 对上图看,G为出发顶点,看输出结果,我们来看C与G的距离是9,,在看前驱表的输出,C的的前驱顶点是A,而A的前驱顶点G,即得出从G到C的最短路径为9,走的路径是先从G到A,在从A到C即为G到C的最短路径。
- 输出结果很明了的得到G到各个点的最短路径。这就是迪杰斯特拉算法
- 迪杰斯特拉算法是广度优先搜索思想,从开始顶点开始,最近到远,层层的向外扩散