前置芝士
了解普通并查集及普通并查集的数据压缩。以下为普通的数据压缩并查集写法:
const int N = 1e5 + 5;
int n, fa[N];
void find (int x) { //寻找祖先
if (fa[x] == x)
return x;
return fa[x] = find (fa[x]);
}
void unions (int x, int y) { //合并两个节点
int xx = find (x), yy = find (y);
if (xx == yy)
return ;
fa[xx] = yy;
return ;
}
普通并查集只能求出节点之间的连接关系,多用于判断节点之间的连通性,但对于节点之间的其他关系(如距离)则无从下手。
这时候,我们有一个很自然的想法:将普通并查集中的边附上权值。
如果不考虑路径压缩和合并点,则只需要记录每个点到父节点的路径长度就可以看。但是如果进行路径压缩和合并操作,则需要对点与点之间除连通性以外的关系做特殊处理。
路径压缩
给出一个简单的模型:

若要将点D连接到点A,则点A到点D的距离应保持不变,即 \(val2+val3\) :
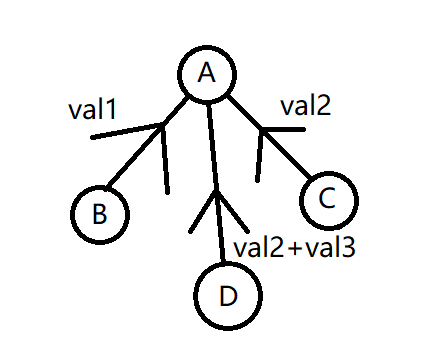
得到结论:带权并查集进行路径压缩的时候,当前节点到根节点的距离应为 父节点到根节点的距离+当前节点到父节点的距离。
合并操作
普通并查集进行两点(以下设两节点为 \(x,y\) ,合并权值为 \(val1\))合并的方式,是连接此两点的两个祖父节点(以下设两祖父节点为 \(px,py\) )。
普通并查集连接边时不用考虑权值问题,所以可以直接将 \(py\) 点的父节点更改为 \(px\) 节点。但带权并查集还要求出 \(py\) 到 \(px\) 的权值。
合并问题可以简化成如下的模型:
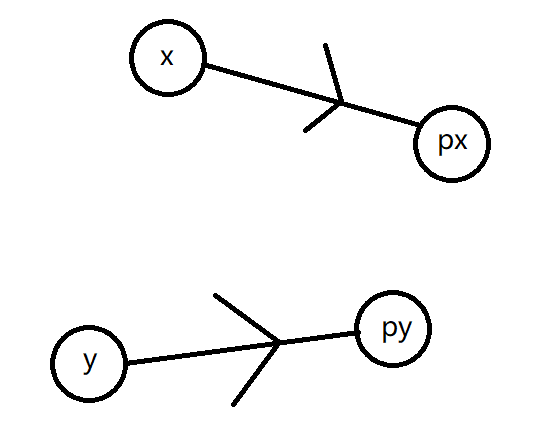
假设我们先将 \(x\) 与 \(y\) 连接起来:
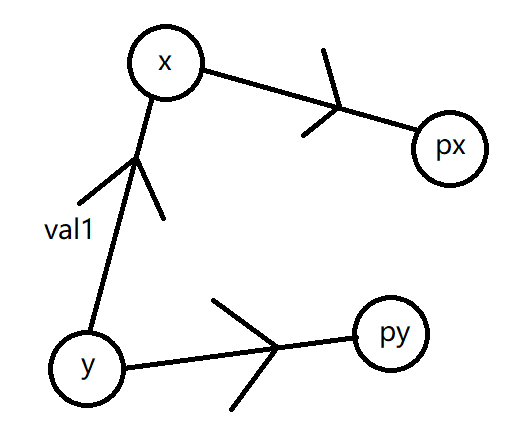
则可以得出,\(y\) 到 \(px\) 的距离应为 \(val1 + (x到px的距离)\)。若拆掉 \(y→x\) 的边,添加 \(py→px\) 的边,则 \(y\) 到 \(px\) 的距离还应为 \(val1 + (x到px的距离)\)。
显然:\((py→px) + (y→py) = val1 + (x到px的距离)\)。
即:\((py→px) = val1 + (x到px的距离) - (y→x)\)
由此得到如何求 \(py\) 到 \(px\) 的权值。
板子代码
const int N = 1e5 + 5;
int n, fa[N], val[N]; //val[x]=x节点到父节点的距离
void find (int x) { //寻找祖先
if (fa[x] == x)
return x;
int t = fa[x];
fa[x] = find (fa[x]);
val[x] += val[t];
return ;
}
void unions (int x, int y, int v) { //合并两个节点
int xx = find (x), yy = find (y);
if (xx == yy)
return ;
fa[xx] = yy;
val[xx] = -val[x] + val[y] + v;
return ;
}
例题
HDU3038 How Many Answers Are Wrong
题目大意
有 \(n\) 个整数(包括负数和0),不知道每个数的具体值,但是会给定 \(m\) 次某两个下标范围内的数值的和。求 \(m\) 次中,与前面给出的条件自相矛盾的次数。
解法
设每次给定的区间范围为 \(l,r\) ,区间和为 \(val\) ;
首先可以得到一个命题:能够确认为自相矛盾的情况,只有 “明确出现了从前面给定的已知合理条件中,可以得出 \(l\) 到 \(r\) 的区间和,并且该区间和与 \(val\) 不相等。”
若考虑进行前缀和预处理,则会发现本题中判断自相矛盾的方式与带权并查集的端点合并操作有着异曲同工之妙。但是若直接将该区间的左端点和右端点连接起来并附上权值,会出现 “区间和包括端点和” 的问题。
解决办法是将 \(l-1\) 和 \(r\) 连接起来并附上区间和,而不是 \(l\) 和 \(r\)。
(看心情补详细图解)
代码
(注意HDU和POJ不支持使用 #include )
#include
using namespace std;
const int N = 2e5 + 5;
int n, m, ans, fa[N], val[N];
int find (int x) {
if (fa[x] == x)
return x;
int t = fa[x];
fa[x] = find (fa[x]);
val[x] += val[t];
return fa[x];
}
void unions (int x, int y, int v) {
int xx = find (x), yy = find (y);
fa[xx] = yy;
val[xx] = -val[x] + val[y] + v;
return ;
}
int main () {
while (scanf ("%d%d", &n, &m) != EOF) {
for (int i = 0; i <= n; i ++) {
fa[i] = i;
val[i] = 0;
}
ans = 0;
for (int i = 1; i <= m; i ++) {
int l, r, sum;
scanf ("%d%d%d", &l, &r, &sum);
l --;
int x = find (l), y = find (r);
if (x == y) {
if (val[l] - val[r] != sum)
ans ++;
} else
unions (l, r, sum);
}
printf ("%d\n", ans);
}
return 0;
}