资源调度问题——贪心算法
资源调度:给定等待服务的客户集合A = {1, 2, …, n},预计对客户i的服务时间是ti,该客户希望的完成时间是di,即T = {t1, t2,…, tn},D = {d1, d2,…, dn}。如果对客户i的服务在di之前结束,那么对客户i的服务没有延迟;如果在di之后结束,那么这个服务就被延迟了,延迟的时间等于该服务时间减去di。假设都是ti和di正整数,一个调度是函数f:A→N,其中是对客户i的服务开始的时间,要求所有区间互不重叠。一个调度f的最大延迟是所有客户延迟时间的最大值,例如:
A ={1, 2, 3, 4, 5}
T= {5, 8, 4, 10, 3}
D = {10, 12 , 15, 11,20}
那么对于调度f1
f1:{1, 2, 3, 4, 5} → N
f1(1)= 0, f1(2)= 5, f1(3)= 13, f1(4) = 17, f1(5)= 27
客户1, 2, 3, 4, 5的延迟分别是0, 1, 2, 16, 10;最大延迟是max{0, 1, 2, 16 ,10}= 16。
但是,不同调度的最大延迟是不一样的,再如对同一个实例的另一个调度f2
f2:{1, 2, 3, 4, 5} → N
f2(1)= 0, f2(2)= 15, f2(3) = 23, f2(4) = 5, f2(5) = 27
客户1~5的延迟分别是0, 11, 12, 4 ,10;最大延迟是max{0, 11, 12, 4 ,10}= 12。
上述调度f1和f2的安排分别如图1所示:
![]()
图1 两个不同的调度方案
显然,调度f2比f1具有更小的延迟。
我们的问题是:给定 A = {1, 2, …, n},T= {t1, t2, …, tn}和D = {d1, d2, …, dn},用贪心算法求解具有最小延迟的调度f(不要求给出理论上的正确性证明)。
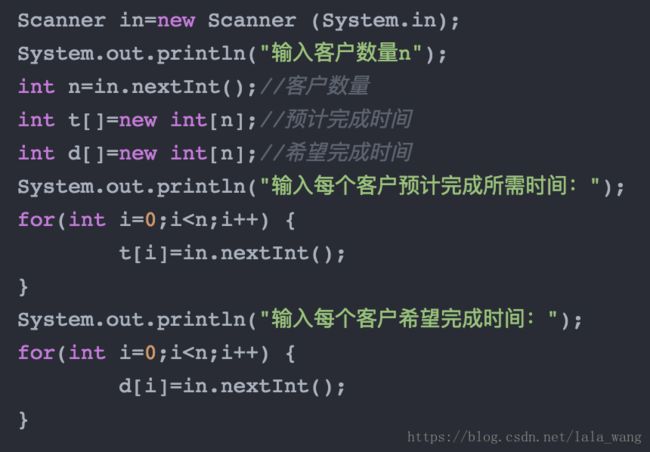
| import java.util.Scanner; |