《Generalized Intersection over Union: A Metric and A Loss for Bounding Box Regression》论文详解

现在在物体检测领域，通常会使用IoU(Intersection over Union)来作为一个很重要的度量指标。但是很多时候在训练网络时，采用的是l2-norm来回归检测框的，文章认为采用l2-norm来训练模型而使用IoU来衡量模型好坏，这两者之间似乎存在着某种不匹配的关系。

举个例子，如下图所示，

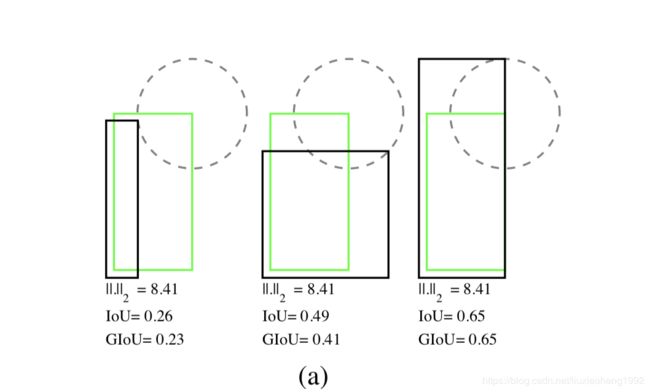
现假设采用左上角右下角的坐标来表示一个矩形框，即$(x_1,y_1,x_2,y_2)$。在采用l2-norm来度量两个框的匹配度，即上图中绿色表示的ground truth框与黑框表示的预测框之间的匹配度，当假设两个框的一个角的欧拉距离是固定的（这里假设两个框的左下角距离固定），那么这两个框在l2-norm度量下的相似度，在当以绿色框右上角为圆形某固定值为半径的圆（黑色虚线表示）上的每个点表示预测框的右上角时，l2-norm值是一样的。
这句话可以用下面公式表示：
绿色框左上角坐标为$(x_1,y_1)$右下角为$(x_2,y_2)$
黑色框左上角坐标为$(x_1^{\prime },y_1^{\prime })$右下角为$(x_2^{\prime },y_2^{\prime })$
下面要满足两个条件，

1. 两个框左下角$(x_1,y_2)$,$(x_1^{\prime },y_2^{\prime })$距离为定值，可以用下面公式表示
   $(x_1-x_1^{\prime }{)}^2+((y_2-y_2^{\prime }{)}^2)=a$
   这里a表示定值
2. 以$(x_2,y_1)$为圆形，某个定值为半径，可以用下面公式表示
   $(x-x_2{)}^2+(y-y_1{)}^2=r^2$
   这里用r表示半径

将上面两式相加就是两个矩形框的l2-norm的表示，可以看出只要取圆上的另一一点，l2-norm的结果是一样的，而这时候IoU和后面要介绍的GIoU值都是不一样的，这就说明了l2-norm不能很好的表示IoU值。而且这个结论与用什么方式表示矩形框是无关的，如下面用矩形框的中心点和框的宽高来表示一个框也可以得到相应的结论。

为了更好的优化网络以及有一个更好的度量，文章提出了GIoU的概念。

一、GIoU的性质

下面先来回顾一下IoU的计算，如下式表示
对于任意两个形状，A和B，它们的IoU为
$IoU=\frac{|A\bigcap B|}{|A\bigcup B|}$
当两个物体没有相交时，IoU定义为0。
IoU具有以下性质，使得IoU在2D、3D计算机视觉中成为一个重要的评测指标：

1. IoU能作为一中度量，而$L_{IoU}=1-IoU$能满足度量的所有性质。
2. IoU对于尺度有不变性。这意味着两个任意形状A和B之间的相似性与它们的空间尺度无关。

然而IoU作为度量也有它的缺点，那就是当$|A\bigcap B|$=0是IoU为0，这时候并不能表示两个物体之间的距离，他们是邻近的还是相距很远的。为了解决这个问题，本文提出GIoU。

先介绍一下GIoU作为一种度量方式，它具有的性质：

1. 类似与IoU，GIoU也能表示距离。$L_{GIoU}=1-GIoU$能满足度量的所有性质。
2. 类似IoU，GIoU也对于尺度有不变性。
3. GIoU是IoU的下界，即$GIoU(A,B)\le IoU(A,B)$，当A和B的形状和位置无限趋近时，等号成立
4. 类似$0\le IoU\le 1$，$-1\le GIoU\le 1$，如果两个物体重叠时$IoU(A,B)=GIoU(A,B)=1$，如果两个物体的并集与包围两个物体的形状之比趋近0时GIoU取得-1。

二、GIoU的计算方式

对于两个框表示
预测框：$B^p=(x_1^p,y_1^p,x_2^p,y_2^p)$
标注框：$B^g=(x_1^g,y_1^g,x_2^g,y_2^g)$

1. 为确保预测框中$x_2^p>x_1^p$,$y_2^p>y_1^p$:
   ${\hat{x}}_1^p=min(x_1^p,x_2^p),{\hat{x}}_2^p=max(x_1^p,x_2^p)$
   ${\hat{y}}_1^p=min(y_1^p,y_2^p),{\hat{y}}_2^p=max(y_1^p,y_2^p)$
2. 标注框的面积为$A^g=(x_2^g-x_1^g)\times (y_2^g-y_1^g)$
3. 预测框的面积为$A^p=(x_2^p-x_1^p)\times (y_2^p-y_1^p)$
4. 两者的交集为
   $x_1^I=max({\hat{x}}_1^p,x_1^g),x_2^I=min({\hat{x}}_2^p,x_2^g)$
   $y_1^I=max({\hat{y}}_1^p,y_1^g),y_2^I=min({\hat{y}}_2^p,y_2^g)$
   $I=\{\begin{array}{l}(x_2^I-x_1^I)\times (y_2^I-y_1^I)if{x}_2^I>x_1^I,x{y}_2^I>y_1^I\\ 0otherwise\end{array}$
5. 计算两个框最小的包围框
   $x_1^c=min({\hat{x}}_1^p,x_1^g),x_2^c=max({\hat{x}}_2^p,x_2^g)$
   $y_1^c=min({\hat{y}}_1^p,y_1^g),y_2^c=max({\hat{y}}_2^p,y_2^g)$
6. 最小的包围框的面积为$A^c=(x_2^c-x_1^c)\times (y_2^c-y_1^c)$
7. $IoU=\frac{I}{U},U=A^p+A^g-I$
8. $GIoU=IoU-\frac{A^c-U}{A^c}$
9. $L_{GIoU}=1-GIoU$
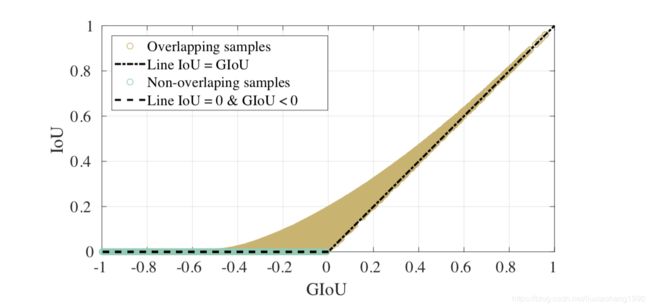
   当IoU为0时在训练网络时没有梯度了，影响训练质量和模型收敛速度，而GIoU不会为0。而且从GIoU的性质3可以看出，GIoU与IoU有很强的相关性。文章也采用了随机的10K个样本求IoU和GIoU得到下图，也可以 看出二者相关性，并且还能看出GIoU相对于IoU能够获得更陡的梯度值，更有利于模型训练。
   

关于GIoU Loss的稳定性
通过前面介绍知道
$0\le L_{IoU}\le 1$，$0\le L_{GIoU}\le 2$
所以两个loss都是有界的

$L_{IoU}$在IoU为0时的行为
当IoU=0时，$L_{GIoU}=2-\frac{U}{A^c}$，要使得loss减小，就要使$U/A^c$增大，从而要使得$U$增大或者$A^c$减小，要达到这种要求就需要预测框和标注框尽量重叠。

关于GIoU实践可能存在的问题
在博主训练yolov3的时候，使用了GIoUloss，不用与smoothL2-loss的计算只要算坐标的一个偏置量的差值，要算GIoUloss必须先求出坐标，而在求坐标的时候使用了e为底的指数，造成了w和h为inf的情况，导致loss为nan，采用的办法是限制w和h为一个较大的值。