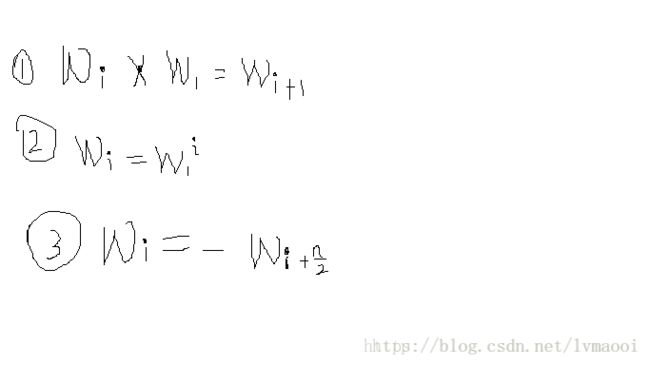FFT(快速傅里叶变换)概述

表示才上高一根本不知道复数是啥，所以复数是啥？？？

所以这篇博客是教你在不懂复数的情况下教你怎么写FFT。

所以FFT是什么？

众所周知，要求两个多项式的乘积，时间复杂度是 n2 n 2 的。FFT可以让我们在 nlogn n l o g n 的时间里求多项式乘积（虽然在 n n 很小的情况下，FFT真的干不过 n2 n 2 ）。

现在介绍一下思想。一个 n n 次多项式可以表示为 n+1 n + 1 个点，也就是多项式的另一种表示方式（点值表达式）。为什么能表示成这种方式呢？建议去翻一翻数学书。。。不过感性理解一下两点确定一条直线，三点确定一个二次函数。所以 n+1 n + 1 个点好像也可以反推一个 n n 次多项式。

然后是不是有一个很直观的想法：把这两个多项式分别变成点值表达式，然后把两个点乘起来，会得到答案的一个点值。现在如果我们有答案的次数+1个点，是不是就可以反推这个多项式呢？

举个例子：

1+x1——(0,1)(1,2)(2,3) 1 + x 1 — — ( 0 , 1 ) ( 1 , 2 ) ( 2 , 3 )

1+2∗x1——(0,1)(1,3)(2,5) 1 + 2 ∗ x 1 — — ( 0 , 1 ) ( 1 , 3 ) ( 2 , 5 )

然后我们就得到了 (0,1)(1,6)(2,15)——2∗x2+3∗x1+1 ( 0 , 1 ) ( 1 , 6 ) ( 2 , 15 ) — — 2 ∗ x 2 + 3 ∗ x 1 + 1

可以手动验证一波，不过肯定是对的。

现在的问题在于：我们如何把一个多项式迅速变成点值表达式，还有把一个点值表达式变成一个多项式。FFT就发挥了它的作用，想想我们带入的特殊值对吧，它现在没有什么性质。如果我们把它变得更有性质一些，是不是可以把程序变得更快呢？答案是当然的！

我们引入一个概念：复平面。

复平面就是可以把一个复数点变成一个向量

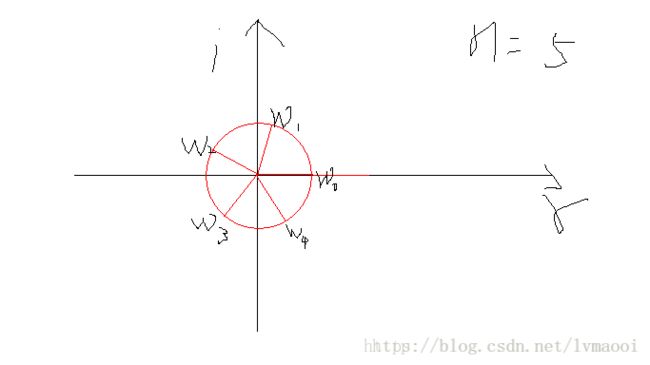
然后我们再学习单位根。型如 xn=1 x n = 1 在复数域内的所有根称为 x x 的 n n 次单位根

举个例子： n=2时（1，−1） n = 2 时 （ 1 ， − 1 ） ； n=4 n = 4 时 （1，−1，i，−i） （ 1 ， − 1 ， i ， − i ）

根据单位根的性质， n n 次单位正好把复平面分成 n n 份（至于为什么我也不知道），而且单位根嘛，向量长度为1

画个图理解一下：

然后在说单位根的几个性质（我也不知道为什么）

也就是说 w w 的下标和指数是可以随意转换的。

于是我们想到一种递归的做法（函数返回一个数组， x[i] x [ i ] 表示把 w[i] w [ i ] 带入式子的值：

void fft(E *x,int n,int type)  
{  
    if(n==1) return;  
    E l[n>>1],r[n>>1];  
    for(int i=0;i2)  
      l[i>>1]=x[i],r[i>>1]=x[i+1];  
    fft(l,n>>1,type);fft(r,n>>1,type);  
    E wn(cos(2*py/n),sin(type*2*py/n)),w(1,0),t;  
    for(int i=0;i>1;i++,w=w*wn)  
      t=w*r[i],x[i]=l[i]+t,x[i+(n>>1)]=l[i]-t;  
}  

我们来看一看，假设递归到了这一层(因为是平分成两段，所以下一层的w[i]是这一层的 w[2i] w [ 2 i ] ， wn w n 是 n n 次下的1次单位根，实际等于 w[1] w [ 1 ] )
然后推一波式子（假设长度为8）： l[i]=a0+a2∗w[2i]+a4∗w[4i]+a6∗w[6i] l [ i ] = a 0 + a 2 ∗ w [ 2 i ] + a 4 ∗ w [ 4 i ] + a 6 ∗ w [ 6 i ] ;
r[i]=a1+a3∗w[2i]+a5∗w[4i]+a7∗w[6i] r [ i ] = a 1 + a 3 ∗ w [ 2 i ] + a 5 ∗ w [ 4 i ] + a 7 ∗ w [ 6 i ] ;

l[i]=a0+a2∗w2i+a4∗w4i+a6∗w6i l [ i ] = a 0 + a 2 ∗ w i 2 + a 4 ∗ w i 4 + a 6 ∗ w i 6 ;
r[i]=a1+a3∗w2i+a5∗w4i+a7∗w6i r [ i ] = a 1 + a 3 ∗ w i 2 + a 5 ∗ w i 4 + a 7 ∗ w i 6 ;

由于 w w 在循环里所以 w=w[1]i=wi w = w [ 1 ] i = w i

推出： t=a1∗w1i+a3∗w3i+a5∗w5i+a7∗w7i t = a 1 ∗ w i 1 + a 3 ∗ w i 3 + a 5 ∗ w i 5 + a 7 ∗ w i 7 ;

所以当前： x[i]=l[i]+t x [ i ] = l [ i ] + t ;

然后为什么 x[i+(n>>1)]=l[i]−t x [ i + ( n >> 1 ) ] = l [ i ] − t ;

假设 A(wi)=Al(wi)+Ar(wi)∗w1 A ( w i ) = A l ( w i ) + A r ( w i ) ∗ w 1 ;所以 A(wi+n2)=Al(wi+n2)+Ar(wi+n2∗w1) A ( w i + n 2 ) = A l ( w i + n 2 ) + A r ( w i + n 2 ∗ w 1 ) ;由于Al里全是平方，不取负，Ar里全是奇数次方，所以取负。

然后如何把点值表达式再变成多项式表达。这个我是真不咋会。大概是这样的，我们做一遍FFT大概就是做了一个矩阵乘法，然后我们求它的逆矩阵。经证明可得把所有 wi w i 变为 w−i w − i 然后在除一个 n n 就是逆矩阵，所以可以看到上面的代码中type表示是逆向还是正向做FFT

我们现在学会FFT了然后去洛谷上交一波P3803 【模板】多项式乘法（FFT）

？？？嗯，怎么只有66分，我咋还re了，我咋还tle了。然后发现这个板子并不可用，真tm慢。我们可能还要学一波非递归版本。

由于我们只有在向下递归时才打乱数组顺序，所以我们不如先把数组位置排好，直接倍增向上。

位置怎么排呢？我们会发现一个很有趣的结论。在 0 0 ~ n n ( n n 是2的整次幂)的情况下， x x 的位置正好在 x x 在 2 2 进制 n n 位下取反。那我们先把位置排好岂不美哉。

来看看代码：

#include  
#include  
#include  
#include  
#include  
#define E complex  
#define py acos(-1)  
using namespace std;  

int n,m,x,L;  
E a[2624150],b[2624150];  
int p[2624150];//请不要在意这么魔性的数字，（好吧，去掉个零是2的某整次幂，hzwer当时板子是1e5的，结果这道题变1e6了）  

void fft(E *g,int type)  
{  
    for(int i=0;i//把位置排好，注意这个判断，要是没有判断的话就交换两次换回去了。就只用交换小的或者大的。  
      if(ifor(int i=1;i1)//枚举小段长度  
    {  
        E wn(cos(py/i),type*sin(py/i));注意这里的py不乘2，因为我们把两个小段合成大段，所以wn应该是大段长度的单位根。而上面递归版本要乘2，因为它的段长正好是大段。总之就是2*py/i中的i一定是合并后的大段长度  
        for(int j=0;j2*i)//枚举每一大段  
        {  
            E w(1,0);  
            for(int k=j;k//枚举第一小段内的每一个元素  
            {  
                E x=g[k],y=g[k+i]*w;  
                g[k]=x+y;g[k+i]=x-y;第一小段是+，第二小段是-。  
            }  
        }  
    }  
}  

int main()  
{  
    scanf("%d%d",&n,&m);  
    for(int i=0,x;i<=n;i++) scanf("%d",&x),a[i]=x;  
    for(int i=0,x;i<=m;i++) scanf("%d",&x),b[i]=x;  
    m=n+m;for(n=1;n<=m;n<<=1) L++;  
    for(int i=0;i>1]>>1)|((i&1)<<(L-1));//这一行比较精髓，就是说我们p[i>>1]取反数已经推出。我们在它的最前面插入i的最末位就好了  
    fft(a,1);fft(b,1);  
    for(int i=0;i<=n;i++) a[i]*=b[i];  
    fft(a,-1);  
    for(int i=0;i<=m;i++) printf("%d ",(int)(a[i].real()/n+0.5));  
}