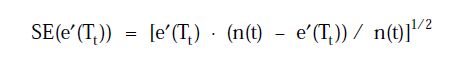决策树的剪枝操作
首先先介绍几个基本概念:
决策树(Decision Tree):在已知各种情况发生概率的基础上,通过构成决策树来求取净现值的期望值大于等于零的概率,评价项目风险,判断其可行性的决策分析方法,是直观运用概率分析的一种图解法。由于这种决策分支画成图形很像一棵树的枝干,故称决策树。
拟合:所谓拟合是指已知某函数的若干离散函数值{f1,f2,…,fn},通过调整该函数中若干待定系数f(λ1, λ2,…,λn),使得该函数与已知点集的差别(最小二乘意义)最小。
剪枝是指将一颗子树的子节点全部删掉,根节点作为叶子节点,以下图为例:
噪声数据:指在一组数据中无法解释的数据变动,就是一些不和其他数据相一致的数据。这些数据可能会干扰挖掘结果的质量,对于一些噪声敏感的挖掘算法,这些数据可能会导致挖掘结果出现大的偏差。
置信区间:设θ'在大样本下服从E(θ') = θ, 标准误差为σ'的正态分布,那么θ的(1 - α)100%置信区间是: θ' +/- (Zα/2) σ'
二项式概率分布:
均值和方差分别是u = np, σ2=npq ,其中p=每次实验成功的概率, q=1-p。
二项分布的正态逼近
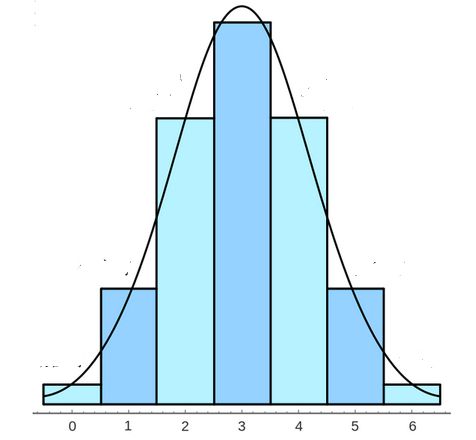
如果np>=4 且nq>=4 ,二项概率分布p(y)逼近于正态分布。如下图
可以看到P(Y<=2)是在正态曲线下Y=2.5的左端面积。注意到Y=2的左端面积是不合适的,因为它省略了相应于Y=2的一半概率的长方形。为了修正,用连续概率分布去近似离散概率分布,在计算概率之前我们需要将2增加0.5。值0.5称为二项概率分布近似的连续性修正因子,因此
P(Y<=a) 约等于 P(Z< (a+0.5 - np/ ( npq)1/2) );
P(Y>=a) 约等于 P(Z> (a-0.5 - np/ ( npq)1/2) )
既然都建成了决策树,为什么还要进行剪枝:
决策树是充分考虑了所有的数据点而生成的复杂树,有可能出现过拟合的情况,决策树越复杂,过拟合的程度会越高。(理论来说,不应该是拟合程度越高,预测结果越准确嘛?为什么还要避免这种情况?)
考虑极端的情况,如果我们令所有的叶子节点都只含有一个数据点,那么我们能够保证所有的训练数据都能准确分类,但是很有可能得到高的预测误差,原因是将训练数据中所有的噪声数据都”准确划分”了,强化了噪声数据的作用。(形成决策树的目的作出合理的预测,尽可能有效的排除噪声数据干扰,影响正确预测的判断)
剪枝修剪分裂前后分类误差相差不大的子树,能够降低决策树的复杂度,降低过拟合出现的概率。(换句话说就是把重负累赘的子树用一个根节点进行替换,也就是说跟姐的数据意义完全可以代替又该节点衍生出的子树的所有节点的意义)
既然决定剪枝,那么怎么进行剪枝呢?
两种方案:先剪枝和后剪枝
先剪枝说白了就是提前结束决策树的增长,跟上述决策树停止生长的方法一样。
后剪枝是指在决策树生长完成之后再进行剪枝的过程。这里介绍两种后剪枝方案:
方案一:REP—错误消减剪枝
错误消减剪枝是对“基于成本复杂度的剪枝”的一种优化,但是仍然需要一个单独的测试数据集,不同的是在于这种方法可以直接使用完全诱导树对测试集中的实例进行分类,对于诱导树(什么是诱导树?)中的非叶子节树,该策略是用一个叶子节点去代替该子树,判断是否有益,如果剪枝前后,其错误率下降或者是不变,并且被剪掉的子树不包含具有相同性质的其他子树(为什么不能包含相同性质的其他子树?欢迎评论!),那么就用这个叶子节点代替这个叶子树,这个过程将一直持续进行,直至错误率出现上升的现象。
简单点说:该剪枝方法是根据错误率进行剪枝,如果一棵子树修剪前后错误率没有下降,就可以认为该子树是可以修剪的。REP剪枝需要用新的数据集,原因是如果用旧的数据集,不可能出现分裂后的错误率比分裂前错误率要高的情况。由于使用新的数据集没有参与决策树的构建,能够降低训练数据的影响,降低过拟合的程度,提高预测的准确率。
方案二:PEP-悲观剪枝法(这一部分摘自http://www.cnblogs.com/junyuhuang/p/4572408.html,不属于原创理论)
不需要单独的数据集进行测试,而是通过训练数据集上的额错误分类数量来估算位置实力上的错误率。
PEP后剪枝技术是由大师Quinlan提出的。它不需要像REP(错误率降低修剪)样,需要用部分样本作为测试数据,而是完全使用训练数据来生成决策树,又用这些训练数据来完成剪枝。 决策树生成和剪枝都使用训练集, 所以会产生错分。现在我们先来介绍几个定义。
T1为决策树T的所有内部节点(非叶子节点),
T2为决策树T的所有叶子节点,
T3为T的所有节点,有T3=T1∪T2,
n(t)为t的所有样本数,
ni(t)为t中类别i的所有样本数,
e(t)为t中不属于节点t所标识类别的样本数
在剪枝时,我们使用
r(t)=e(t)/n(t)
就是当节点被剪枝后在训练集上的错误率,而
在此,我们把错误分布看成是二项式分布,由上面“二项分布的正态逼近”相关介绍知道,上面的式子是有偏差的,因此需要连续性修正因子来矫正数据,有
r‘(t)=[e(t) + 1/2]/n(t)
和
 , 其中s为t节点的叶子节点,你不认识的那个符号为 t的所有叶子节点的数目
, 其中s为t节点的叶子节点,你不认识的那个符号为 t的所有叶子节点的数目
为了简单,我们就只使用错误数目而不是错误率了,如下
e'(t) = [e(t) + 1/2]
接着求e'(Tt)的标准差,由于误差近似看成是二项式分布,根据u = np, σ2=npq可以得到
当节点t满足
则Tt就会被裁减掉。