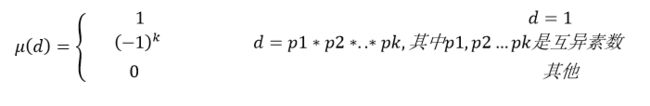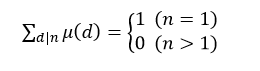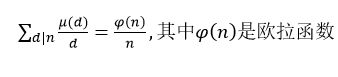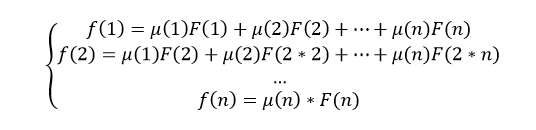莫比乌斯反演学习笔记

莫比乌斯反演的形式：

另一种描述是：

一种是和所有的约数有关一种是和所有的倍数有关，解题的时候要根据题目选择合适的表达形式，感觉第二种用的比较多。

关于莫比乌斯函数mu，他的定义如下：

这个莫比乌斯函数有一些性质：

（1）

（2）

一般需要预处理所有的莫比乌斯函数值，需要用到线性筛

mu[1] = 1;
for (int i = 2; i <= maxn; i++) {
    if (!vis[i]) {
        prime[cnt++] = i;
        mu[i] = -1;
    }
    for (int j = 0; j < cnt; j++) {
        if (i*prime[j] > maxn)
            break;
        vis[i*prime[j]] = 1;
        if (i%prime[j] == 0) {
            mu[i*prime[j]] = 0;
            break;
        }
        else {
            mu[i*prime[j]] = -mu[i];
        }
    }
}

做了几道基础的莫比乌斯反演题目来加深一下

HDU1695：点击打开链接

题意是[1,n],[1,m]两个区间中有多少对数的gcd是k。

先把题目转化为[1,n/k],[1,m/k]两个区间中有多少对数互质，可以用容斥原理求出所有gcd不为1的对数求出结果，但是用莫比乌斯反演可以更加高效的求解。

假设f(x)表示gcd为x的对数，F(x)表示gcd为x倍数的对数，那么显然f(x)和F(x)满足莫比乌斯反演的第二种描述，我们需要求出f(1):

f(1)=mu(1)F(1)+mu(2)F(2)+mu(3)F(3)+....，显然对于区间[1,a],[1,b]有F(x)=(a/x)*(b/x),所以到x=min(a,b)之后就不需要累计了因为F(x)始终为0。

然后因为题目规定了(a,b)和(b,a)算成一种，所以最终结果需要处理一下。

#include 
#include 
#include 
#include 
using namespace std;
#define maxn 111111

long long a, b, c, d, k;
long long prime[maxn], cnt;
bool vis[maxn];
int mu[maxn];

void get_mu () {
    cnt = 0;
    memset (vis, 0, sizeof vis);
    mu[1] = 1;
    for (long long i = 2; i <= 100000; i++) {
        if (!vis[i]) {
            prime[cnt++] = i;
            mu[i] = -1;
        }
        for (long long j = 0; j < cnt; j++) {
            if (i*prime[j] > 100000)
                break;
            vis[i*prime[j]] = 1;
            if (i%prime[j] == 0) {
                mu[i*prime[j]] = 0;
                break;
            }
            else {
                mu[i*prime[j]] = -mu[i];
            }
        }
    }
}

long long solve (long long n, long long m) {
    long long ans = 0;
    for (long long i = 1; i <= n; i++) {
        ans += mu[i]*((long long)(n/i) * (long long)(m/i));
    }
    return ans;
}

int main () {
    //freopen ("in.txt", "r", stdin);
    get_mu ();
    int t, kase = 0;
    scanf ("%d", &t);
    while (t--) {
        scanf ("%lld%lld%lld%lld%lld", &a, &b, &c, &d, &k);
        if (k == 0) {
            printf ("Case %d: 0\n", ++kase);
            continue;
        }
        b /= k; d /= k;
        if (b > d)
            swap (b, d);
        printf ("Case %d: %lld\n", ++kase, solve (b, d)-solve (b, b)/2);
    }
    return 0;
}

BZOJ2301：点击打开链接

和上面那题很类似。

假设经过处理上下界以后是求出[a,b],[c,d]的互质对数，如果ans(x,y)表示[1,x],[1,y]的互质对数，那么根据容斥原理，也就是求出ans(b,d)+ans(a-1,c-1)-ans(a-1,d)-ans(c-1,b)。

但是数据组数很多如果继续使用遍历复杂度将会达到O(q*n)显然会爆炸，可以使用分块加速思想。

也就是需要Σ[n/i]中间结果会有很多相同的数，可以发现[i,n/(n/i)]之间的结果是相等的，也就是F(i)到

F(min(n/(n/i), m/(m/i)))之间的结果是相同的，所以可以先预处理mu函数的前缀和。复杂度变成了O(q*sqrt (n))。

#include 
#include 
#include 
#include 
#include 
using namespace std;
#define maxn 51111

long long a, b, c, d, k;
long long prime[maxn], cnt;
bool vis[maxn];
int mu[maxn];
long long sum[maxn];

void get_mu () {
    memset (vis, 0, sizeof vis);
    cnt = 0;
    mu[1] = 1;
    for (int i = 2; i <= 50000; i++) {
        if (!vis[i]) {
            prime[cnt++] = i;
            mu[i] = -1;
        }
        for (int j = 0; j < cnt; j++) {
            if (i*prime[j] > 50000)
                break;
            vis[i*prime[j]] = 1;
            if (i%prime[j] == 0) {
                mu[i*prime[j]] = 0;
                break;
            }
            else {
                mu[i*prime[j]] = -mu[i];
            }
        }
    }

    sum[0] = 0;
    for (int i = 1; i <= 50000; i++)
        sum[i] = sum[i-1]+mu[i];
}

long long solve (long long a, long long b) {
    long long ans = 0;
    if (a > b)
        swap (a, b);
    long long j;
    for (long long i = 1; i <= a; i = j+1) {
        j = min (a/(a/i), b/(b/i));
        ans += (sum[j]-sum[i-1])*(long long)(a/i)*(long long)(b/i);
    }
    return ans;
}

int main () {
    get_mu ();
    int t;
    scanf ("%d", &t);
    while (t--) {
        scanf ("%lld%lld%lld%lld%lld", &a, &b, &c, &d, &k);
        b /= k, d /= k;
        a = ceil (a*1.0/k), c = ceil (c*1.0/k);
        printf ("%lld\n", solve (b, d) + solve (a-1, c-1) - solve (a-1, d) - solve (c-1, b));
    }
    return 0;
}

HDU4746：点击打开链接

题意：在区间[1,a][1,b]中有多少对数的gcd满足：他们的gcd分解后素因子数小于等于p。

同样的假设f(x)表示gcd为x的对数，F(x)表示gcd为x倍数的对数，可以有：

于是就可以对于每一个i，求出这个i在自己的质因子数下对F(x)的贡献，然后通过前缀和和分块加速，和上题类似的做法就可以在O(q*sqrt(n))时间内求出结果。

#include 
#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;
#define maxn 511111

vector  fac[maxn];
int prime[maxn], cnt;
bool vis[maxn];
int mu[maxn];
int num[maxn]; //每个数能够分解成几个质数
long long sum[maxn][22];
long long n, m;int p;

void init () {
    memset (vis, 0, sizeof vis);
    for (int i = 1; i <= 500000; i++)
        fac[i].clear ();
    cnt = 0;
    mu[1] = 1;
    for (int i = 2; i <= 500000; i++) {
        if (!vis[i]) {
            prime[cnt++] = i;
            mu[i] = -1;
        }
        for (int j = 0; j < cnt; j++) {
            if (i*prime[j] > 500000)
                break;
            vis[i*prime[j]] = 1;
            if (i%prime[j] == 0) {
                mu[i*prime[j]] = 0;
                break;
            }
            else {
                mu[i*prime[j]] = -mu[i];
            }
        }
    }

    memset (vis, 0, sizeof vis);
    memset (num, 0, sizeof num);
    num[1] = 0;
    for (int i = 2; i <= 500000; i++) {
        if (!vis[i]) {
            for (int j = i; j <= 500000; j += i) {
                vis[j] = 1;
                int cur = j;
                while (cur%i == 0) {
                    cur /= i;
                    num[j]++;
                }
            }
        }
    } 

    memset (sum, 0, sizeof sum);
    for (int i = 1; i <= 500000; i++) {
        for (int j = i; j <= 500000; j += i) {
            sum[j][num[i]] += mu[j/i];
        }
    }
    for (int i = 1; i <= 500000; i++) {
        for (int j = 0; j <= 18; j++) {
            sum[i][j] += sum[i-1][j];
        }
    }
    for (int i = 1; i <= 500000; i++) {
        for (int j = 1; j <= 18; j++) {
            sum[i][j] += sum[i][j-1];
        }
    }
}

int main () {
    init ();
    int q;
    scanf ("%d", &q);
    while (q--) {
        scanf ("%lld%lld%d", &n, &m, &p);
        if (p >= 19) {
            printf ("%lld\n", n*m);
            continue;
        }
        p = min (18, p);
        long long ans = 0;
        int j;
        for (int i = 1; i <= min (n, m); i = j+1) {
            j = min (n/(n/i), m/(m/i));
            ans += (long long)(sum[j][p]-sum[i-1][p])*(long long)(n/i)*(long long)(m/i);
        }
        printf ("%lld\n", ans);
    }
    return 0;
}