机器学习——线性回归

线性回归

线性回归，就是通过给定的数据学习得到一个线性模型以尽可能准确的预测实值的输出。
基本形式：
$f(x)=w_1{x}_1+w_2{x}_2+\cdot \cdot \cdot +w_n{x}_n+b$
一般用向量表示：
$f(x)=W^{T}X+B$ 其中$W和B$ 是待学习的参数。
一个简单的例子：

#import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
# y = wx +b

# 计算误差
def compute_error(b,w,data):
    total_error = 0
    for i in range(0, len(points)):
        x = points[i, 0]
        y = points[i, 1]
        total_error += (y - (w*x + b)) ** 2
    return total_error/float(len(points))

def step_gradient(param_b,param_w,points,lr):
    b_gradient = 0
    w_gradient = 0
    N = float(len(points))
    for i in range(0, len(points)):
        x_c = points[i, 0]
        y_c = points[i, 1]
        b_gradient += (2/N) * ((param_w * x_c + param_b) - y_c)
        w_gradient += (2/N) * x_c * ((param_w * x_c + param_b) - y_c)
    new_b = param_b - lr * b_gradient
    new_w = param_w - lr * w_gradient
    return new_b, new_w


def gradient_descent(points, param_b, param_w, lr, iter_num):
    b_c = param_b
    w_c = param_w
    for i in range(iter_num):
        b_c, w_c = step_gradient(b_c, w_c, np.array(points), lr)
    return b_c, w_c



if __name__ == '__main__':
    points = np.genfromtxt("data.csv", delimiter=",")
    x = points[:, 0]
    y = points[:, 1]
    fig = plt.figure()
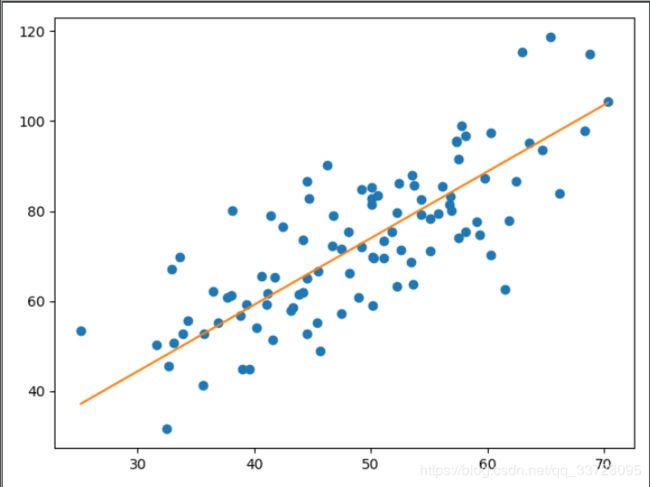
    plt.plot(x, y, 'o')  # 数据可视化
    # plt.show()
    #
    lr = 0.0001
    param_b = 0
    param_w = 0
    iter_num = 1000
    print(compute_error(param_b, param_w, points))

    b, w = gradient_descent(points, param_b, param_w, lr, iter_num)
    print(w, b, compute_error(b, w, points))
    x_end = max(points[:, 0])
    x_begin = min(points[:, 0])
    y_begin = w * x_begin + b
    y_end = w * x_end + b
    plt.plot((x_begin, x_end), (y_begin, y_end))
    plt.show()