【Deep Learning】M2Det: A Single-Shot Object Detector based on Multi-Level Feature Pyramid Network解读

1. M2Det 论文思维导图

  该思维导图使用 MindMaster 软件做出，源文件可以点击链接进行下载。

2. Abstract

  在目标检测网络中应用特征金字塔结构在目标检测网络中已经成为一种趋势，如单阶段目标检测中的的 DSSD，RetinaNet，RefineDet，还有双阶段目标检测中的 Mask R-CNN, DetNet 等结构。通过应用特征金字塔，这些网络在解决目标多尺度问题上有了一定的进步。但由于上述网络中的这些特征金字塔结构最初设计是用于目标分类任务的结构，因此在目标检测任务上他们具有一定的局限性。在本文中，作者提出了多层特征金字塔网络（MLFPN）来构建更有效的特征金字塔结构，以此用于检测不同尺度的目标。

1. 首先融合骨干网提出的多级特征作为基础特征
2. 把基本的特征加入一组交替连接的u型模块和特征融合模块，利用每个u型模块的解码器层作为目标检测的特征
3. 将具有等效尺度(大小)的解码器层集合起来，形成一个用于目标检测的特征金字塔，其中每个特征图由多个层次的层(特征)组成

  为了充分利用上述的 MLFPN 结构，将其应用在 SSD 结构中并设计了一种出色的端到端的单阶段目标检测器，即 M2Det。最终在 COCO 数据集上，单尺度检测达到了fps 为11.8，且 AP 为41.0。在多尺度检测上，AP 为 44.2。这个结果是目前单阶段目标检测网络所能达到的最好的水平

3. Introduction

  目标的多尺度特性是设计目标检测网络的一个主要挑战，当前通常有两种方法用来解决这个问题。即：

• 在测试阶段使用图像金字塔（Cascade RCNN）
• 从输入图像提取出的特征金字塔上进行检测

上述第一种方法是将原始图像进行一系列的缩放，因此会增加计算开销，从而使得目标检测网络的整体效率发生很严重的下降。第二种方法直接使用卷积神经网络中的不同特征层，因此可以同时应用于训练和测试阶段中，相对来讲开销较小，易于进行集成，比较容易做到 end-to-end。

  由于利用特征金字塔本身是为目标分类任务设计的，因此直接应用到目标检测时会存在一定的缺陷，论文中给出了四种不同的利用特征金字塔的结构：

图中的四种结构分别为：SSD 型，FPN 型，STDN 型和本文所使用的 MLFPN 型。前三种的缺点主要有两点：

• 都是基于分类网络作为base net 的特征提取结构
• 每个 feature map 仅由 base net 的一个尺度(single level)的特征给出

对于第二点，论文中也进行了相关说明，即通常来讲，卷积神经网络中的高层特征利于分类任务的进行，而低层特征则利于回归目标的位置。

• SSD-style: 利用了base net 中的最后两层以及额外添加的一系列的 strides=2 的特征层作为输出特征
• FPN-style：通过对每个特征层进行与尺度相同的上采样操作得到的特征层进行融合，从而获取到多尺度的特征
• STDN-style: 利用 DenseNet 的最后一个 dense block，并结合 池化和 scale-transfer 操作来构建特征金字塔
• MLFPN-style：Multi-level&Multi-scale

这篇文章的目的是构筑一个更加有效的特征金字塔对不同尺度的目标进行检测：

• 首先把从骨干网提取的多层特征融合起来作为基本的特征，然后把它加入交替连接的TUM和FFM来提取更多表示，多层多尺度特征。值得注意的是，每个 u 型模块中的解码器层具有相似的深度。
• 将具有等效尺度的特征映射集合起来，构建最终的特征金字塔进行目标检测。显然，构成最终特征金字塔的解码器层要比主干层深得多，即更具代表性。
• 在最终的特征金字塔中，每个特征映射都由多个层次的解码器层组成。因此，我们称我们的特征金字塔块为多层次特征金字塔网络(MLFPN)。

4. Proposed Method

  基于此，本文提出了一种 MLFPN 的结构，该结构的整体图如下所示：

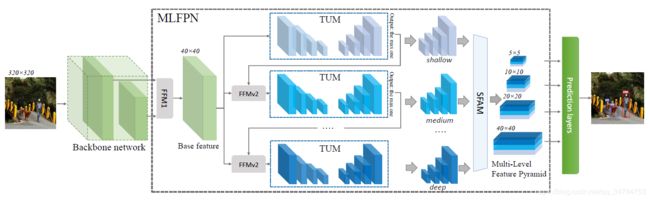
  上图的大致流程为：

• 对主干网络提取到的特征进行融合操作；
• 通过 TUM 和 FFM 操作提取出更有代表性的 Multi-level & Multi-scale 的特征
• 通过 SFAM 融合多级特征
• 得到 多级特征金字塔用于最后的目标检测。

  而 M2Det 目标检测结构就是基于上图的，它使用骨干网络和 MLFPN 从输入图像中提取特征，然后进行类似 SSD 的操作，在学习到的特征上产生密集的 bounding boxes 和分类得分，然后使用 NMS 操作来产生最终的结果。

  从上图中可以看出，MLFPN 主要的操作有 3 个，即 FFM(v1&v2)，TUM 和 SFAM。首先，利用 FFMv1 融合浅层和深层特征，形成基础特征，如 VGG 中的 conv4_3 和 conv5_3，从而为 MLFPN 提供更多的尺度的语义信息。然后采用几个 TUM 和 FFMv2 进行交替堆叠。其中每个 TUM 都会生成几个不同尺度的 feature map。

  FFMv2 将 base net 的特征与前一个 TUM 输出的最大的特征图进行融合。融合得到的特征图被送入到下一个 TUM 模块中，但是第一个 TUM 并没有进行融合操作，也就是他的输入仅由 base net 的特征组成。即 $X_{base}$。最终输出的多尺度特征的计算方式如下：
$$[x_1^l,x_2^l,...,x_i^l]=\{\begin{array}{rc}{\mathbf{T}}_l({\mathbf{X}}_{base}),& l=1\\ {\mathbf{T}}_l(\mathbf{F}({\mathbf{X}}_{base},x_i^{l-1})),& l=2,...,L\end{array}$$
其中，${\mathbf{X}}_{base}$ 指的是 backbone 得到的特征图，$x_i^l$ 指的是在第 $l$ 个 TUM 中的第 $i$ 个 $scale$ 的特征，$L$ 指的是 TUM 的数量，${\mathbf{T}}_l$ 指的是第 $l$ 个 TUM 模块，$\mathbf{F}$ 指的是 FFMv1 操作。

  最后，SFAM 模块通过 scale-wise 的拼接以及 channel-wise attention 来对 multi-level 和 multi-scale 的特征进行聚合并使用。

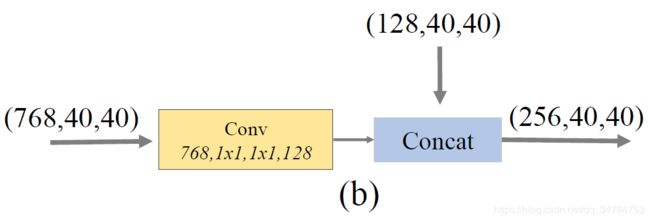
4.1 FFMs

   FFMs 用于融合 M2Det 中不同级别的特征，首先通过 $1\times 1$ 卷积来对特征图的通道进行压缩，然后再进行通道方向上的拼接操作。具体来说：

• FFMv1：使用两种不同尺度的特征图作为输入，因此在进行 concatenation 操作前需要进行上采样操作。

  具体如下图所示：
  

• FFMv2：使用 base feature 和上一个 TUM 输出中最大的特征图进行拼接，因为尺度相同，因此不需要进行上采样操作。具体如下如所示：
  

4.2 TUMs

  TUM 模块使用了与 FPN 和 RetinaNet 相比更为轻薄的 U 形网络。它的编码器部分为一系列 strides=2 的 $3\times 3$ 的卷积层。而解码器讲这些层的输出作为其特征映射的参考集，原始的 FPN 选择 ResNet 主体网络中每个阶段的最后一层的输出。另外，在解码器分支上进行上采样和 element-wise 求和运算后使用 $1\times 1$ 卷积操作来提升学习能力以及保持特征的平滑度（smoothness）。TUM 中每一个转义码的输出都形成了当前层的多尺度特征。总体而言，堆积 TUMs 的输出形成了多层次，多尺度的特征。因此前面的 TUM 主要是用来提供浅层的特征，中间的 TUM 主要提供中层特征，后面的 TUM 主要提供深层特征。具体如下图所示：

4.3 SFAM

  SFAM 的作用是将上一结构 TUMs 生成的多级尺度特征集合成为一个多级特征金字塔。具体结构如下图所示：

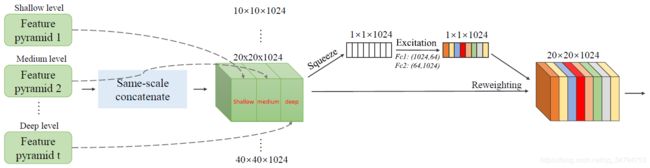
  SFAM 中第一阶段是沿着通道方向将相同尺度的特征度拼接起来，即使用 concatenation 操作来完成，聚合后的特征金字塔可以表示为 $\mathbf{X}=[{\mathbf{X}}_1,{\mathbf{X}}_2,...,{\mathbf{X}}_i]$，其中，${\mathbf{X}}_i,=Concat({\mathbf{x}}_i^1,{\mathbf{x}}_i^2,...,{\mathbf{x}}_i^L)\in {\mathbb{R}}^{W_i\times H_i\times C}$是第 $i$ 大尺度的特征。在这里，聚合金字塔中的每个尺度都包含来自于多层深度的特征。然而，简单的连接操作并不能有足够的自适应性。

  因此，SFAM 中第二阶段引入了一个面向通道的注意力模块， 通过这种机制来鼓励特征图集中在它们受益最大的通道上。根据 SE block 中的操作，我们在 squeeze 阶段使用 GAP（全局平均池化）操作来得到具有全局特征的通道统计特征$\mathbf{z}\in {\mathbb{R}}^C$ ，在接下来的 Excitation 阶段通过下面的注意力机制来进行学习：
$$\mathbf{s}={\mathbf{F}}_{ex}(\mathbf{z},\mathbf{W})=\sigma ({\mathbf{W}}_2\delta ({\mathbf{W}}_1\mathbf{z}))$$
上式中 $\sigma$ 表示 ReLU 激活函数，$\delta$ 表示 Sigmoid 激活函数，其中 ${\mathbf{W}}_1\in {\mathbb{R}}^{\frac{C}{r}\times C}，{\mathbf{W}}_2\in {\mathbb{R}}^{C\times \frac{C}{r}}$，$r=16$ 为压缩系数，最终的输出通过下面的公式得到：
$${\tilde{\mathbf{x}}}_c={\mathbf{F}}_{scale}({\mathbf{u}}_c,s_c)=s_c\cdot {\mathbf{u}}_c$$
$\tilde{\mathbf{X}}=[{\tilde{\mathbf{x}}}_1,{\tilde{\mathbf{x}}}_2,...,{\tilde{\mathbf{x}}}_C]$，其中每个都经过 ${\mathbf{s}}_c$ 进行加强或减弱处理。针对 SE block 更具体的介绍可以参考上一篇博客。

5.Network Configurations

  论文中采用两种类型的 backbone 网络来对 M2Det 进行构建。在训练整个网络之前，需要再 ImageNet 2012 数据集上对 backbone 网络进行与训练处理。MLFPN 默认情况下包含 8 个 TUM 模块，每个 TUM 有 5 个 striding-conv 和 5 个 upsampling 操作，因此最终将输出 6 个 scale 的特征。为了减少参数量，每 TUM 中每个尺度仅含有 256 个 channels，这样设置后网络能够轻松地在 GPU 上进行训练。对于输入图像的大小，采用原 SSD，RefineDet和 RetinaNet 中的数值，即 320,512 和 800。

  在检测阶段，作者在 6 个金字塔特征中分别加入 2 个卷积层来分别实现定位回归和分类。 6 个 feature map 默认框的检测尺度范围按照原始 SSD 进行设置。当输入图像大小为 800$\times$800 时，相应的特征图尺度从最小逐渐增长到最大尺度。在金字塔特征图中的每个像素点，都设置3个比率的共 6 个 anchors。然后，使用 0.05 来作为每个 anchors 的置信度得分的阈值。然后利用线性核的 soft-nms 进行处理，从而得到最终的回归框。 将上述阈值降低到 0.01 能够得到更好的检测效果，但是会增加网络的推理时间，因此最终并没有采用这 0.01 作为阈值。

6. 本文参考内容

1. M2Det: A Single-Shot Object Detector based on Multi-Level Feature Pyramid Network
2. 论文学习笔记-M2Det
3. M2Det: A Single-Shot Object Detector based on Multi-Level Feature Pyramid Network(论文解读)