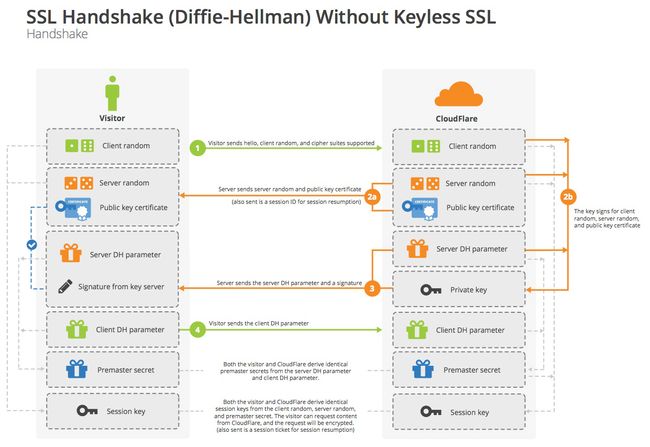
可参考此文章帮助理解:图解SSL/TLS协议(阮一峰)
1. DEA (Data Encryption Algorithm,即 数据加密算法)
常用加密算法为:AES 、 RSA/ECC 、Diffie-hellman 、 SHA-1/SHA-256(数据验证与指纹) 。
2. 对称加密算法
1. DES (DES全称为Data Encryption Standard,即数据加密标准)
是一种使用密钥加密的块算法,1976年被美国联邦政府的国家标准局确定为联邦资料处理标准(FIPS),随后在国际上广泛流传开来。
单密钥算法,是信息的发送方采用密钥A进行数据加密,信息的接收方采用同一个密钥A进行数据解密.
缺点:由于采用同一个密钥进行加密解密,在多用户的情况下,密钥保管的安全性是一个问题.
2. AES (Advanced Encryption Standard,即 高级加密标准),又称Rijndael加密法
严格地说,AES和Rijndael加密法并不完全一样(虽然在实际应用中二者可以互换),因为Rijndael加密法可以支持更大范围的区块和密钥长度:AES的区块长度固定为128 比特,密钥长度则可以是128,192或256比特;而Rijndael使用的密钥和区块长度可以是32位的整数倍,以128位为下限,256比特为上限。加密过程中使用的密钥是由Rijndael密钥生成方案产生。
AES是美国国家标准技术研究所NIST旨在取代DES的21世纪的加密标准。
AES_128_GCM 更安全
AES_128_CBC
…
3. 非对称加密算法
1. RSA 非对称加密
RSA公钥加密算法是1977年由罗纳德·李维斯特(Ron Rivest)、阿迪·萨莫尔(Adi Shamir)和伦纳德·阿德曼(Leonard Adleman)一起提出的。1987年首次公布,当时他们三人都在麻省理工学院工作。RSA就是他们三人姓氏开头字母拼在一起组成的。
RSA是目前最有影响力的公钥加密算法,它能够抵抗到目前为止已知的绝大多数密码攻击,已被ISO推荐为公钥数据加密标准。
RSA的安全性是基于极其困难的大整数的分解(两个素数的乘积)
2. DSA
基于整数有限域离散对数难题
一般用于数字签名和认证
在DSA数字签名和认证中,发送者使用自己的私钥对文件或消息进行签名,接受者收到消息后使用发送者的公钥
来验证签名的真实性。
DSA只是一种算法,和RSA不同之处在于它不能用作加密和解密,也不能进行密钥交换,
只用于签名,它比RSA要快很多.
3. ECC
RSA 与 DSA 各有优缺点,那有没一个更好的选择呢?答案是肯定的,ECC(Elliptic Curves Cryptography)
基于椭圆曲线算法。
ECC 与 RSA 相比,有以下的优点:
相同密钥长度下,安全性能更高,如160位ECC已经与1024位RSA、DSA有相同的安全强度。
计算量小,处理速度快,在私钥的处理速度上(解密和签名),ECC远 比RSA、DSA快得多。
存储空间占用小 ECC的密钥尺寸和系统参数与RSA、DSA相比要小得多, 所以占用的存储空间小得多。
带宽要求低使得ECC具有广泛得应用前景。
这使得ECC 取代RSA成为可能。(不知道谁说的)
4. Diffie-Hellman
Diffie-Hellman:一种确保共享KEY安全穿越不安全网络的方法,它是OAKLEY的一个组成部分。Whitefield与Martin Hellman在1976年提出了一个奇妙的密钥交换协议,称为Diffie-Hellman密钥交换协议/算法(Diffie-Hellman Key Exchange/Agreement Algorithm).这个机制的巧妙在于需要安全通信的双方可以用这个方法确定对称密钥。然后可以用这个密钥进行加密和解密。但是注意,这个密钥交换协议/算法只能用于密钥的交换,而不能进行消息的加密和解密。双方确定要用的密钥后,要使用其他对称密钥操作加密算法实际加密和解密消息。
DH 算法的握手阶段
整个握手阶段都不加密(也没法加密),都是明文的。因此,如果有人窃听通信,他可以知道双方选择的加密方法,以及三个随机数中的两个。整个通话的安全,只取决于第三个随机数(Premaster secret)能不能被破解。
虽然理论上,只要服务器的公钥足够长(比如2048位),那么Premaster secret可以保证不被破解。但是为了足够安全,我们可以考虑把握手阶段的算法从默认的RSA算法,改为 Diffie-Hellman算法(简称DH算法)。
采用DH算法后,Premaster secret不需要传递,双方只要交换各自的参数,就可以算出这个随机数。
DH算法的一个简单描述:
1) A随机产生一个大整数a,然后计算Ka=ga mod n。(a需要保密)
2) B随机产生一个大整数b,然后计算Kb=gb mod n。(b需要保密)
3) A把Ka发送给B,B把Kb发送给A
4) A计算K=Kba mod n
5) B计算K=Kab mod n
由于Kba mod n= (gb mod n)a mod n= (ga mod n)b mod n,因此可以保证双方得到的K是相同的,K即是共享的密钥。
意思是说client与server端都有一个随机数是不会通过网络传输的。所以保证了安全。
4. 数据完整性验证 (MD5 | SHA-*)
MessageDigest是一个数据的数字指纹.即对一个任意长度的数据进行计算,产生一个唯一指纹号.
MessageDigest的特性:
两个不同的数据,难以生成相同的指纹号
对于指定的指纹号,难以逆向计算出原始数据
5. 实例
1. 使用OPENSSL 生成基于RSA 的非对称加密算法 的命令如下:
生成一个密钥(私钥)
[root@hunterfu ~]# openssl genrsa -out private.key 1024
注意: 需要注意的是这个文件包含了公钥和密钥两部分,也就是说这个文件即可用来加密也可以用来解密,后面的1024是生成
密钥的长度.
通过密钥文件private.key 提取公钥
[root@hunterfu ~]# openssl rsa -in private.key -pubout -out pub.key
使用公钥加密信息
[root@hunterfu ~]# echo -n “123456” | openssl rsautl -encrypt -inkey pub.key -pubin >encode.result
使用私钥解密信息
[root@hunterfu ~]#cat encode.result | openssl rsautl -decrypt -inkey private.key
123456
2. 使用OPENSSL 生成基于DSA 的非对称加密算法 的命令如下:
生成一个密钥(私钥)
[root@hunterfu ~]# openssl dsaparam -out dsaparam.pem 1024
[root@hunterfu ~]# openssl gendsa -out privkey.pem dsaparam.pem
生成公钥
[root@hunterfu ~]# openssl dsa -in privkey.pem -out pubkey.pem -pubout
[root@hunterfu ~]# rm -fr dsaparam.pem
使用私钥签名
[root@hunterfu ~]# echo -n “123456” | openssl dgst -dss1 -sign privkey.pem > sign.result
使用公钥验证
[root@hunterfu ~]# echo -n “123456” | openssl dgst -dss1 -verify pubkey.pem -signature sign.result