网易笔试题：整理房间

题目描述：
又到了周末，小易的房间乱得一团糟。
他希望将地上的杂物稍微整理下，使每团杂物看起来都紧凑一些，没有那么乱。
地上一共有n团杂物，每团杂物都包含4个物品。第i物品的坐标用(xi,yi)表示，小易每次都可以将它绕着(ai,bi)逆时针旋转90^ \circ90
∘
，这将消耗他的一次移动次数。如果一团杂物的4个点构成了一个面积不为0的正方形，我们说它是紧凑的。
因为小易很懒，所以他希望你帮助他计算一下每团杂物最少需要多少步移动能使它变得紧凑。
输入描述:
第一行一个数n(1 <= n <= 100)，表示杂物的团数。
接下来4n行，每4行表示一团杂物，每行4个数xi, yi，ai, bi, (-104 <= xi, yi, ai, bi <= 104)，表示第i个物品旋转的它本身的坐标和中心点坐标。
输出描述:
n行，每行1个数，表示最少移动次数。
示例1
4
1 1 0 0
-1 1 0 0
-1 1 0 0
1 -1 0 0
1 1 0 0
-2 1 0 0
-1 1 0 0
1 -1 0 0
1 1 0 0
-1 1 0 0
-1 1 0 0
-1 1 0 0
2 2 0 1
-1 0 0 -2
3 0 0 -2
-1 1 -2 0
输出
1
-1
3
3

  思路：这个题目是比较考察人的编程能力的，最简单的方法就是暴力枚举，依次把每个点旋转4次（旋转0次、1次、2次、3次），判断旋转之后的点是否构成正方形。
  这个题的难点有两个部分，一是旋转后的坐标的确定，二是判断给定任意四个点，它们是否能够成正方形。下面我将从这两个部分分别说明：

1.旋转后的坐标确定
  如图所示，可以按照这种方式来计算逆时针旋转后的点，设旋转前的点P坐标为（x,y）,旋转中心为（a,b），可以计算图中旋转前直角三角形的长边长为x-a,短边长为y-b,所以旋转后点的横坐标为a-(y-b)=a-y+b,同理可得纵坐标为x-a+b;所以旋转后的点的坐标为（a-y+b,x-a+b)。【如果x-a或y-b为负数，这个旋转后的坐标也是成立的，具体感兴趣的可以自己画个图算一下，这里不做赘述】

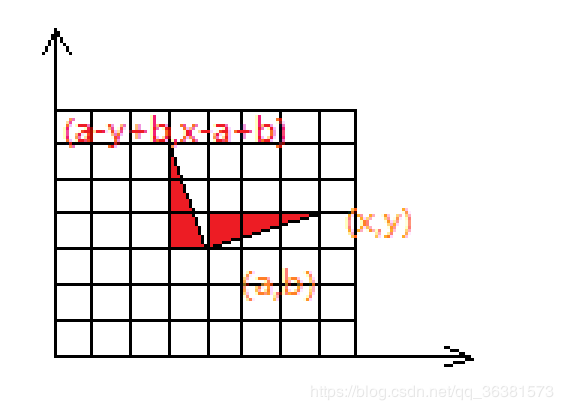
这部分的代码：

Point rotate(Point p, int times) {
	int x = p.x;
	int y = p.y;
	int a = p.a;
	int b = p.b;
	int xx, yy;
	for (int i = 0; i < times; i++) {
		xx = a - y + b;
		yy = x - a + b;
		x = xx;
		y = yy;
	}
	return Point(x, y, a, b);
}

.2.任意给定四个点，判断所给四个点是否为正方形
  回顾一下初中是怎么证明一个图形是正方形的吧。首先要证明这四条边都相等并且不为0，这说明这个四边形式菱形，然后再证明菱形中有一个是直角，即可证明这个四边形是正方形了。
  由于旋转后的四个点是无序的，为了证明方便，我们可以按照横坐标的大小升序排序，如果横坐标相同，则按纵坐标大小排序。我们声明升序排序后第一个坐标点为P0,第二个坐标点为P1,第三个坐标点为P2,第四个坐标点为P3,则要计算P0和P1,P0和P2,P1和P3,P2和P3之间的距离是相等的且不为0，然后再证明P0,P1,P2构成直角，即可证明这个四个点构成正方形。这部分的证明可以参考这篇博文。.
  这部分的代码：

bool cmp(Point p1, Point p2) {
	if (p1.x != p2.x) {//横坐标不相等按横坐标排序
		return p1.x < p2.x;
	}
	return p1.y < p2.y;//横坐标相等按纵坐标排序
}
bool isRightAngle(Point p1, Point p2, Point p3) {//判断是否为直角，按照向量相乘是否为0判断即可
	int x = (p1.x - p2.x)*(p1.x - p3.x) + (p1.y - p2.y)*(p1.y - p3.y);
	if (x == 0) {
		return true;
	}
	return false;
}
double distance(Point p1, Point p2) {//为了方便比较这里不做开方处理
	return (p1.x - p2.x)*(p1.x - p2.x) + (p1.y - p2.y)*(p1.y - p2.y);
}
bool isSquare(Point p1,Point p2,Point p3,Point p4) {//判断是否为正方形
	vector points(4);
	points[0] = p1;
	points[1] = p2;
	points[2] = p3;
	points[3] = p4;
	sort(points.begin(), points.end(), cmp);//升序排序
	int s1 = distance(points[0],points[1]);
	int s2 = distance(points[0], points[2]);
	int s3 = distance(points[1], points[3]);
	int s4 = distance(points[2], points[3]);
	if (s1 == s2 && s2 == s3 && s3 == s4 && s1 != 0 && isRightAngle(points[0], points[1], points[2])) {
		return true;
	}
	else {
		return false;
	}
	
}

3.整个AC代码：

#include
using namespace std;
struct Point {
	int x;
	int y;
	int a;
	int b;
	Point(int x, int y, int a, int b) {
		this->x = x;
		this->y = y;
		this->a = a;
		this->b = b;
	}
	Point() {}
};
Point rotate(Point p, int times) {
	int x = p.x;
	int y = p.y;
	int a = p.a;
	int b = p.b;
	int xx, yy;
	for (int i = 0; i < times; i++) {
		xx = a - y + b;
		yy = x - a + b;
		x = xx;
		y = yy;
	}
	return Point(x, y, a, b);
}
bool cmp(Point p1, Point p2) {
	if (p1.x != p2.x) {
		return p1.x < p2.x;
	}
	return p1.y < p2.y;
}
bool isRightAngle(Point p1, Point p2, Point p3) {
	int x = (p1.x - p2.x)*(p1.x - p3.x) + (p1.y - p2.y)*(p1.y - p3.y);
	if (x == 0) {
		return true;
	}
	return false;
}
int distance(Point p1, Point p2) {
	return (p1.x - p2.x)*(p1.x - p2.x) + (p1.y - p2.y)*(p1.y - p2.y);
}
bool isSquare(Point p1,Point p2,Point p3,Point p4) {
	vector points(4);
	points[0] = p1;
	points[1] = p2;
	points[2] = p3;
	points[3] = p4;
	sort(points.begin(), points.end(), cmp);
	int s1 = distance(points[0],points[1]);
	int s2 = distance(points[0], points[2]);
	int s3 = distance(points[1], points[3]);
	int s4 = distance(points[2], points[3]);
	if (s1 == s2 && s2 == s3 && s3 == s4 && s1 != 0 && isRightAngle(points[0], points[1], points[2])) {
		return true;
	}
	else {
		return false;
	}
}


int main() 
{
	int N; cin >> N;
	vector nums(4);
	
	for (int index = 0; index < N; index++) {
		for (int i = 0; i < 4; i++) {
			cin >> nums[i].x >> nums[i].y >> nums[i].a >> nums[i].b;
		}
		int count = 0x3f3f3f3f;
		for (int m = 0; m < 4; m++) {
			for (int n = 0; n < 4; n++) {
				for (int p = 0; p < 4; p++) {
					for (int q = 0; q < 4; q++) {
						if (isSquare(rotate(nums[0], m), rotate(nums[1], n), rotate(nums[2], p), rotate(nums[3], q))) {
							count = min(count, m + n + p + q);
						}
					}
				}
			}
		}
		count = count == 0x3f3f3f3f ? -1 : count;
		cout << count << endl;
	}
	return 0;
}