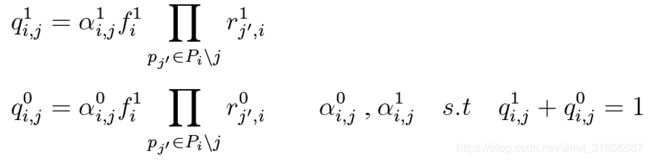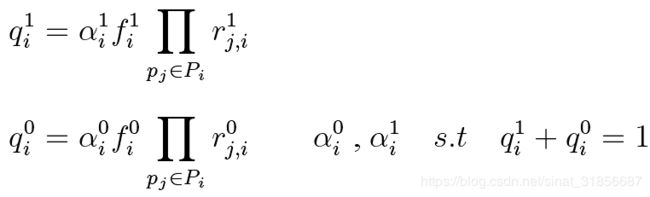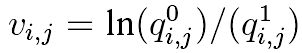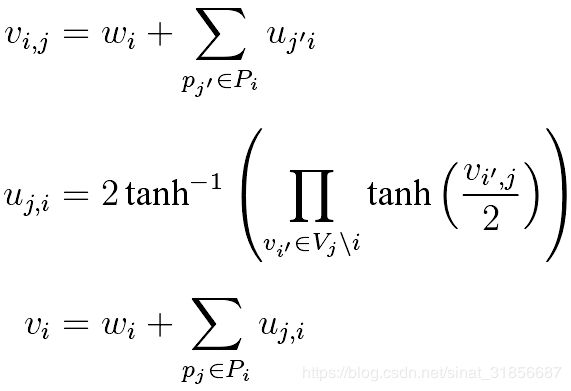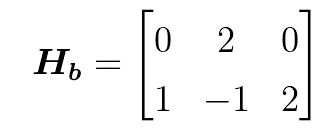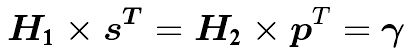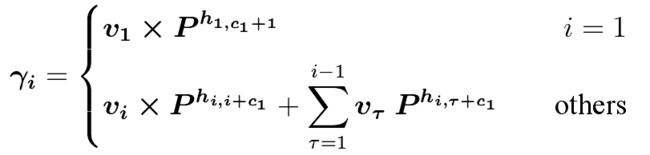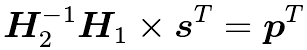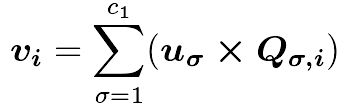LDPC码浅谈

香农限：就是在带宽一定、噪声已知（可以根据信道参数算出来）的情况下，一个传输信道能通过的有用的数据量上限能够接近信道所能容量的最大数据量，目前，符合5G网要求的就只有LDPC和Polar码。

LDPC：低密度校验码是一种高效的前向信道纠错码，由麻省理工学院Robert Gallager博士于1962年提出，是一种线性分组码，校验矩阵具有一定的稀疏性，具有无线接近香农限的良好性能。译码过程高效、复杂度和时延都比较低。

Polar：作为目前唯一可理论证明达到香农限，并且具有可使用的线性复杂度编译能力的信道编码技术。Polar码由土耳其教授Erdal Arikan在2008年提出。Polar码基于信道极化理论，在编码时将信道分为无噪信道和全噪信道，将有用的信息分到无噪信道，将垃圾信息分到全噪信道。因此在理论速度上，Polar码可以拥有无限逼近香农极限的速率，相比LDPC码，Polar码在网络性能更有优势，并且编码和译码的复杂度也比较低。

eMBB场景中，LDPC成为数据信道中编码长码，Polar成为控制信道中编码短码，因为数据以长码为主，控制信令以短码为主。

密度定义：校验矩阵中非零元素占据校验矩阵总元素的个数的比例，“低”一般指密度要低于0.5，并且码长越长，其“低密度”性越明显。

规则矩阵：校验矩阵每行列重相同，每列列重也相同，并且校验矩阵中任意两列中元素1位置相同的个数不能多于1个，这样的LDPC称为规则的，否则不规则。

校验矩阵：

二分图：

其中方形表示变量节点，其数量等于码长，即校验矩阵的列数；圆形是校验节点，数量与矩阵的行数相同，校验节点和变量节点之间通过边来连接；每个节点连接的边数称为度；粗线表示长为6的一个环，1-6环长为6，LDPC所有环的最小长度是LDPC的环。LDPC的环越长越好，说明从环中某变量节点发出的置信度信息被传递回自身的正反馈信息就越小，越有利于译码性能的提升。

 

 

LDPC常用译码算法：

硬判决算法：

用校验矩阵的每一行乘以编码后的转置码字，如果为0则停止译码，否则翻转参与校验失败最多的变量节点对应的比特，然后再重复计算，直到或者达到迭代次数。

软判决译码：基于置信度（BP）传播算法

通过在变量节点和校验节点之间传播和更新置信度信息来达到译码收敛的效果。

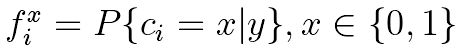表示仅根据信道特性和接收向量而不考虑比特间的校验相关性而得出的后验概率，且有，变量节点v传递给校验节点p的信息记为q，校验节点p传递给节点v的信息位r，每次迭代根绝q和f计算伪后验概率，

译码开始的时候，，其后变量节点v根据下式对q进行更新，

校验节点p根据下式进行更新：

每次迭代结束后求出q

如果，则译出的比特为1，否则为0。整个计算只涉及求和和乘积运算，所以BP算法又称为和积译码。

使用LLR-BP算法对齐进行简化，记，则上述式子可以变为

进一步简化：

上面是最小和译码算法MSA。

衍生算法：归一化最小和算法

加入了一个权重因子α

偏置最小和算法：

加入一个偏置因子β

准循环LDPC（QC-LDPC）：

LDPC校验矩阵主要有随机化生成法和结构化生成法，准循环LDPC就是通过循环置换矩阵的结构化构造方法构造出的一类LDPC，更有利于编码和译码。现已被用在5G  eMBB场景中采用。

校验矩阵构造过程为：

Hb是由前面矩阵的幂次构成维度为rxc的矩阵，例子：

，Z=3

扩展为mxn=6x9

QC-LDPC由基础矩阵和扩展因子唯一确定。基础矩阵中的数字表示的是校验矩阵中的单位矩阵移位的次数，h为-1时矩阵为o，h的取值为【-1，Z-1】。矩阵中P行重和列重都为1时为单边QC-LDPC，否则为多边QC-LDPC，在码率较高时，多边构造法可以通过增加行重和列重来提升性能，相比单边构造法，多边QC-LDPC译码性能要好0.15dB，但同时译码复杂度也要比单边QC-LDPC高。

802.11ad标准中规定的QC-LDPC一共有四种码率、码长为672比特的LDPC，下面是码率为3/4时对应的基础矩阵

LDPC通用的编码算法：

主要有高斯消元法以及近似下三角矩阵法

高斯消元法利用高斯消元来通过校验矩阵H求取生成矩阵G，然后通过c=sG的方法求出编码码字c。消元的过程会丧失掉校验矩阵的稀疏性，不利于编码实现；常用的编码算法为近似下三角矩阵法，该算法直接通过校验矩阵求取编码码字的校验比特位。

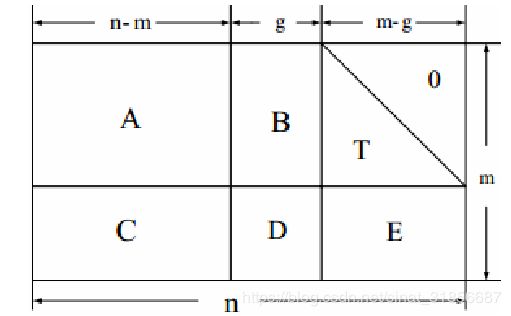
首先，将校验矩阵变换为下图的下三角形式

其中，T为下三角矩阵，然后通过校验矩阵的每一行乘以转置后的码字乘积为0以及下式可以得到后面两个式子：

其中，I为单位矩阵，，通过中间的式子求出校验比特部分p1，进而带入最后的式子求得校验比特p2以完成编码。

QC-LDPC编码算法：

因为LDPC属于线性分组码，对于线性分组码的编码核心就是根据校验矩阵或者生成矩阵计算出p向量。

生成矩阵法：

，c=[s,p]

s为信息比特部分，p为校验比特部分，p=sQ

还可以直接利用QC-LDPC的校验矩阵直接计算出校验位：

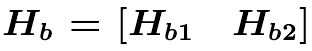，其中Hb1的大小为rxc1，Hb2的大小为rxr，c1=c-r

对应的扩展矩阵分块表示为

，其中H1的大小为mxn1，H2的大小为mxm，n1=n-m。

其中H1、H2和s均是已知的，根据最后一个式子可推算出校验比特向量p。

令

将上面最后一个式子左边展开可得γ

将上面的式子进一步变形

算法与生成矩阵的关系是

将Q矩阵分块为

那么由可以得到

这种算法也只需要移位或者异或