【离线渲染】自适应光子映射(一):光子映射算法和梅特波利斯算法简述
本文来自PBRT的一个课后习题,自适应光子映射算法主要适用于摄像机只观察场景中的一小部分的情况,该算法结合了光子映射算法和梅特波利斯算法,所以在这一节我们会对这两种算法进行一个简单的介绍。
目录
1.1路径追踪
1.2光子映射
1.3渐进式光子映射
1.4随机渐进式光子映射
1.5光子映射方法总结
2.1蒙特卡罗
2.2Metropolis Light Transport
2.3Primary Sample Space Sampler
2.4Multiplexed MLT
2.5MLT算法总结
1.1路径追踪
路径追踪的主要问题是噪点非常严重,它需要非常多的样本才能解决这个问题,而对于一些小概率路径,比如SDS路径,则很难被路径追踪方式采样到,并且,对存在大量漫反射的场景进行采样时,需要很多的采样路径,这同样造成了噪点严重。


图左使用的是路径追踪,图右使用的是随机渐进式光子映射[来自PBRT]
1.2光子映射
光子映射算法(PhotonMapping)则解决了这个问题,传统的PM算法由两部分组成:
第一部分是光源路径,主要操作为1.从光源发射光子,光子在场景中迭代地进行反射/折射/吸收,光子在和场景中的漫反射表面相交时被记录下来,并存储在一个光子图中。
2.如果光子击中一个漫反射表面,该光子会从光子交点的半空间中随机选择一个反射方向进行传播,对于其他表面则根据brdf分布进行重要性采样。
3.通过俄罗斯轮盘来决定光子路径是否被中止。
//PBRT
Float q = std::max((Float)0, 1 - bnew.y() / beta.y());
if (RadicalInverse(haltonDim++, haltonIndex) < q) break;第二部分是摄像机路径
从摄像机发出观察光线,如果第一次相交的表面为漫反射面,则该光线的光照贡献可以直接通过光子图进行估计,如果第一个相交的面为镜面或光泽面,则使用一般的光线追踪方法发射新的光线,重复此步骤直到遇到漫反射表面
1.3渐进式光子映射
传统光子映射的的一个缺点是,由于所有的光子都需要被存储,所以光子的数量受限于可用内存容量。渐进式光子映射(Progressive Photon Mapping)通过重构PM算法解决了该问题。
相比PM,PPM的两个步骤恰好相反,PPM首先从相机发射光线,每个像素存储了所有从该像素发出的光线与非光泽表面的交点。第二部分从光源发射光子,在光子和每一个表面的交点处,计算该光子对附近可视点的贡献。同时PPM将第二阶段拆分成多个迭代地过程,每个过程只需要存储少量的光子,因此整个迭代地过程可以任意提高光子的数量。并随着迭代步骤的增加,减少从相机发出的可视点的搜索半径。
1.4随机渐进式光子映射
PPM只能计算一个固定可视点的值,但是在渲染中,我们常常需要计算一个区域的辐射亮度,比如抗锯齿,景深,运动模糊的实现。
随机渐进式光子映射(SPPM)通过一个很小的改进解决了这个问题。相对于ppm对每个可视点存储一组统计变量,sppm则对每个区域(一或多个像素)使用一组共享的统计变量。其余部分和PM大致相同。
//PBRT中像素的定义
struct SPPMPixel {
// SPPMPixel Public Methods
SPPMPixel() : M(0) {}
// SPPMPixel Public Data
Float radius = 0;//共享半径
Spectrum Ld;//直接光照贡献
struct VisiblePoint {
// VisiblePoint Public Methods
VisiblePoint() {}
VisiblePoint(const Point3f &p, const Vector3f &wo, const BSDF *bsdf,
const Spectrum &beta)
: p(p), wo(wo), bsdf(bsdf), beta(beta) {}
Point3f p;
Vector3f wo;//可视点对应反射光线的方向
const BSDF *bsdf = nullptr;//可视点的BRDF
Spectrum beta;
} vp;//可视点
AtomicFloat Phi[Spectrum::nSamples];
std::atomic M;
Float N = 0;
Spectrum tau;//共享累积辐射通量
}; 对于光子追踪部分,当越来越多的光子对某个可视点作出贡献时,我们则渐进地收缩该可视点检测光子的半径,而减少半径需要基于反射辐射亮度来进行计算。式子如下
![]()
\\Code In PBRT
Float gamma = (Float)2 / (Float)3;
Float Nnew = p.N + gamma * p.M;
Float Rnew = p.radius * std::sqrt(Nnew / (p.N + p.M));
Spectrum Phi;
for (int j = 0; j < Spectrum::nSamples; ++j)
Phi[j] = p.Phi[j];
p.tau = (p.tau + p.vp.beta * Phi) * (Rnew * Rnew) /
(p.radius * p.radius);
p.N = Nnew;
p.radius = Rnew;
p.M = 0;![]() 是第i次迭代后对该区域作出贡献的光子数量
是第i次迭代后对该区域作出贡献的光子数量
![]() 是当前迭代对该区域做出贡献的光子数量
是当前迭代对该区域做出贡献的光子数量
![]() 是第i次的搜索半径
是第i次的搜索半径
![]() 是共享辐射累积通量
是共享辐射累积通量
这里的![]() 是一个区域的共享属性,而不是一个可视点的共享属性
是一个区域的共享属性,而不是一个可视点的共享属性
Spectrum Phi =
beta * pixel.vp.bsdf->f(pixel.vp.wo, wi);
for (int i = 0; i < Spectrum::nSamples; ++i)
pixel.Phi[i].Add(Phi[i]);
++pixel.M;1.5光子映射方法总结
2.1蒙特卡罗
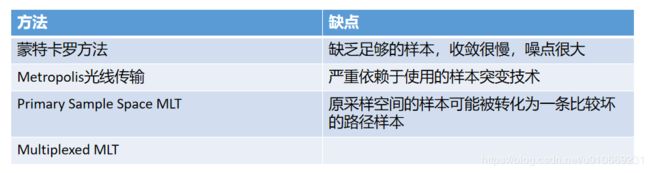
传统的蒙特卡罗方法能够根据一个已知的概率密度分布进行p进行路径采样,然而受限于p并不能完全近似未知的目标函数分布,对于一些在p中概率很小然而f贡献值却很大的路径,传统的蒙特卡罗方法由于缺乏足够的样本,会导致收敛很慢,噪点很大,此时,另一种不依赖于构建一个假想概率密度的马尔科夫链蒙特卡罗方法则是一个更加有效的选择。
左:路径追踪 右:Metropolis
2.2Metropolis Light Transport
因为不依赖于任何概率分布,梅特波利斯光线传输(MLT)算法中的样本是任意分布的,梅特波利斯算法根据样本之间的相关性来使样本集合服从目标函数的分布,这使得MLT算法能够处理如此可见性比较复杂的场景,然而其收敛效率严重依赖于使用的样本突变技术,糟糕的突变技术将大大降低突变样本的接受率,而使得收敛速度非常缓慢。
\\Metropolis Algorithm
if (rng.UniformFloat() < accept) {
pCurrent = pProposed;
LCurrent = LProposed;
sampler.Accept();
++acceptedMutations;
} else
sampler.Reject();2.3Primary Sample Space Sampler
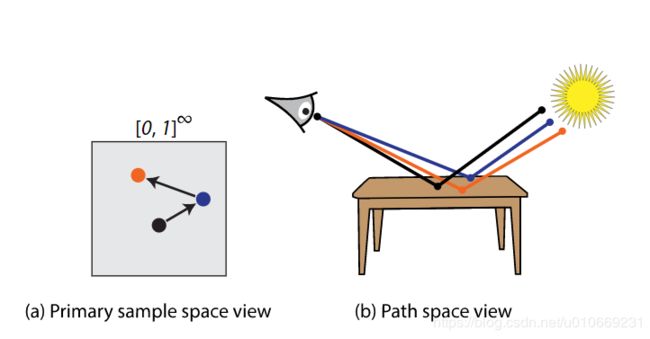
为了减少路径样本的方差,原采样空间MLT(PSSMLT)提出了直接在路径的原采样空间进行突变,由于原采样空间的贡献值函数更为平摊,因此样本的理论接受率理论上可以得到较大的提升。
传统的路径采样的过程是增量式的,它首先从光源(或摄像机)选择一个起始点,然后让光线在场景中传播,直到与摄像机(或光源)相遇,在这个过程中每个步骤都会产生一个或多个随机数,例如选择随机像素上起点的位置,根据表面顶点BSDF属性随机选择反射或折射方向,以及根据俄罗斯概率轮盘随机选择中止概率等等。
在上述过程中,如果每一步都使用逆变换算法,则每一个步骤的单次采样,都可以转化为对一个或多个【0,1】均匀分布采样,将整个路径采样过程中每个单个的采样过程组合起来,则构成一个高维的单位超立方体,由于该空间提供了所有的随机数来源,我们称该立方体构成的空间为原采样空间。
Float MLTSampler::Get1D() {
ProfilePhase _(Prof::GetSample);
int index = GetNextIndex();
EnsureReady(index);
return X[index].value;
}
Point2f MLTSampler::Get2D() { return {Get1D(), Get1D()}; }上述代码为PBRT中MLTSampler提供随机数的代码,所有的随机数都来自X,即原采样空间,每次获得样本后索引加一。
使用该采样器的函数举例:
int lightNum = lightDistr.SampleDiscrete(sampler.Get1D(), &lightPdf);
Spectrum Le = light->Sample_Le(sampler.Get2D(), sampler.Get2D(), time, &ray,
&nLight, &pdfPos, &pdfDir);
if (ray.medium) beta *= ray.medium->Sample(ray, sampler, arena, &mi);
pdfFwd = pdfRev = mi.phase->Sample_p(-ray.d, &wi, sampler.Get2D());
Spectrum f = isect.bsdf->Sample_f(wo, &wi, sampler.Get2D(), &pdfFwd,BSDF_ALL, &type);
Spectrum Wi = camera.Sample_Wi(qs.GetInteraction(), sampler.Get2D(), &wi, &pdf, pRaster, &vis);2.4Multiplexed MLT
然而PSSMLT算法虽然在原采样空间产生了比较好的突变样本但这并不是直接的路径样本,而需要通过一个映射将原采样空间的样本转化为一条路径,由于它将路径看做一个黑盒子,因此原采样空间的样本可能被转化为一条比较好或坏的路径样本,由于一条原采样空间的样本可以被双向路径转化为多条路径,这就可能导致好的原采样空间样本被映射到比较糟糕的路径样本。
MMLT算法通过增加一个长度路径控制参数,来使路径被限定为固定的长度,然后通过不同子路径的组合间接达到了选择不同采样技术的目的。
PBRT中代码如下:
Spectrum MLTIntegrator::L(const Scene &scene, MemoryArena &arena,
const std::unique_ptr &lightDistr,
const std::unordered_map &lightToIndex,
MLTSampler &sampler, int depth, Point2f *pRaster) {
sampler.StartStream(cameraStreamIndex);
// Determine the number of available strategies and pick a specific one
int s, t, nStrategies;
if (depth == 0) {
nStrategies = 1;
s = 0;
t = 2;
} else {
nStrategies = depth + 2;
s = std::min((int)(sampler.Get1D() * nStrategies), nStrategies - 1);
t = nStrategies - s;
}
// Generate a camera subpath with exactly _t_ vertices
Vertex *cameraVertices = arena.Alloc(t);
Bounds2f sampleBounds = (Bounds2f)camera->film->GetSampleBounds();
*pRaster = sampleBounds.Lerp(sampler.Get2D());
if (GenerateCameraSubpath(scene, sampler, arena, t, *camera, *pRaster,
cameraVertices) != t)
return Spectrum(0.f);
// Generate a light subpath with exactly _s_ vertices
sampler.StartStream(lightStreamIndex);
Vertex *lightVertices = arena.Alloc(s);
if (GenerateLightSubpath(scene, sampler, arena, s, cameraVertices[0].time(),
*lightDistr, lightToIndex, lightVertices) != s)
return Spectrum(0.f);
// Execute connection strategy and return the radiance estimate
sampler.StartStream(connectionStreamIndex);
return ConnectBDPT(scene, lightVertices, cameraVertices, s, t, *lightDistr,
lightToIndex, *camera, sampler, pRaster) *
nStrategies;
} 对于一个给定长度为k的链,MMLT算法首先对【0,1】执行一个均匀采样,然后将得到的浮点结果映射到该路径对应的顶点数量k+2,并得到一个表示其中一个子路径顶点数量的整数值t。然后计算另一个子路径的长度s=(k+1)-t,它们分别被用于双向路径追踪中的摄像机子路径和光源子路径采样。
if (GenerateCameraSubpath(scene, sampler, arena, t, *camera, *pRaster,
cameraVertices) != t)
return Spectrum(0.f);我们只需要特定长度的路径,如果不是的话就返回0.
return ConnectBDPT(scene, lightVertices, cameraVertices, s, t, *lightDistr,
lightToIndex, *camera, sampler, pRaster) *
nStrategies;按照策略s t进行连接。这个按照随机选择的策略连接的完整路径的贡献相当于原本所有课程n条完整路径的贡献的平均值,所以最终返回的贡献需成以nStrategies
2.5MLT算法总结
REFERENCES:
- Hachisuka, T., and H. W. Jensen. Robust adaptive photon tracing using photon path visibility. ACM Transactions on Graphics 30 (5), 114:1–114:11.
- Physically Based Rendring :From Theory To Implementation
- 全局光照技术:从离线到实时渲染