Python实现经典排序算法--快速排序

网络上用python实现快速排序有四种实现方式，有用匿名函数lambda表达式和双重循环实现的，也有用栈实现非递归的排序，这里我只讲一讲利用算法导论里面的分治思想，迭代来实现序列的快速排序。

分治策略是对于一个规模为n的问题，若该问题可以容易地解决（比如说规模n较小）则直接解决，否则将其分解为k个规模较小的子问题，这些子问题互相独立且与原问题形式相同，递归地解这些子问题，然后将各子问题的解合并得到原问题的解。

即分解，解决，合并。

第一步分解：将数组list[p,r]分解为两个可能为空的子数组list[p,q-1],list[q+1,r],使得子数组1中所有元素均小于list[q]，子数组2中的所有元素均大于list[q]，而计算下标q是划分过程的一部分。

第二部解决：通过递归调用快速排序，对子数组进行排序，递归至子数组为为1个元素或为空，即递归结束。

第三部合并：因为子数列都是原址排序，故不需要合并。

故利用分治策略解决快速排序的问题就是分解和解决的问题，最核心的步骤则是在于分解。

分解：分为三个步骤：初始化，维护，终止。

初始化：这里我们可以根据需求定义四个子空间[p,i]，[i+1,j]，[j+1,r-1]，[r]，依次为小于list[r]的空间，大于等于list[r]的空间，待排序的空间以及基准空间（只有一个基准元素list[r]）。

维护：我们构建一个维护过程，即给定一个任意序列，通过交换顺序来维护快速排序的性质，将序列的元素放入四个空间内。

终止：也就是当j=r时，此时序列已经有序了。

这里需要对序列进行划分，而划分边界q很明显可以知道是i+1，q=i+1这里我们把基准元素和下标i+1对应的元素进行替换，可以得到新序列。而新序列中下标q对应的位置即为正确位置。左边迭代可以获取左边所有元素的正确位置，右边迭代可以获取右边所有元素的正确位置。当所有迭代完成后，该序列即完成了排序。其算法在最不利情况下的时间复杂度为 紧渐近于n^2,但是其平均性能特别好，对应的期望时间复杂度为紧渐近于n*lg n，而且还是原址排序，所以该算法应用的范围特别广。

下面是用Pyhton是实现的code：

def quicksort(list,p,r):
	if p

out：[1,2,3,4,5,6,7,8]

来分析一下上面的算法过程,最重要的还是划分过程。在partion函数里面，我们初始化i=-1，p=0,r=7,j从0至7，这里有一个循环过程，就是拿序列里面的八个元素与第八个元素（基准元素）进行比较，如果元素小于基准元素，i+=1，置换list[i]和list[j]的顺序，当j=0时，就是list[0]与list[0]置换，这里不变，但是第一个子空间已经增大了一个元素，list[0]<=list[r]；当j=1时，list[1]>=list[r]，此时不交换任何位置，但第二个子空间会随着j的增大而增加一个元素，而此时的第三个子空间已经减少了两个元素了。依次的当j=6时，list[6]>=list[r]，不交换任何位置，而第三个子空间已经没有任何元素了。当j=7时，list[7]>=list[r]，不交换任何位置。此时循环结束，调换list[r]与list[i+1]，使得list[r]可以获取正确的位置，并返回i+=1为划分边界q。

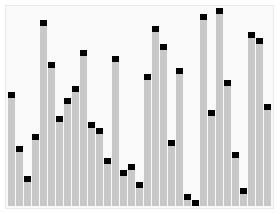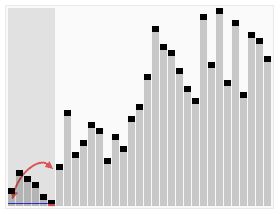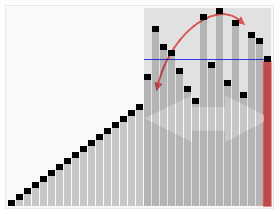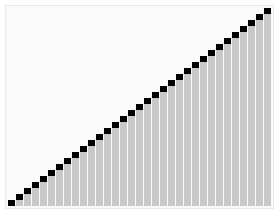
下面将计算结果可视化：

详细过程如下：

def quicksort(list,p,r):
	if p

out:

+ [2, 8, 7, 1, 3, 5, 6, 4] +
+ [2, 8, 7, 1, 3, 5, 6, 4] +
+ [2, 8, 7, 1, 3, 5, 6, 4] +
+ [2, 1, 7, 8, 3, 5, 6, 4] +
+ [2, 1, 3, 8, 7, 5, 6, 4] +
+ [2, 1, 3, 8, 7, 5, 6, 4] +
+ [2, 1, 3, 8, 7, 5, 6, 4] +
+ [2, 1, 3, 4, 7, 5, 6, 8] +
+ [2, 1, 3, 4, 7, 5, 6, 8] +
+ [2, 1, 3, 4, 7, 5, 6, 8] +
+ [1, 2, 3, 4, 7, 5, 6, 8] +
+ [1, 2, 3, 4, 7, 5, 6, 8] +
+ [1, 2, 3, 4, 7, 5, 6, 8] +
+ [1, 2, 3, 4, 7, 5, 6, 8] +
+ [1, 2, 3, 4, 5, 7, 6, 8] +
[1, 2, 3, 4, 5, 6, 7, 8]