二叉堆与堆排序

   这篇博文对二叉堆有了很好的解读与阐述，在此根据自己的理解整理如下。

二叉堆的定义

   二叉堆，本质上是一棵完全二叉树。
   二叉堆满足两个特性：

1. 父结点的键值总是大于或等于(小于或等于)任何一个子节点的键值。
2. 每个结点的左子树和右子树都是一个二叉堆(都是大顶堆或小顶堆)。

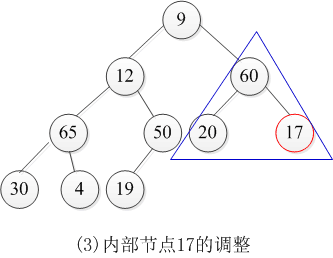
   当父结点的键值总是大于或等于任何一个子结点的键值时，堆为大顶堆(最大堆)；当父结点的键值总是小于或等于任何一个子结点的键值时，堆为小顶堆(最小堆)。下图所示为一个最小堆：

二叉堆的存储

   因为二叉堆的本质就是一棵完全二叉树，因此，一般直接用数组来表示二叉堆。相应的，就有一些结论：

• 结点i的父结点为结点(i-1)/2
• 结点i的子结点分别为(2*i+1)和(2*i-1)
• 含有n个结点的二叉堆中，最后一个内部结点即为最后一个结点(n-1)的父结点(n/2-1)

二叉堆的操作

   二叉堆的操作主要包括三种：建立、插入、删除。

1. 堆的建立。给定一个数组，对应一棵完全二叉树，根据堆的定义，对数组中的元素进行冲排序，使得排序后的二叉树满足堆的条件，成为一棵“堆化”的树。下图所示为一个简单的堆的建立过程：
   

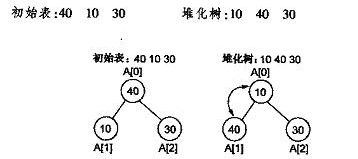
2. 堆的插入。每次插入一个新元素时，都直将新数据插入到数组的最后，然后根据堆的定义进行调整以恢复堆次序。值得注意的是，在二叉堆中，从根结点到任何一个结点的路径上的所有结点都是有序的，那么从根结点到新结点的父结点的路径上的结点都必然有序，只要将新结点放到这个有序序列中恰当的位置，就可以保证树的“堆性”，这一个过程其实类似于一个插入排序的过程。调整时，如果新结点的键值大于其父结点，则将新结点与其父结点调换位置，并继续将新结点与其新的父结点进行比较，直至与根结点比较完毕；如果在调整过程中，某一时刻，父结点的键值大于或等于新结点的键值，则说明此路径已经有序，调整完成。下图所示为一个插入新结点的过程：
   

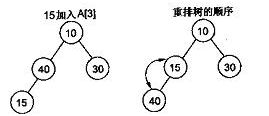
3. 堆的删除。堆的删除每次只能删除根结点，也就是第0个数据。为了便于重建堆，实际操作时，会将最后一个结点的值赋给根结点，然后再从根结点开始作依次自顶向下的调整。调整时，先找出左右儿子结点中较大的一个，如果父结点小于这个较大值，则交换父结点与较大的子结点，直至父结点“下沉”为了叶子结点；在根结点“下沉”的过程中，如果某一时刻父结点的键值大于或等于子结点的键值，则表明此时堆已经重建完成，调整过程结束。下图所示为堆的删除：
   

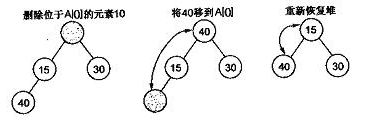
堆化数组

   数组的堆化，其实就是堆的建立过程。对于一个给定的数组，我们可以得到一棵初始的完全二叉树，接下来就是调整的过程。

   很明显，对于每一个叶子结点，可以认为它是一个合法的堆。

   从最后一个内部结点k开始调整，可以看到，对于以k为跟结点的子树而言，k的左右子树已经堆化，完成根结点k的“下沉”即可堆化以k为根结点的子树。接着处理前一个内部结点，直到根结点处理完毕，数组的堆化过程也完成了。

   举个例子说明一下。如下图，有一个数组int A[10] = {9、12、17、30、50、20、60、65、4、49}，

   初始时刻，叶子结点20、60、65、4、19都是合法的堆；从最后一个内部结点50开始调整。调整过程如下：

   至此，数组的堆化完成。(此时的堆是一个大顶堆)

二叉堆的应用——堆排序

   到目前为止，二叉堆的主要应用好像就是用于作排序。可以看到，对于一个数组，堆化为大顶堆后，根结点的键值(第0个数据)就是数组中最大的元素，依次删除根结点，就能够依次找到剩余数据中最大的元素，即依次删除的结点是有序的。

   由于堆本身也是用数组模拟的，在实际排序时，第一次将A[0]与A[n-1]交换，再对A[0,n-2]重新恢复堆，这样一来，原数组中最大的元素即为数组中最后一个元素，与此同时，新堆中根结点为原数组中第二大的元素；第二次将A[0]与A[n-2]交换，再对A[0,n-3]重新恢复堆，其结果是原数组中最大的元素为数组中倒数第二个元素，同时新堆的根结点为原数组中第三大的元素……重复这一删除与恢复的过程，待堆中仅剩一个结点时，数组中的元素就完成了升序排序。(如果排序过程中将数组堆化为小顶堆，那么最终排序的结果是降序序列。)

   建立堆时，共需进行N/2次向下的调整，每次调整的时间复杂度为O(logN)，因此建立堆的时间复杂度为O(NlogN)；进行排序时，由于每次重新恢复堆的时间复杂度为O(logN)，共进行N-1次重新恢复操作，所以进行排序的时间复杂度为O(NlogN)。总的说来，对一个数组进行堆排序，时间复杂度为O(NlogN)。

---

代码实现

   MaxHeap.h中定义了一个类，该类实现了堆的定义及堆的相关操作。类中，int型指针data用于存储堆中的元素，size和increment则用于控制data所指向的存储区的大小，number用于保存堆中实际的结点个数。

MaxHeap.h

#ifndef _MAXHEAP_H_
#define _MAXHEAP_H_

#include 
#include 
#include 
#include 
#include 
using namespace std;

#define INISIZE 10
#define INIINCREMENT    10

class MaxHeap {
public:
    int size;
    int number;
    int increment;
    int * data;

    MaxHeap(int * iniArray, int n, int size = INISIZE, int increment = INIINCREMENT);
    ~MaxHeap();
    void insertNode(int newNum);    
    void deleteNode();
    int * maxHeapSort(int& count); 
    void printHeap();    //打印堆中所有的结点键值，主要用于调试

private:
    void initMaxHeap();
    void fixup();                    //完成结点向上的调整
    void fixdown(int rIndex);        //完成结点向下的调整
    void swap(int& m,int& n);
    int max(int i,int j,int& index);
};

MaxHeap::MaxHeap(int *iniArray, int n, int size, int increment)
{
    if(n > size) {
        this->size = n;
    } else {
        this->size = size;
    }
    this->increment = increment;
    data = (int *)malloc(sizeof(int) * this->size);
    memset(data, 0, this->size);
    if (iniArray == NULL) {
        number = 0;
    } else {
        memcpy(data, iniArray, n*sizeof(int));
        number = n;
    }
    initMaxHeap();
}

MaxHeap::~MaxHeap()
{
    if (data) {
        free(data);
    }
}

void MaxHeap::initMaxHeap()
{
    int i;
    if (number == 0) {
        return ;
    }
    for (i=number/2-1;i>=0;i--) {
        fixdown(i);
    }

}

void MaxHeap::fixup()
{
    int i = number-1;
    int j;
    j = (i-1)/2;
    while ((j>=0) && (i>0)) {
        if (data[j]1)/2;
        } else {
            break;
        }
    }
}

void MaxHeap::insertNode(int newNum)
{
    if (number >= size) {
        size += increment;
        data = (int *)realloc(data,sizeof(int)*size);
    }
    data[number] = newNum;
    number ++;
    fixup();
}

void MaxHeap::fixdown(int rIndex)
{
    int index;
    int i=rIndex;
    while ((2*i+1)if (data[i] < max(2*i+1,2*i+2,index)) {
            swap(data[i],data[index]);
            i = index;
        } else {
            break;
        }
    }
}

void MaxHeap::deleteNode()
{
    if (number == 0) {
        return;
    }
    swap(data[0],data[number-1]);
    number --;
    fixdown(0);
}

int * MaxHeap::maxHeapSort(int& count)
{
    count = number;
    int i = number-1;
    while (i>=0) {
        deleteNode();
        i --;
    }
    return data;
}

void MaxHeap::swap(int& m,int& n)
{
    m = m^n;
    n = m^n;
    m = m^n;
}

int MaxHeap::max(int i,int j,int& index)
{
    if (j >= number) {
        index = i;
    } else if (data[i]>data[j]) {
        index = i;
    } else {
        index = j;
    }
    return data[index];
}

void MaxHeap::printHeap()
{
    int i;
    for(i=0;icout << setw(5) << left << data[i];
    }
    cout << endl;
}
#endif

test.cpp

#include "MaxHeap.h"

int main()
{
    int count;
    int * sorted;
    int n = 100;
    int iniArray[] = {9,12,17,30,50,20,60,65,4,49};
    int length = sizeof(iniArray)/sizeof(int);
    MaxHeap myHeap(iniArray,length);
    cout << "初始时刻：" << endl;
    myHeap.printHeap();
    myHeap.insertNode(n);
    cout << "插入结点100：" << endl;
    myHeap.printHeap();
    myHeap.deleteNode();
    cout << "一次删除后：" << endl;
    myHeap.printHeap();
    sorted = myHeap.maxHeapSort(count);
    cout << "堆排序后：" << endl;
    for (int i=0;icout << left << setw(5) << sorted[i];
    }
    cout << endl;

    return 0;
}

输出结果

   小贴士

1. 关于默认参数的函数，在声明时要给参数赋默认值，但是在定义时，千万不要再给参数赋默认值，否则将编译报错“重定义默认参数”。

2. cout的输出小技巧。为了使cout的输出格式更规范，除了可以使用"\t"、"\n"等转义字符外，还可以使用std::setw(n)设置输出宽度为n(默认是右对齐)，还可以使用std::left设置输出为左对齐，或者使用std::right设置输出为右对齐。如果指定了名字空间为std，切包含了 和头文件，则可以直接设置。
   e.g.
      cout << left << setw(5) << i << endl; 设置输出为左对齐，输出宽度为5