速度和性能，我全都要，从头训练稀疏网络：不损失性能的快速训练

点击上方“AI公园”，关注公众号，选择加“星标“或“置顶”

---

作者：Tim Dettmers

编译：ronghuaiyang

导读

一种训练稀疏网络的方法，不需要重训练，一次完成，又快速，又不损失性能，边缘设备部署必备。

这篇博客文章是关于我和 Luke Zettlemoyer 的工作，Sparse Networks from Scratch: Faster Training without Losing Performance^[1]，目的是使用神经网络快速训练，在整个训练中我们保持网络的稀疏。我们证明，通过开发一个算法，稀疏动量，我们可以初始化一个具有稀疏随机权值的神经网络，并将其训练到和密集网络相当的性能级别 — 而这一切只需要进行一次训练。此外，如果我们使用优化的稀疏卷积算法，我们可以训练在 VGG 时得到 3.5x 的加速，在 Wide Residual 网络上得到 12x 的加速。这与彩票假设(Frankle 和 Carbin, 2019)和其他工作中使用的需要重复剪枝和再训练周期的计算昂贵的方法形成了鲜明的对比。因此，我们证明了将稀疏网络训练到和密集网络相当的性能级别不需要“赢得初始化彩票”，但是如果结合一种巧妙地在网络中移动权值的方法，则可以通过随机权值可靠地完成。我们称这种在整个训练过程中保持稀疏性同时又保持密集的表现水平的范式为“稀疏学习”。虽然这项工作表明了稀疏学习是可能的，但未来的工作有望在需要与当前密集网络相同或更少计算资源的情况下，在更多数据上训练更大、更深的网络。

为什么需要稀疏学习？

深度学习的一个重要推动因素是计算资源的进步。从 2010 年到 2018 年，我们看到计算 GPU 性能提高了 9700%。然而，由于达到了半导体技术的物理极限，我们可以预期在未来 5-8 年内，GPU 性能的提高将略高于 80%。如果我们不能进一步提高计算能力，研究世界会是什么样子？

这一点可以从自然语言处理(NLP)社区中窥见一斑，在这个社区中，像 ELMO、GPT、BERT、GPT-2、Grover 和 XL-Net 这样的预训练过的语言模型通过在大多数 NLP 任务中胜过其他方法而统治了整个领域。这些模型通常相当简单：你在大量的文档上训练它们，任务主要是预测给定一系列其他单词的单词 — 有点像做填空题。懂了吗？这些模型太大了，以至于需要超过 100 个 gpu 小时来训练。这对于那些想要了解这些模型但却无法做到的学术研究人员来说尤其令人沮丧，因为他们缺乏大公司所拥有的计算资源。为了真正理解这些大量的预先训练过的语言模型，一个主要的目标应该是通过开发更多的训练程序来大众化这些模型的训练。

实现这一目标的一种方法是通过观察人类大脑来寻找灵感。人脑消耗的能量是 GPU 的十分之一，但却要比 GPU 强大 10^9 倍。是什么使得大脑的计算效率如此之高？原因有很多，但其中一个原因是“稀疏性”。

研究发现，灵长类大脑中的神经元越多，普通神经元与其他神经元之间的连接就越少(Herculano-Houzel 等，2010)。这与我们设计深度神经网络的方式大相径庭，深度神经网络是将一层中的每个新神经元与上一层中的所有神经元连接起来。我们已经知道如何将一个完全训练好的密集网络压缩成一个稀疏网络(Han et al.， 2015)，但是，如果一个人从一个我们在训练时保持稀疏的稀疏网络出发，那么如何成功地做到这一点却鲜有研究。我们怎么做呢？

稀疏动量：训练稀疏网络的一个高效的方法

本节解释了稀疏动量算法的直觉到完整算法的过程。

图1：稀疏动量通过查看最近梯度(动量)的加权平均值来确定在稀疏网络中何处增加新的权值，从而找到一致降低误差的权值和层数。(1)根据平均动量幅值大小确定各层的重要性。(2)对于每一层，我们去掉50%的最小权值。(3)然后根据层的重要性在层之间重新分配权重。在一层中，我们在动量幅值大小较大的地方增加权重。

好的稀疏学习算法主要具有什么样的性质？

在稀疏学习中，最重要的是尽可能有效地利用神经网络中的每一个权值。如果你将“有效性”定义为“减少错误”，那么对于如何进行，我们就有了一个明显的观点。我们需要找到一种方法来描述一个权重在减少误差方面有多有效，并去掉所有不有效的权重。一旦我们删除了权值，我们希望在我们认为有希望在未来减少错误的位置重新生成新的权值。

如果我们看一下误差的梯度和权值的关系，我们实际上有一个精确的度量。然而，如果我们观察连续的梯度，我们会发现梯度可以剧烈地振荡。例如，如果你有一个分类手写数字 0 到 9 的神经网络，然后某个权值可能擅长发现顶部的直线，那么，它可能有助于减少数字 5 和 7 的错误，它也可能没有帮助，甚至对数字 0,1,2,3,6,8,9 是有害的。相反，检测右上角的曲线模式的权重可能有助于 0、2、3、8、9，因此，我们希望这个权重随着时间的推移比“顶部的直线”的权重更可以持续地减少错误。我们如何在神经网络中自动检测这些有前途的权重呢？

动量: 找到持续减少误差的权重

如果你把北极当作局部最小值，把指南针当作指向局部最小值的梯度，那么你就可以通过疯狂摇动指南针来模拟随机梯度下降更新。当指针每次经过北极时，它会减速，然后越来越接近的指向北极，然而，由于自旋，它仍然会“过”那个方向。因此，当磁针仍在来回移动时，从两三次测量中可能不清楚北极在哪里。然而，如果你使用平均方向 — 一次针有点左边的北极，另一次偏右边一点的，那么把这些偏差消掉了之后，你会马上得到一个方向非常接近真正的北极。

这是动量优化技术背后的主要思想：我们平均连续的梯度，以获得一个更好的估计方向的局部最小值。类似于罗盘指针，当它慢下来时，会随着时间变得越来越精确，我们希望在随机梯度下降中对最近的梯度方向给予更高的权重。一种方法是分配一个加权平均值，其中我们分配一个大得多的权重给当前梯度，一个小得多的权重给以前的梯度——这叫做指数平滑。通过指数平滑权值的梯度，我们得到了一个加权梯度矩阵——这个矩阵就是动量矩阵。通过这种方法，我们可以确定哪些权重可以持续地减少误差。

重新分配权重：每一层的平均动量幅值

从这里我们得到了稀疏动量算法的第一个重要观察：如果一个权值的动量显示它能够持续减少误差的多少，那么一层中所有权值的平均动量的大小就显示了这一层能够减少错误的平均能力。我们取幅值大小是因为两个不同的权值可能一致地向着负方向和正方向。通过计算各层的平均动量大小，我们可以很容易地比较各层的平均权重的效果。例如，可以这样说，卷积层 a 中的一个权值在减少错误方面的平均效果是全连接层 B 中的平均权值的 1/3，反之亦然。这种方法使我们能够有效地重新分配权重：如果我们发现了“无用的”权重，我们现在就可以精确地知道应该把它们放在哪个层中 — 但是应该把它们放在一个层的什么地方呢?

什么样的权值应该去掉？在什么地方重新把这个权值长出来？

接下来的两个问题比较简单：哪些是最没用的权重？我们如何在一层中增加权重？第一个问题是神经网络压缩研究中的一个常见问题，在这个问题中，我们经常删除具有最小幅值的权值。为什么会这样呢？如果我们假设所有的权值都接收到相同大小的平均输入— 如果使用批处理归一化的话，这是一个合理的假设 — 那么较小的权值对神经元激活的影响最小。因此，删除它们应该会对我们的网络的预测性能产生最小的影响。

一旦我们删除了权值并将它们重新分配到权值有效的层中(通过一层的平均动量大小来测量)，我们就需要决定在一层中到底在哪里生长它们。如果我们问：“如果我们把两个未连接的神经元连接起来，哪两个神经元会持续地减少误差？”这个问题的答案将再次指向动量大小。然而，这一次，我们想看看“缺失”或零值权值的动量大小，也就是说，我们想看看那些以前被排除在训练之外的权值。因此，我们在缺失权值的动量最大的位置增加权值。这样就完成了稀疏动量算法，如图 1 所示。

结果

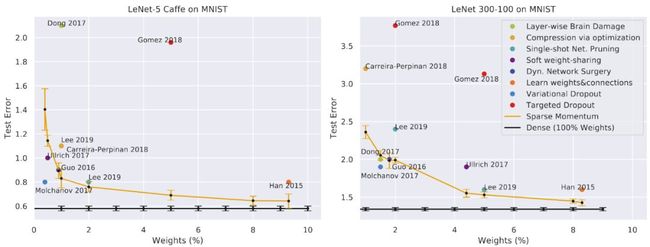
结果令人印象深刻！我们比较了 MNIST 上的压缩算法，其中稀疏动量优于大多数其他方法。这是一个非常好的结果，因为压缩方法是从一个密集的网络开始的，并且通常在我们从零开始训练稀疏网络时需要重复地进行再训练！另一个令人印象深刻的结果是，通过使用 20%的权重(80%的稀疏性)，我们可以匹配甚至超过密集网络的性能。在 CIFAR-10 上，我们将其与单次修剪的网络进行了比较，后者的设计是为了简单而不是性能 — 因此，稀疏动量做得更好并不奇怪。然而，有趣的是，我们可以同时训练 VGG16-d (VGG16 的一个版本，具有两个全连接的层)和 Wide Residual Network(WRN)16-10(16 层深和非常宽的 WRN)，只使用了 5%的权值就使其达到了密集网络的性能级别。对于其他网络，稀疏的动量接近于密集网络的性能水平。此外，正如我将在后面展示的，通过一个优化的稀疏卷积算法，我们将能够训练多种网络来产生相同的性能水平，而训练速度在 3.0-5.6 倍之间！

LeNet-300-100和LeNet-5caffe在MNIST上的稀疏动量结果与神经网络压缩方法的比较

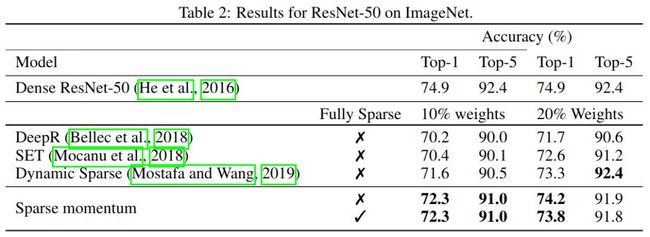
稀疏动量的ImageNet结果及相关方法。对于非完全稀疏的模型，从训练开始，第一次卷积和所有下采样剩余连接都是密集的。在完全稀疏的情况下，所有层都是稀疏的。稀疏动量比其他方法更有效，如果所有的权值都是稀疏的，其效果几乎是一样的。这表明稀疏动量在寻找需要高密度的重要层时是有效的。

在 ImageNet 上，我们无法达到密集网络的性能级别，这表明有改进稀疏动量的空间。然而，我们可以证明，与其他在训练过程中保持稀疏权值的方法相比，稀疏动量具有明显的优势。

加速

稀疏学习的主要承诺是加速训练——我们成功了吗？是也不是。如果我们测量稀疏卷积可能的加速，那么稀疏动量可以有效地加速训练，但是因为稀疏网络只是最近才被用于训练，所以对于 GPU 来说没有优化的稀疏卷积算法存在——至少对于稀疏动量所展示的细粒度的稀疏权值模式不存在。

因此，我们将加速分为两组：一组是在存在稀疏卷积算法的情况下可能实现的加速，另一组是在标准的密集卷积算法下可以实现的加速。稠密卷积如何帮助稀疏网络？

如果我们观察网络的稀疏模式，我们会发现卷积通道是完全空的 — 卷积滤波器充满了 0 ！如果发生这种情况，我们可以在不改变卷积结果的情况下从计算中移除通道，从而获得加速。

稀疏动量可以在一系列网络中复制密集网络的性能水平，从而导致加速。

然而，如果我们看一下加速，我们会发现在稀疏卷积和稠密卷积加速之间有一个明显的区别。这清楚地说明了 GPU 对优化的稀疏卷积算法的需求。

为什么稀疏学习可以工作？

我们的一些用稀疏动量训练的稀疏网络与只有 5%权值的密集网络的性能水平相匹配。是什么让这 5%的权重如此高效，以至于它们可以与一个权重是它 20 倍的神经网络相匹配？

为了研究这个问题，我们研究了稀疏网络和稠密网络的特征。低级特征可能包括边缘检测器之类的东西。中等水平的特征可能是轮子、鼻子、眼睛、爪子等。高级特征可能是汽车的“脸”、猫的脸、冰箱门等等。

为了将特征简化为数字，我们考虑了卷积通道——相当于卷积网络中的一个“神经元”——以及该通道对数据集中的类有多有用。边缘检测器应该对数据集中的几乎所有类都有用——换句话说，它们应该是不区分特定类别的。中等水平的特征，如眼睛，对猫、狗和人等类别是有用的。高级特征应该对一些特定类有用 —— 它们是高度类别化的。

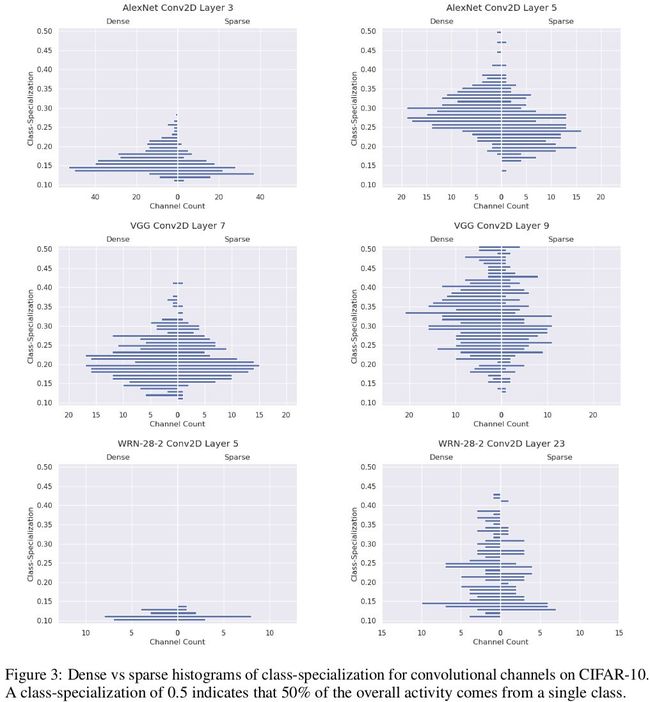
AlexNet, VGG16和wrn28 -2上稀疏和稠密网络的类别化的直方图

我们发现，平均而言，稀疏网络学到的是对更大范围的类有用的特征——它们学习更一般的特征。这也许可以解释为什么稀疏网络的性能可以与只有 5%权值的稠密网络相匹配。

稀疏学习的特征

我相信稀疏学习有一个非常光明的未来，因为(1)gpu 的性能在未来几年将停滞不前，(2)用于稀疏计算的专用处理器，Graphcore 处理器，即将出现。Graphcore 处理器将整个网络存储在其 300MB 的缓存中，并将其加速约 100 倍。这意味着，如果我们可以在训练时将网络压缩到 300MB，那么我们的训练速度将提高 100 倍。使用一个 Graphcore 处理器，在 ImageNet 上训练一个 ResNet-50 只需要大约 15 分钟。通过稀疏学习，300 MB 的限制将不会出现问题。

我的预测是，第一个能够在 Graphcore 处理器上成功训练稀疏神经网络的研究团队将开启人工智能的一个全新水平。

除此之外，另一个挑战是将稀疏学习算法应用于自然语言处理(NLP)。毫不奇怪，我在自然语言处理任务的 transformers 上的实验表明，与计算机视觉相比，在 NLP 中进行稀疏学习要困难得多——有大量的工作要做！

使用 10 行代码在你自己的模型上尝试稀疏动量！

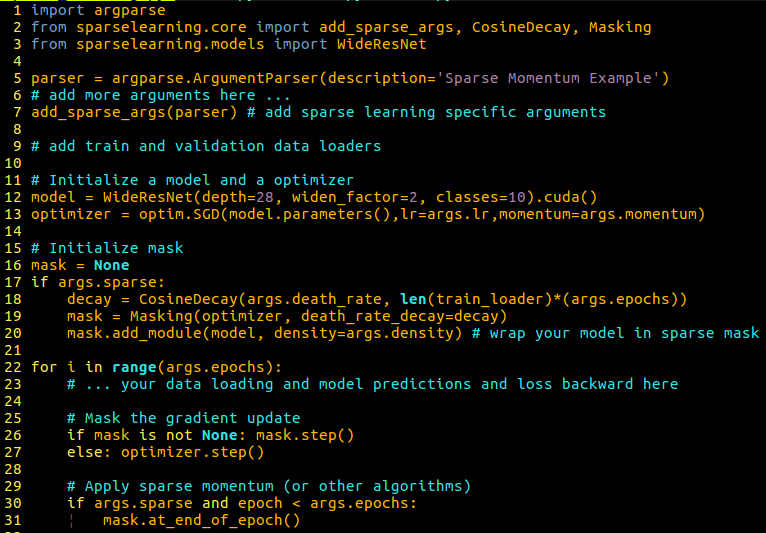
一个通用的稀疏学习脚本的例子，可以用于拟自己的模型。在我的sparselearning库中，使用稀疏动量很容易：(1)导入这个库，(2)添加解析器选项，(3)用屏蔽类包装模型，(4)应用掩码而不是优化器，(5)在epoch结束时应用稀疏动量。使用你自己的稀疏学习算法(用于增长、修剪或重新分配)，这个库也很容易扩展—只需几行代码！

为了使每个人都能使用稀疏学习，我开发了一个稀疏学习库，它允许将现有的算法(如稀疏动量)轻松应用到你自己的模型中——这可以在不到 10 行代码中完成。这个库还可以让你很容易地添加自己的稀疏学习方法。你可以在 GitHub 上找到我的稀疏学习库^[2]

参考资料

[1]

Sparse Networks from Scratch: Faster Training without Losing Performance: https://arxiv.org/abs/1907.04840

[2]

稀疏学习库: https://github.com/TimDettmers/sparse_learning

—END—

英文原文：https://timdettmers.com/2019/07/11/sparse-networks-from-scratch/

请长按或扫描二维码关注本公众号

喜欢的话，请给我个好看吧！