模型压缩:Deep Compression
-
- 第一步weight pruning
- 第二步trained quantization and weight sharing
- 第三步 Huffman coding
- 实验分析之压缩几十倍从何而来
- 实验分析之极致量化
《Deep Compression Compressing Deep Neural Networks with Pruning, Trained Quantization and Huffman coding》是ICLR-2016的 best paper,斯坦福的由HanSong等人共同发表。
arXiv(发音: 美[ˈɑ:rkaɪv]) :https://arxiv.org/abs/1510.00149
前言:
从文章标题就知道,这是一篇关于模型压缩的论文,整体步骤分为三部:pruning ,quantization, coding。也就是,剪枝、量化、编码。熟悉通信理论的同学,对量化、编码再熟悉不过了,因此,针对于网络模型的操作仅仅体现在pruning上,而之后的量化和编码,可以归为信息存储技术。
模型压缩最终的目的不外就两个:
1. 存储问题 ,在不怎么损失网络性能的前提下,尽可能的占用更少的内存,以至于可以部署在移动端;
2. 速度问题 ,在不怎么损失网络性能的前提下,尽可能的提高inference时的速度,以达到实时处理。
然而,本文提出的方法,仅仅针对问题1.存储问题 !对于inference的速度,并没得到什么提升,原文1.introduction中有一句话单独设为一段:
“Our goal is to reduce the storage and energy required to run inference on such large networks so they can be deployed on mobile devices.”
正文:
讲解deep compression的步骤,以及实验结果以及结论。
第一步:weight pruning
整个Pruning分三小步:
step1. 正常的训练网络,得到压缩之前的pre-train model
step2. 真正意义的pruning:对权值设定一个阈值,小于阈值的权值就被置 0
step3. 重新训练经过pruning之后的网络
pruning的方法是对权值设置一个阈值,小于阈值的权值就“移除”,简单除暴。但是如何设置这个阈值呢?本文中并没有介绍,因为这个方法是引用另外一篇论文(同样是HanSong老师的论文)—— 《Learning both weights and connections for efficient neural networks》
因此,在研读完本文之后,非常有必要去拜读这篇论文。
经过权值剪枝,网络就是一个稀疏结构的网络了,因为有很多权值小于设定的阈值,被置为“0”了嘛。而针对稀疏结构,CSR (compressed sparse row) or CSC(compressed sparse column )是非常高效的存储方式。因此,对权值剪枝之后的模型,就采用CSR的方式来存储。
CSR简介(截取自:http://blog.csdn.net/may0324/article/details/52935869):
假设有一个原始稀疏矩阵A

CSR可以将原始矩阵表达为三部分,即AA,JA,IC
其中,
AA中的元素值 代表 矩阵A中所有非零元素值;
JA中的元素值表示的是序号,是矩阵A中每行第一个非零元素在AA中的位置序号(即AA中红框标出来的元素的序号)。而A有五行,JA却有6个元素,可以发现最后一个元素值是 14,其实就是A中非零元素个数(13)+1 ;
IC是AA中每个元素对应的列号,长度为a=13。
注:a表示A矩阵非零元素个数,n表示矩阵行数。
所以将一个稀疏矩阵转为CSR表示,需要的空间为2*a+(n+1)个 ,同理CSC也是类似。
第二步:trained quantization and weight sharing
量化,即一个数用几个bit来表示,用的bit数越大,占的内存越多,精度也就越高,但是到底需要多少bit就可达到我们所需的网络性能呢?依据实验结果是6~8bit。
weight sharing,即是将同一层当中所有的权值进行聚类(K-means聚类),属于同一类的那些权值全部使用该类的聚类中心作为权值。通过weight sharing,只需要存储聚类中心,以及Index,即每个权值对应属于哪个类。因此经过权值压缩比率为:

其中N为该层的连接数,也就是权值数量,b表示使用的bit数;
Nlog2(K)表示存储所有Index所占bit数,Kb表示存储聚类中心所需的bit数,K即表示要聚为多少类。
在这里,K的选取需要通过实验来确定,在本文实验,AlexNet的卷积层中,K=256,即一个Index需要log2(256)=8 bit 来存储,在全连接层中,K=32,一个Index需要占用5 bit
经过量化和weight sharing之后,需要对网络再进行fine-tune,fine-tune时,权值的更新是针对聚类中心进行更新,具体公式为:
其中,Iij表示Wij所属聚类中心的Index,Ck表示第k个聚类中心。对一个聚类中心进行更新的值即对该类内的权值的梯度进行求和。
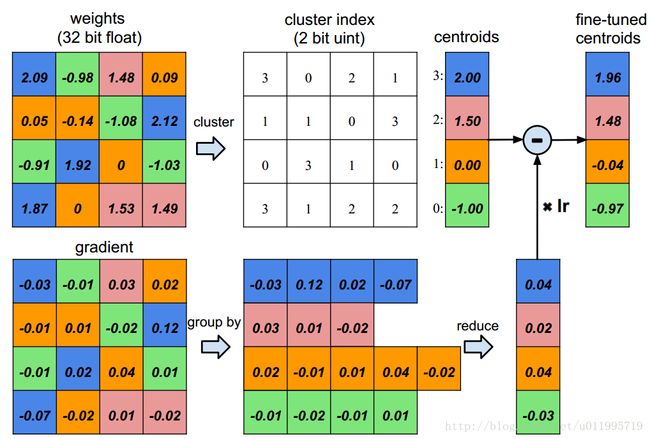
下面举例说明量化,weight sharing, 权值更新 这三个步骤。
假设有一层4个input,4个output的全连接层,并且每个权值占32 bit,则该层权值如下:
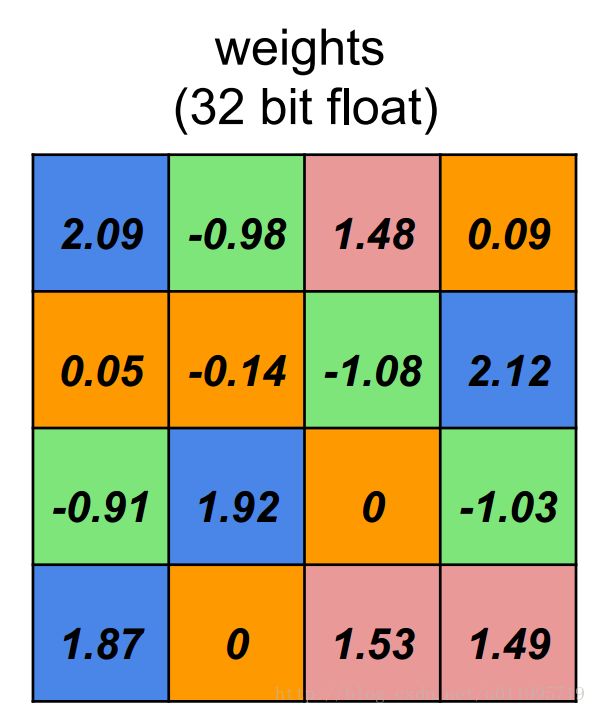
第一步,量化,这里假设仍旧采取32bit来存储一个权值
**第二步,weight sharing。**weight sharing的第一步就是先聚类,这里设K=4,也就是聚为4类,可得:

原本对每个权值需要占用32bit,经过聚类之后,每个权值只需要记录所属哪一个聚类中心即可,因为K=4,因此每个index需要 lob2(4) =2 bit; 由于仍旧采取32bit来存储权值,则右边的centroids(聚类中心) 共需要 4*32 = 128bit来存储。
则经过量化和weight sharing,压缩比率为: 16 32 / (16 log2(4) + 16 *32 ) = 3.2倍
经过了量化和weight sharing,就需要对网络fine-tune了,前面说到,对权值的更新是针对centroids更新,而所需要更新的值,是对属于该centroids的权值的梯度的求和。具体如下:
以index=3(蓝色)为例,index=3的权值分别是2.09、2.12、1.92、1.87,这四个权值对应的梯度为-0.03、0.12、0.02、-0.07,对这四个梯度求和得 -0.03+0.12+0.02-0.07 = 0.04,再将0.04乘以学习率,从而得到 聚类中心index=3的修改值,则fine-tuned centroids 为1.96
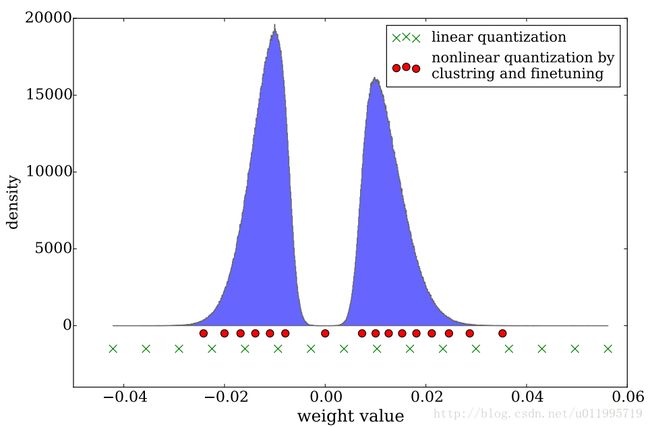
这里还有一个问题就是,如何对聚类中心进行初始化?文假设了三种初始化方法,并且进行实验,最终敲定,采用Linear的方法对聚类中心初始化, 另外两种初始化方法分别是Forgy(随机)和Density-based(基于概率)。为什么选用Linear?
因为两点:
1.权值分布的特点;
2. 较大的权值具有较大的影响力。
先看看权值分布的特点,权值分布可以看到是服从高斯分布的
从图可知,较大的权值所占的比例是较小的,然而较大的权值具有较大的影响力,若采用Forgy或Density-based,都无法确保 大权值 保留有一定的比例。因此采用Linear方法进行初始化。
第三步: Huffman coding
哈夫曼编码就属于信息论里面的内容了,哈夫曼编码就是依据字符出现概率来编码。
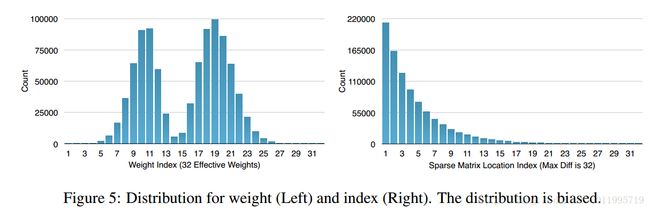
下图为Alexnet全连接层 权值的分布 以及 偏置的分布:
实验分析之压缩几十倍从何而来?
最后来分析一下模型压缩的结果,看看到底怎么把Alexnet压缩了35倍,怎么对VGG-16压缩了49倍的。
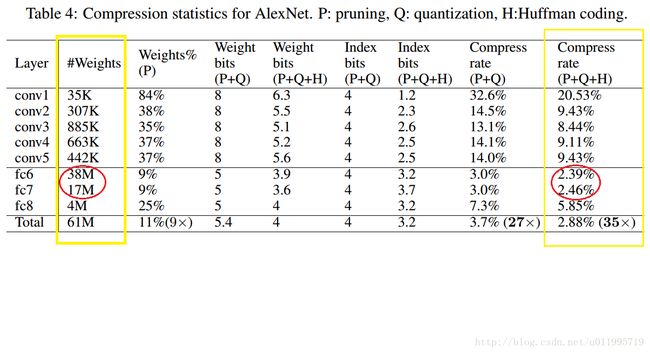
先看左边黄色框,表示各层权值的数量,右边黄色框,是经过P+Q+H后,所剩下参数所占的存储空间!
注意了,左边的是权值数量,右边表示存储空间。
原始总计61M参数,一个权值采用32bit=4B,则共计占61M*4B =244MB 字节 ,经过P+Q+H之后剩下 244MB* 2.88% = 7.0272MB,这个数才是论文开篇描述的 240MB压缩至6.9MB;
现在来看看压缩掉的236.9728MB存储空间当中,全连接层贡献了多少。

全连接层共计压缩存储空间为: 148.3672 + 66.3272 +15.064 = 229.7584 MB
占总压缩存储空间的比例为:229.7584 / (244-7.0272) ≈ 96.96%
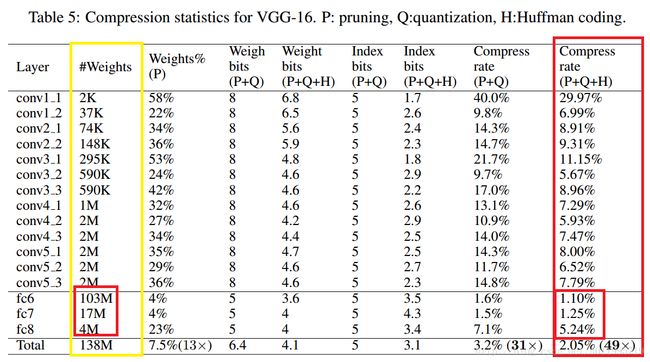
再看看VGG-16
原模型共计占内存 138M * 4B = 552MB, 压缩的存储空间为: 552 * (1- 2.05%) = 540.684
全连接层共计压缩存储空间为: 407.468 + 67.15 + 15.1616 = 489.7796 MB
占总压缩存储空间的比例为:489.7796 / 540.684 ≈ 90.58%
不论AlexNet还是VGG-16,都是含有三个全连接层,尤其是FC6,均占了总参数量的61% 以上,因此模型压缩的倍数如此客观,也是有原因的,毕竟 FC6 FC7太“臃肿”了!
也正因为全连接的问题,虽然模型压缩了几十倍,但是速度几乎没有得到改善。
因此要提升inference速度,还是要在卷积层上面下功夫啊。
实验分析之极致量化
一个权值到底应该量化至何种程度呢? 本文就conv layer及 fc layer 分别进行了 1bit 至 8bit的实验,实验结果如下:
从图中可发现,不论是conv layer 还是 fc layer,低于4bit,性能会迅速下降;
本文最终对conv layer 采用8bit进行编码, fc layer采用5bit;
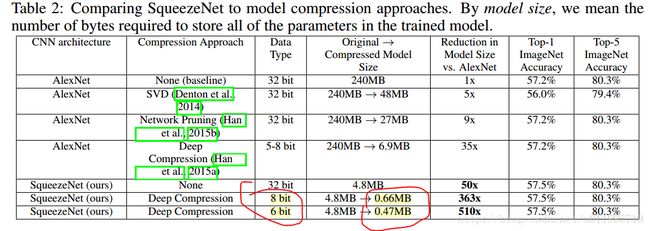
这里有个小插曲,熟悉SqueezeNet的朋友,肯定被它论文标题给惊住了,
《SqueezeNet: AlexNet-level accuracy with 50x fewer parameters and <0.5MB model size
》
< 0.5MB, 论文一出,可是够吸引眼球的。不过这个论文题目是V4版,再V1版当中,可不是<0.5MB的,而是 <1MB:
《SqueezeNet: AlexNet-level accuracy with 50x fewer parameters and <1MB model size
》
原来就是在编码长度上下了功夫~ 从8bit缩减到6bit~~~
小结:
- deep compression是解决存储问题,对于速度问题几乎没获得改善;
- 权值剪枝还得看另外一篇论文:learning both weights and connection for efficient neural network
- 存储空间问题,主要还是在全连接层,若要改善inference速度,需要在卷积层下功夫