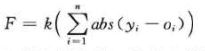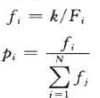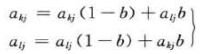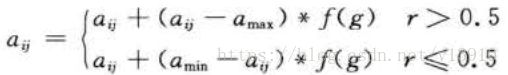遗传算法优化BP神经网络拟合非线性函数
1.遗传算法理论基础
第一次接触遗传算法,觉得这个算法很是神奇啊!遗传算法模拟自然界中“优胜劣汰,适者生存”的法则,形成了一种随机搜索最优化方法。本文主要是讲遗传算法用于优化BP算法,BP算法在拟合非线性函数时,虽然可以收敛,但是有可能收敛到局部最小点,这是源于它的搜索是串行搜索,而遗传算法的并行性,能够使其更容易收敛到全局最小点。在训练神经网络时,目的就是通过不断的优化每一层的权值和偏置值,使最终网络输出与期望输出之间的误差小到我们所期望的值,而这个优化的过程,就是权值和偏置值不断“进化”的过程,在每一次迭代过程中,权值与偏置值由于“自然环境”发生选择,突变,交叉,然后留下优的品种(权值和偏置值使输出误差最小),淘汰劣的品种,进而经过多次迭代,权值与偏置值的“基因”会越来越好,从而达到训练目的。下面介绍几个概念:
1.种群:一个种群中有许多个体,个体之间有差异,有的个体携带的权值和偏置值误差小,有的个体携带的误差大。进化过程以种群为基本单位。
2.编码:就是个体携带的基因型,在BP网络中就是权值和偏置值。
3.适应性:个体优劣程度,在BP网络中,误差大的适应性差,误差小的适应性好。
4.选择:以一定概率在种群中选取若干个体,模拟优胜劣汰过程。
5.交叉:两个个体的编码“基因重组”。
6.变异:个体编码“基因突变”。
遗传算法的进化过程如何实现呢?
1.物种初始化
个体编码携带各层权值与偏置值,种群规模自定义。
2.适应性值
每一个个体都有独特的权值与偏置值,把该个体网络输出与期望输出之间的误差作为个体的适应性。
3.选择
轮盘赌选择法:
f是适应性值的倒数,f越小,适应性越差,p是每个个体被选中的概率,f越大,适应性值越好,被选中的概率也就越大。注意:所有个体概率相加为1,这对理解轮盘赌选择法很重要。
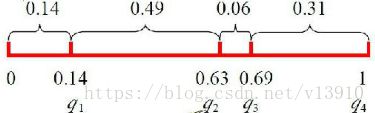
如上图,每一个个体都有被选中的概率,概率和为1。随机产生0~1之间的一个数字x,落在上图哪个区间,哪个个体就被选中,因为0~1数字是随机产生,所以落在区间大的区域的概率更大,区域概率大代表什么?代表这个个体适应性好,好的个体被多次选中,自然“基因”就好了。
4.交叉
选中的优秀个体,组成了新的种群,新种群之间的“杂交”是必要的,可以产生更优秀的“基因”。随机选中两个个体的两个“基因”进行“杂交”(相同段基因)。
5.变异
生物进化只有“杂交”是不行的,有时候需要“基因突变”。
r是0~1之间的随机数,g是当前迭代次数,Gmax是最大迭代次数。
2.具体编程实现Matlab
main.m
clc,clear,close all
%%
%导入数据
data = load('data.mat');
input_data = (data.input)';
output_data = data.output;
%训练使用数据
input_data_tr = input_data(:,1:1900);
output_data_tr = output_data(:,1:1900);
%测试使用数据
input_data_te = input_data(:,1901:2000);
output_data_te = output_data(:,1901:2000);
%训练数据归一化
[input_tr,p] = mapminmax(input_data_tr);
[output_tr,q] = mapminmax(output_data_tr);
%%
%生成网络
input_number = 2;
hide_number = 5;
output_number = 1;
net = newff(input_tr,output_tr,5);
%%
%遗传算法
%定义参数
size = 10;%种群规模 10
time = 50;%迭代次数
pcross = 0.4;%交叉概率
pvariation = 0.2;%变异概率
l = hide_number*input_number+output_number*hide_number+hide_number+output_number;%编码长度
%定义种群结构体
individuals = struct('fitness',zeros(1,size),'chorm',[]);%chorm编码信息 fitness适应度
%初始化种群
lenchrom = ones(1,l);
bound = [-3*ones(l,1) 3*ones(l,1)];
for i = 1:size
individuals.chorm(i,:) = Code(lenchrom,bound);
x = individuals.chorm(i,:);
individuals.fitness(1,i) = fitness_fun(x,input_number,hide_number,output_number,net,input_tr,output_tr);
end
best_fitness = 10;%最优个体适应度
best_chorm = zeros(1,l);%最优个体染色体编码
trace = zeros(1,time);
b = [];
%进化
for i = 1:time
i
%择优
individuals = Select(individuals,size);
%交叉
individuals = Cross(size,individuals,pcross,l);
%变异
individuals = Variation(size,pvariation,l,i,time,individuals,3,-3);
%进化之后的适应度
for j = 1:size
x = individuals.chorm(j,:);
individuals.fitness(1,j) = fitness_fun(x,input_number,hide_number,output_number,net,input_tr,output_tr);
end
%最优个体
[new_best_fitness,index] = min(individuals.fitness);
new_best_chorm = individuals.chorm(index,:);
%最差个体
[worst_fitness,index] = max(individuals.fitness);
if new_best_fitness1.首先导入数据,根据要拟合的非线性函数,得到2000组输入输出数据。其中1900组用于网络训练,100组用于网络测试。训练数据归一化。
2.构造神经网络,输入变量为2,输出变量为1,三层网络结构,设置隐层节点为5。
3.遗传算法优化BP网络训练,定义种群结构体包含编码与适应性值。初始化种群个体的编码(权值和偏置值),计算出适应性值。进化过程:每一次迭代过程,都要进行个体选择,交叉和变异操作。然后计算进化之后的个体适应性值,进行优胜劣汰。
4.迭代完成之后,选取种群中最优的编码作为网络参数,测试数据。
code.m
function ret=Code(lenchrom,bound)
%本函数将变量编码成染色体,用于随机初始化一个种群
% lenchrom input : 染色体长度
% bound input : 变量的取值范围
% ret output: 染色体的编码值
pick=rand(1,length(lenchrom));
ret=bound(:,1)'+(bound(:,2)-bound(:,1))'.*pick; %线性插值,编码结果以实数向量存入ret中
end
fitness_fun.m
function error = fitness_fun(x,input_number,hide_number,output_number,net,input_data,output_data)
%每一个个体都有独立的权值与偏置值组成的编码信息,errer评估当前个体x的适应度
%x 个体
%input_number 输入层节点个数
%hide_number 隐层节点个数
%output_number 输出层节点个数
%net
%input_data 数据输入
%output_data 数据输出
%从个体编码信息中得出权值与偏置值
w1 = x(1,1:input_number*hide_number);
b1 = x(1,input_number*hide_number+1:input_number*hide_number+hide_number);
w2 = x(1,input_number*hide_number+hide_number+1:input_number*hide_number+hide_number+hide_number*output_number);
b2 = x(1,input_number*hide_number+hide_number+hide_number*output_number+1:input_number*hide_number+hide_number+hide_number*output_number+output_number);
net.iw{1,1} = reshape(w1,hide_number,input_number);
net.lw{2,1} = reshape(w2,output_number,hide_number);
net.b{1} = reshape(b1,hide_number,1);
net.b{2} = reshape(b2,output_number,1);
%设置神经网络参数
net.trainparam.epochs = 20;
net.trainparam.lr = 0.1;%learn rate
net.trainparam.goal = 0.00001;
net.trainparam.show = 100;%
net.trainparam.showWindow = 0;%
%训练神经网络
net = train(net,input_data,output_data);
%得出预测值
p_out = sim(net,input_data);
%计算误差作为当前个体的适应度
error = sum(abs(output_data-p_out));
end
Select.m
function ret = Select(individuals,size)
%轮盘赌法
%individuals 种群
%size 规模大小
%个体被选中的概率
k = 10;
f = k./individuals.fitness;%
p = f./sum(f);
%定义优选序列
select_index = zeros(1,size);
for i = 1:size
p_rand = rand;%产生随机数
while(p_rand == 0)
p_rand = rand;
end
for j = 1:size
p_rand = p_rand-p(1,j);
if p_rand<0
select_index(1,i) = j;%第j个被选中
break;
end
end
end
individuals.chorm = individuals.chorm(select_index,:);%
individuals.fitness = individuals.fitness(1,select_index);
ret = individuals;
end
Cross.m
function ret = Cross(size,individuals,pcross,l)
%染色体交叉
for i = 1:size
%随机产生要交叉的两个个体序号
index = rand(1,2);
while prod(index) == 0
index = rand(1,2);
end
index = ceil(index.*size);
%是否交叉?
p = rand;
while p == 0
p = rand;
end
if p>pcross
%选择交叉位置
position = rand;
while position == 0
position = rand;
end
position = ceil(position*l);
%交叉
b = rand;%设置交叉权值
a_adjust = individuals.chorm(index(1,1),position)*(1-b)+individuals.chorm(index(1,2),position)*b;
b_adjust = individuals.chorm(index(1,1),position)*b+individuals.chorm(index(1,2),position)*(1-b);
individuals.chorm(index(1,1),position) = a_adjust;
individuals.chorm(index(1,2),position) = b_adjust;
end
end
ret = individuals;
end
Variation.m
function ret = Variation(size,pvariation,l,g,time,individuals,max,min)
%染色体变异
for i = 1:size
%选择变异的个体
index = rand;
while index == 0;
index = rand;
end
index = ceil(index*size);
%是否变异
p = rand;
while p==0
p = rand;
end
if p>pvariation
%变异位置
position = rand;
while position == 0
position = rand;
end
position = ceil(position*l);
fg = rand*((1-g/time)^2);
pick = rand;
if pick>0.5
individuals.chorm(index,position) = individuals.chorm(index,position)+(individuals.chorm(index,position)-max)*fg;
else
individuals.chorm(index,position) = individuals.chorm(index,position)+(min-individuals.chorm(index,position))*fg;
end
end
end
ret = individuals;
end
测试结果:
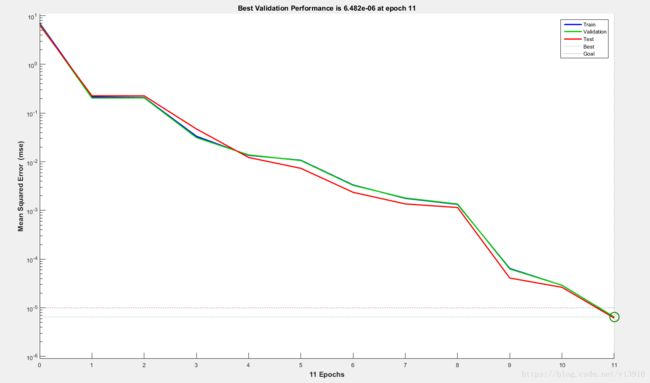
均方误差:
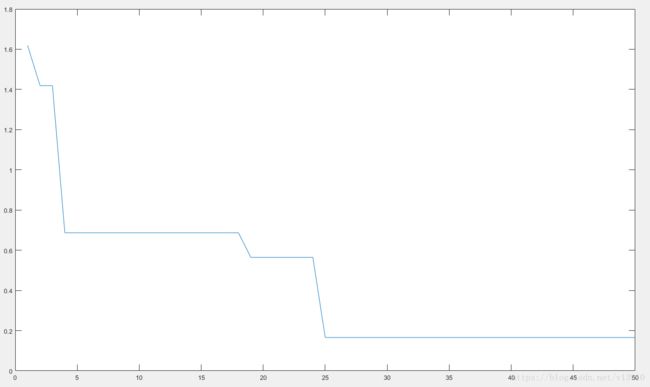
适应性值:
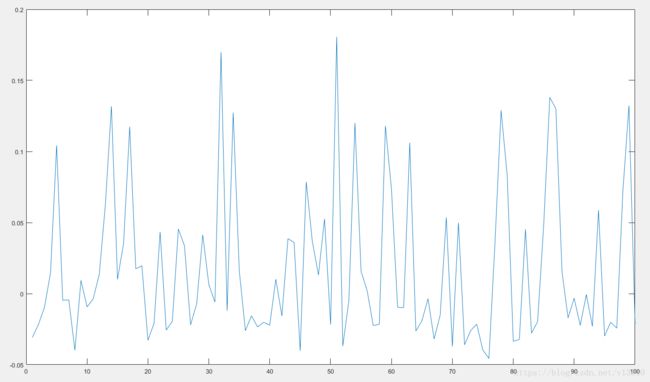
误差: