DeepLearing—CV系列(二十三)——一维卷积或GRU处理电信号、一维卷积、转置卷积的详解
文章目录
- 一、一维卷积
- 1.1 介绍
- 1.2 类别
- 1.2.1 一维Full卷积
- 1.2.2 一维Same卷积
- 1.2.3 一维Valid卷积
- 1.3 具备深度的一维卷积
- 1.4 具备深度的张量与多个卷积核的卷积
- 二、转置卷积
- 2.1 定义
- 2.2 过程
- 2.3 计算
- 2.4 转置卷积的缺点
- 2.5 转置卷积的棋盘效应
- 2.5.1 产生原因
- 2.5.2 解决方案:
- 三、一维卷积应用场景
- 四、转置卷积应用场景
- 五、代码
- 5.1 net.py
- 5.2 sample_train
- 5.3 Train.py
- 5.4 信号拟合效果展示
一、一维卷积
1.1 介绍
1.2 类别
一维卷积通常有三种类型**:full卷积、same卷积和valid卷积**
1.2.1 一维Full卷积
Full卷积的计算过程是:K沿着I顺序移动,每移动到一个固定位置,对应位置的值相乘再求和,计算过程如下:

将得到的值依次存入一维张量Cfull,该张量就是I和卷积核K的full卷积结果,其中K卷积核或者滤波器或者卷积掩码,卷积符号用符号★表示,记Cfull=I★K

1.2.2 一维Same卷积

卷积核K都有一个锚点,然后将锚点顺序移动到张量I的每一个位置处,对应位置相乘再求和,计算过程如下:


假设卷积核的长度为FL,如果FL为奇数,锚点位置在(FL-1)/2处;如果FL为偶数,锚点位置在(FL-2)/2处。
1.2.3 一维Valid卷积
从full卷积的计算过程可知,如果K靠近I,就会有部分延伸到I之外,valid卷积只考虑I能完全覆盖K的情况,即K在I的内部移动的情况,计算过程如下:


1.3 具备深度的一维卷积
比如x是一个长度为3,深度为3的张量,其same卷积过程如下,卷积核K的锚点在张量x范围内依次移动,输入张量的深度和卷积核的深度是相等的。

1.4 具备深度的张量与多个卷积核的卷积
上面介绍了一个张量和一个卷积核进行卷积。他们的深度相等才能进行卷积,下面介绍一个张量与多个卷积核的卷积。同一个张量与多个卷积核的卷积本质上是该张量分别与每一个卷积核卷积,然后将每一个卷积结果在深度方向上连接起来。
举例:以长度为3、深度为3的输入张量与2个长度为2、深度为3的卷积核卷积为例,过程如下:

二、转置卷积
2.1 定义
之所以叫转置卷积是因为,它其实是把我们平时所用普通卷积操作中的卷积核做一个转置,然后把普通卷积的输出作为转置卷积的输入。而转置卷积的输出,就是普通卷积的输入。
卷积操作的本质其实就是在input矩阵和kernel矩阵之间做逐元素(element-wise)的乘法然后求和。
根据反卷积的数学含义,通过反卷积可以将通过卷积的输出信号,完全还原输入信号。转置卷积只能还原shape大小,而不能还原value(愿意:神经网络是基于概率;反向传播损失不会等于0,只能与真实值接近)。所以说转置卷积与真正的反卷积有点相似,因为两者产生了相同的空间分辨率。
转置卷积的过程中图像上采样,越来越大,通道越来越浅。需要注意的是,转置前后padding,stride仍然是卷积过程指定的数值,不会改变。
转置卷积一般会放大图像,也称为上采样过程,而卷积一般是缩小图像,也称为下采样过程。
2.2 过程

卷积操作是多对一(many-to-one)的映射关系。

转置卷积是多对一(one-to-many)的映射关系
2.3 计算
步长=1时,外圈padding=k-1
步长>1时,外圈padding-k-1,内圈out_padding=s-1
转置卷积后的特征图计算公式:s*(N-1)+k-2p

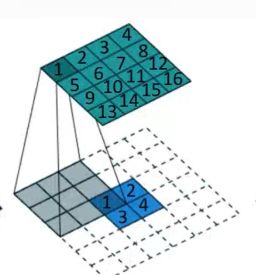
2.4 转置卷积的缺点
(1)卷积矩阵是稀疏的,因此大量的信息是无用的;
(2)求卷积矩阵的转置矩阵是非常耗费计算资源的。
2.5 转置卷积的棋盘效应
当我们要用到深度学习来生成图像的时候,是往往是基于一个低分辨率且具有高层语义的图像。这会使得深度学习来对这种低分辨率图像进行填充细节。一般来说,为了执行从低分辨率图像到高分辨率图像之间的转换,我们往往要进行deconvolution。简单来说,deconvolution layer可以允许模型通过每一个点进行绘制高分辨率图像上的一个方块,这种情况的产生与deconvolution的stride、kernel size有关。
转置卷积会在生成的图像中造成棋盘效应(checkerboard artifacts).本文推荐在使用转置卷积进行上采样操作之后再过一个普通的卷积来减轻此类问题.
2.5.1 产生原因
kernel size无法被stride整除
stride为1,kernel size为3,这导致了重复上采样绘图的部分不均匀(下图深色部分),

二维情况更为严重,

2.5.2 解决方案:
思路一:确保反卷积核的大小可以被步长整除,从而避免重叠问题
(1)多层重复转置卷积:
一个常见的想法是寄希望于多层重复转置卷积,希望能抵消掉棋盘效应,但是实际上一般事与愿违,重复的结构使得棋盘更加复杂。

(2)网络末尾使用1x1的反卷积,可以稍微抑制棋盘效应

(3)调整kernel权重分布:
加大无重叠部分的权重分布可以很好的解决的这个问题,原理如下图:

但是这种做法会极大地限制模型的学习能力(避免棋盘效应往往会降低模型容量,会使得模型变得更大从而使得难以训练。原文的话是指: Avoiding artifacts significantly restricts the possible filters, sacrificing model capacity)
(4)采取可以被stride整除的kernel size
该方案较好的应对了棋盘效应问题,但是仍不够圆满,因为一旦我们的kernel学习不均匀,仍然会产生棋盘效应,

在上图中,我们的weight并不够平衡,这直接导致了输出的棋盘效应。
即便如此,采用这个思路去设计网络仍然是必要的。
思路二:更好的上采样(将上采样分离为较高分辨率的卷积到计算特征):
(5)插值
可以直接进行插值resize(使用最近邻插值或双线性插值)操作,然后再进行卷积操作。这种操作在超分辨率文献中很常见。例如,我们可以采取近邻插值或者样条插值来进行上采样。

三、一维卷积应用场景
众所周知,一维卷积常用来处理序列模型,通过训练好的一维卷积模型可以在前面数据的基础上预测下一时刻的信号。在这里,我用一维卷积处理了两地之间电力传输的信号,通过训练好的模型可以有效预测下一时刻的电信号,从而判断当前信号是否符合标准。
四、转置卷积应用场景
对于上采用的需求
(1)当我们用神经网络生成图片的时候,经常需要将一些低分辨率的图片转换为高分辨率的图片。
(2)在DCGAN中的生成器将会用随机值转变为一个全尺寸(full-size)的图片,这个时候就需要用到转置卷积。
(3)在语义分割中,会使用卷积层在编码器中进行特征提取,然后在解码层中进行恢复为原先的尺寸,这样才可以对原来图像的每个像素都进行分类。这个过程同样需要用到转置卷积。
五、代码
5.1 net.py
一维卷积模型
import torch.nn as nn
class Net(nn.Module):
def __init__(self):
super(Net,self).__init__()
self.conv1 = nn.Sequential(
nn.Conv1d(1,32,3,2,1),
nn.BatchNorm1d(32),
nn.ReLU()#5
)
self.conv2 = nn.Sequential(
nn.Conv1d(32,64,3,2,1),
nn.BatchNorm1d(64),
nn.ReLU()#3
)
self.conv3 = nn.Sequential(
nn.Conv1d(64,128,3,1,0),
# nn.BatchNorm1d(128),
nn.ReLU()#1
)
self.fc = nn.Sequential(
nn.Linear(128,1),
nn.Sigmoid()#1
)
def forward(self, x):
y1 = self.conv1(x)
y2 = self.conv2(y1)
y3 = self.conv3(y2)
y3 = y3.reshape(-1,128)
y4 = self.fc(y3)
return y4
GRU(循环神经网络,LSTM的变体)
class rnn_net(nn.Module):
def __init__(self):
super().__init__()
self.lstm = nn.GRU(
input_size=9,
hidden_size=128,
num_layers=1,
batch_first=True,
bidirectional=True
)
self.out = nn.Linear(128 *2, 1)
def forward(self, x):
y, (c_s, h_s) = self.lstm(x, None)
# print(y.shape)
# print(c_s.shape)
# print(h_s.shape)
out = self.out(y[:, -1, :])
# print(out.shape)
return out
5.2 sample_train
import random
import numpy as np
import torch
def Get_data():
data = torch.randint(10, 100, (100,), dtype=torch.float32)
data2 = torch.randint(-3, 3, (100,), dtype=torch.float32)
test_data = data + data2
return test_data
5.3 Train.py
训练时我用长度为9的一维信号输入网络得到一个长度为1的信号,再将它与标签信号做损失在优化
import torch
import torch.nn as nn
import numpy as np
import sample_train
import net
import matplotlib.pyplot as plt
import os
if __name__=="__main__":
epohs = 1000
net = net.Net().cuda()
save_path = r"params/1dnet.pth"
opt = torch.optim.Adam(net.parameters())
loss_fn = nn.BCELoss()
get_data = sample_train.Get_data()
max_data = float(torch.max(get_data))
data = np.array(get_data) / max_data
if os.path.exists(save_path):
net.load_state_dict(torch.load(save_path))
else:
print("NO Param")
for epoh in range(epohs):
a=[]
b=[]
c=[]
for i in range(0,len(data)-9):
x = data[i:i+9]
# print(x)
y = torch.tensor(data[i+9:i+10],dtype=torch.float32).cuda()
xs = torch.tensor(x.reshape(-1,1,9),dtype=torch.float32).cuda()
out = net(xs)
output=out[0]
loss = loss_fn(output,y)
opt.zero_grad()
loss.backward()
opt.step()
a.append(i)
b.append(out.item())
c.append(y.item())
plt.plot(a,b,"red",label="data")
plt.plot(a,c,"blue",label="label")
plt.legend(loc="upper left")
plt.pause(0.01)
plt.clf()
print("epoh:{} loss:{}".format(epoh,loss.item()))
# torch.save(net.state_dict(),save_path)
plt.savefig("img/{}-figure".format(epoh))




