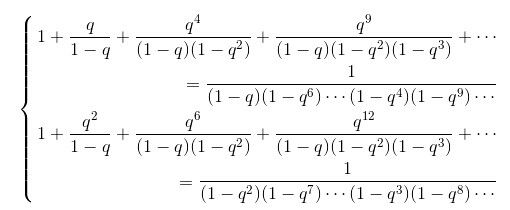印度数学家拉马努金
(这篇文章出自《数学家思想文库 一个数学家的辩白》,我做了一些校对和修正。)
本文系哈代于1936年8月31日在哈佛文学和科学三百年纪念大会上发表的演讲。详见本文末的注释。
在这些演讲中我赋予自己一项真正困难的使命,如果我打算一开始就提出种种失败的理由,那我就会说这个使命几乎是不可能完成的。我必须亲自,并尽力帮助你们,对近代数学史上这位最浪漫的人物做出某种理智的评价,而我从未真正做出过这种评价;这个人的一生充满了矛盾和争议,他违反几乎一切我们常用来评判他人的原则,所有人对他的评价,大概只有一点是一致的,那就是,在某种意义上,他是一位非常伟大的数学家。
评价拉马努金的困难之处显而易见,十分艰难。拉马努金是印度人,我想,一个英国人和一个印度人要彻底相互理解总会有困难。他充其量只是半受教育的印度人;从未在接受正统的印度教育方面胜人一筹,何况这种教育原不足称道。他没能通过印度大学中的“一等文科考试”,甚至从未凑合着当上“不及格的文学士”。他一生中大部分时间都在对现代欧洲数学完全无知的情况下工作,30岁出头就去世了,而这时,某种意义上,他几乎还没开始受到数学教育。他发表的作品很多——论文集有将近400页的一大卷——但还留下了大量未发表的工作,直到近几年才被彻底地分析。这些工作包含许多新东西,但更多的是再发现,而且通常是不完善的再发现。有时候,依然做不到区分哪些结果是他重新发现的,哪些可能是他学来的。甚至今日,我也想象不出有谁能确定无疑地评判,他是一个多么伟大的数学家,更不必说有谁敢肯定地判断,他本可能成为多么伟大的数学家。
这些都是确实无疑的困难,但是我想我们会发现其中有些难处不像看起来那么可怕,而就我来说,最大的困难与拉马努金数学生涯的明显悖谬无关。我的真正困难在于,某种意义上,拉马努金是我的发现。我没有发明他——像一切伟人一样,他发明了自己——但在有幸看到他的某些工作的人中,我是第一个够资格的人。我立刻就看出我发现了一块怎样的瑰宝,至今回想此事,我仍对自己感到非常满意。我想我比任何人都更了解拉马努金,我依然是拉马努金这一特殊课题的首要权威。对于拉马努金的某部分工作,英国还有别的人比我更熟悉,尤其是沃森(Watson)教授和莫德尔(Mordell)教授,但无论沃森还是莫德尔都不像我那样熟悉拉马努金本人。好几年里,我几乎天天见他,同他聊天,最重要的是,我切实地同他合作过。在这个世界上,除了一个人①之外,我得益于他胜过得益于世上其他任何人,同他的交往是我生命中一段浪漫的插曲。我的难处不在对他了解不够,而在于我了解和感受得太多,以至于我就是做不到不偏不倚。
关于拉马努金的生平事迹,我引用耶尔和拉奥,他们写的拉马努金回忆录,同我写的回忆录一起发表在拉马努金的《论文集》中。拉马努金1887年出生于马德拉斯管区坦焦尔(Tanjore)县的一个中型镇——贡伯戈纳姆附近埃罗德的一个婆罗门家庭。他父亲是贡伯戈纳姆一家服装商店的店员,他的亲戚们种姓都很高,但很贫穷。①指J.E.利特尔伍德。——一译注
7岁时他被送到贡伯戈纳姆中学,在那儿读了9年。在10岁之前他的特殊才能就已使他脱颖而出,到12或13岁时,人人都知道他是个天赋异禀的孩子。他的传记作者讲述了他早年一些有趣的故事。例如,他们说,开始学习三角学后不久,他就独立发现了“欧拉正弦和余弦定理”(照我的理解,这是说圆函数和指数函数之间的关系),后来他从龙内的《三角学》第二卷中看到这是一个已知结果时失望之极。直到16岁为止,他从未见过高层次的数学书。那时惠特克(Whittaker)的《现代分析》还没有流传到那么远的地方,布拉米奇的《无穷级数》还没出版。毫无疑问,如果得到这两本书中的任何一本,都将大大改变他的人生之路。然而另一本完全不同类型的书,卡尔的《概要》,最先激发了拉马努金的全部天赋。
卡尔的书(《纯粹和应用数学基本结果概要》,作者G.S.卡尔从前是剑桥冈维尔和凯厄斯学院的学者,该书(1880和1886年出版两卷)现在几乎找不到了。剑桥大学图书馆存有一份复本,恰巧贡伯戈纳姆政府大学图书馆中有一本,拉马努金的一个朋友帮他借到了它。这本书在任何意义上都不是一本出色的书,但拉马努金使它成名,无疑这本书对拉马努金产生了深远的影响,读熟这本书,便是他数学生涯的真正起点。这样的书定然有它自身的品质,纵使卡尔的书不是什么高级的书,但也绝非三流的教科书,而是一本以真正的学者身份和热情写成的、具有自身的风格和特点的书。卡尔本人是伦敦的一位私人教师,大约40岁时来到剑桥做学生,是1880年数学荣誉学位考试第12名(同年他出版了著作的第一卷)。现在除了拉马努金使他名声不朽,已经无人记得他了,甚至在他自己的学院里也是如此。但他定然是一个在某些方面相当出色的人。
我猜想这本书实质上是卡尔辅导笔记的概要。如果你是卡尔的一名学生,学习了《概要》中的适当章节。该书大约包含了现在的数学荣誉学位考试A等级部分的课题(因为这些课题在1880年剑桥大学已为人所理解),并且确实像它自称的那样是个“概要”。它包含了6165条定理的阐述,这些定理系统而十分科学地排列着,附上的证明绝对是这本书中最无聊的部分,通常只比参见书中其他定理稍详细一点儿。所有这些特点在拉马努金著名的笔记本(它实际上完全没有证明)中被放大了,学习笔记本的学生都看得出,拉马努金展示定理的方式完全沿袭自卡尔的书。
卡尔书中有些章节讨论代数,三角学,微积分和解析几何等常见的科目,但不同章节描绘的详尽程度不一样,尤其是积分的形式理论,这似乎是卡尔宠爱的专题,对它的论述非常充分而且讲的特别好。没讲函数论,我非常怀疑拉马努金,直至他生命的尽头,是否完全清楚地弄懂过什么是解析函数。更为令人吃惊的是,考察卡尔本人的兴趣和拉马努金之后的工作,都没有谈及椭圆函数。不管拉马努金怎么获得他关于这一理论的非常奇特的知识,它不是来自卡尔。
总之,作为对于具有如此不寻常天赋的孩子的鼓舞者,卡尔不算太糟,而且拉马努金的反应则令人惊艳。他的印度传记作者①,写道:
在这个向他打开的新世界里,拉马努金兴高采烈地漫游着。正是这本书唤醒了他的天赋,他开始证实书中给出的公式。由于没有其他书的帮助,就他所及,每个解法都是一项研究……拉马努金曾说娜玛 ¥卡(Namakkal)女神在梦中用公式向他启示。有一个令人印象深刻的事实,他经常在起床时记下结果并迅速地证明它们,不过一般不能给出严格证明……
①引文(除那些出自我自己关于拉马努金的回忆录外)出自耶尔和拉奥。——原注
我有意引用最后几句话,不是因为我重视它们——我同你们一样对娜玛¥ 卡女神毫无兴趣——而是因为我们正接近于拉马努金生涯中困难和悲剧性的部分,我们必须尽自己所能去努力理解他的心理状态以及早年笼罩在他周围的气氛。
我肯定拉马努金并不神秘,除在一种严格的物质意义上,宗教在他的生活中并不重要。他是正统的、高种姓的印度人,通常谨守(在住在英国的印度人中,他谨守的严厉程度极为罕见)所有他的种姓的规矩。他曾向父母许诺这样做,并在字面意义上恪守他的诺言。他是最严格的素食者——后来他生病时,这一点使他过的非常困难——他在剑桥的日子里总是自己做饭,而且一定要先换上教徒穿的宽松衣裤再做。
发表在《论文集》上的两篇关于拉马努金的回忆录(都是由在不同侧面对拉马努金很熟悉的人写的)在关于他的宗教信仰方面观点截然相反。耶尔和拉奥写道:
拉马努金有明确的宗教观,他对娜玛¥ 卡女神怀有特殊的崇敬……他相信至高神的存在以及肉身成神……他已树立起关于此世与彼世问题的信念。….
而我写道:
……他的宗教观念不过是对仪式的谨守而非头脑清醒的信念,我清楚地记得他告诉我(令我很吃惊)在他眼里,所有的宗教都或多或少同样真实……
我们谁是对的?对我来说,根本毫无疑虑,我十分自信我是对的。
我相信古典文学学者在文献批评学中有一个基本的校勘原则——difficilior lectio potior ——越难解读的越准确。如果坎特伯雷大主教告诉一个人他信仰上帝,而告诉另一个人他不信,那么第二个阐述更可能是事实,因为若非如此,就无法解释他为什么这么说,而有太多出色的理由可以解释为什么他要作第一个阐述——无论它是否为真。类比一下,如果像拉马努金这样严格的印度教徒告诉我——他确实这么做了——他并没有确定的信仰,那么有100:1的概率,他说的是真实想法。
这个想法不足以让拉马努金伤害他双亲及他的印度朋友的感情。他不是一个理性的无神论者,而是一个严格意义上的“不可知论者”,他认为印度教或其他宗教都没有什么特别的好处或坏处。印度教比起,比方说吧,基督教来,更是一种谨守规矩的宗教,是否有信仰简直无足轻重。如果拉马努金的朋友觉得他接受了这种宗教传统的教义,那么拉马努金没有必要去让他们幻灭,事实上,他实行着十分无害的,可能确有必要的少说真话原则。
关于拉马努金信仰的这个问题本身并不重要,但也不算完全离题,我确实希望尽我所能地着重强调一件事。拉马努金身上难以理解的东西已经够多了,没有必要再误入歧途,捏造神秘感。就我而言,我足够喜欢他、爱慕他,因此我希望以理性主义者的态度来谈论他。我想向你们说清楚,当拉马努金健康舒适地在剑桥生活时,尽管有些古怪,他和这里所有人同样理智,健全,并且以他特有的方式,同样敏锐。我最不想看到你们做的事情就是举起双手承认“他身上有一些超乎理性的事情,古老的东方智慧,不可思议的现象。”我才不相信什么古老的东方智慧,我想介绍给你们的是一个像其他伟人那样有自己小怪癖的人,但却是个可以与人交往的,人们能以与他饮茶交谈,讨论政治和数学为乐的人。总之,我要给你们看的不是来自东方的奇迹,也不是蒙神启示的白痴或心理怪诞的变态,而是一个恰巧成为伟大数学家的理智之人。
直到大约17岁,拉马努金都过的挺好。
1903年12月,他通过马德拉斯大学的入学考试,翌年一月进入贡伯戈纳姆政府大学的初级文科班学习,并获得苏布拉马尼亚姆(Subrahmanyam)奖学金,这一奖学金通常授予精通英语和数学的学生…...
但此后,一系列悲剧发生了。
到那时,他如此专心于数学研究,以致于把所有的课时——无论英语、历史还是生理学——都用于从事数学研究,对班里发生的事漫不经心。过度投入于数学,长期忽视其他学科,致使他未能升入高年级,随后奖学金也中断了。由于失意,也由于朋友的影响,他逃跑去了北边的泰卢固(Telugu)地区,但浪游了一段时间,又返回贡伯戈纳姆,重新进入大学。由于缺课,1905年他没能保证足够的出席率以得到学期证明。1906年,他进入马德拉斯的帕凯亚帕(Pachaiyappa)学院,但因病又回到贡伯戈纳姆。1907年12月,他以个人学生身份参加一等文科考试,没有通过……
直到1912年,除数学之外,拉马努金似乎没有固定的职业。1909年他结婚了,必须找个长期,但由于他不幸的大学经历,找工作非常困难,大约1910年,他找到了比较有影响的印度朋友,拉马斯瓦米· 耶尔和他的两位传记作者。他们尽力帮他找一个过得去的职位,但所有的努力均告失败。1912年,他做了马德拉斯港务局办公室的办事员,年薪大约30英镑,那时,他差不多25岁,18至25岁是数学家一生中至关重要的年龄段,这段时光已经毁了。他的天赋再也没能得到充分发展。
拉马努金此后的生活,无甚可谈。他第一篇有价值的论文发表于1911年,1912年他的超常天分开始为人所理解。值得注意的是,尽管印度人对他很友好,但唯有英国人有能力为他做些实事。斯普林(F.Spring)先生和沃克(G.Walker)先生帮他弄到了特别奖学金,每年60英镑,足以让一个已婚的印度人过得比较舒适。1913年初他写信给我,我与内维尔(Neville)教授克服了重重阻碍,1914年把他带来英国。在这里,整整三年,他毫无间断地活跃工作着,其成果你们可在《论文集》中读到。1917年夏天他得了病,再未真正康复,他仍继续工作,当然只能断断续续地进行,但直到1920年逝世为止,也没有明显的水准下降迹象。1918年初,他成为皇家学会会员,同年稍晚,他成为剑桥大学三一学院研究员(他是第一个同时获得这两个头衔的印度人)。去世前2个月他写了最后一封数学信,主题是“仿-函数",这也正是去年沃森教授向伦敦数学会做的主席演讲的题目。
拉马努金真正的悲剧不是早逝。当然任何伟人过早谢世都是灾难,但30岁以上的数学家通常已比较老,他的死看似悲哀,也许实则不然。阿贝尔死于26岁,纵使他定然本可能为数学增添许多内容,但他似乎难以变得更伟大。拉马努金的悲剧不在于他的夭亡,而是,在那不幸的5年中,他的天赋被引向歧途,受到束缚并在某种程度上被扭曲。
重读16年前我写的关于拉马努金的文字,虽说如今我比当初更了解他的工作,忆念起他也不复那般炽情,但我找不到太多特别想修正的地方。在我如今看来,只有一句话不可原谅。我写道,
关于拉马努金的工作有多重要,该用什么样的标准来评判他,他会给未来的数学带来多大的影响,人们可能会众说纷纭。他的工作缺乏最伟大的工作所特有的简明和必然性;如果它们不那么奇特的话,会更伟大些。然而这些工作有一样闪光点,是不容否认的,即深刻和无可匹敌的独创性。若是他在年轻时更早被抓住和接受数学训练,他可能会成为一个更伟大的数学家,会发现更多全新的,并且,无疑是,更重要的东西。在另一方面,那样他就会变的不再像拉马努金,而更像一位欧洲教授,所失也可能会大于所得。
我坚持以上的观点,只除开最后一句话,它着实是荒谬的感情用事。当贡伯戈纳姆大学将他们曾拥有的一位伟人拒之门外时,他们当然一无所获,而损失却不可弥补。这是我所知道的无能,僵化的教育体制造成损害的最糟糕的例子。他要求得那么少,只要五年里每年给他60英镑,让他与任何有真知灼见并稍微有点想象力的人偶尔能有接触,这世界就会得到又一个最伟大的数学家。
拉马努金给我的信全文重印在《论文集》中,包括大约120条定理的简略叙述,大部分是从他的笔记本中摘录的规范的恒等式。我引用了很有代表性的15条,其中有两条定理(14)和(15),它们与其他定理一样有趣但其中一条是错的,另一条,这么说吧,是误入歧途了。其余的后来都被某些人证实了,尤其是罗杰斯(Rogers)和沃森找到了特别困难的定理(10)一(12)的证明
(1)
(2)
(3)
(4)
(5)
(6)
(7)若,则
(8)
(9)
(10)
若
,
则
(11)
(12)
(13)若且
则
(14)展开后,的系数为最接近的整数
(15)A与x之间的平方数或两平方数之和的个数是
其中与前面的积分相比很小
我希望你们试着想像普通的数学教授收到一位籍籍无名的印度职员这样一封信时的第一反应。
第一个问题是我是否能看出什么东西。我自己证明过颇像(7)那样的公式,对(8)模模糊糊有些熟悉。事实上(8)是经典的,它是拉普拉斯的一个公式,最早由雅可比证明。(9)出现在罗杰斯1907的一篇论文里。作为一位定积分专家,我也许可以证明(5)和(6),后来的确做到了这一点,尽管遇到的麻烦比我预想的要多得多。总之,积分公式看来没给人留下什么特别印象。
我发现级数公式(1)一(4)更有趣,很快就明显看出,拉马努金一定掌握了更基本的原理,袖里还有乾坤。第二个是勒让德(A.M.Legendre)级数理论中很著名的一个鲍尔(Bauer)公式,但其余的公式看似简单实际很难。如今可以在贝利(Bailey)关于超几何函数的剑桥小册子中找到这些公式的证明。
公式(10)一(13)有着截然不同的水准,显然既困难又深奥。椭圆函数方面的专家能够立刻看出(13)是以某种方法从“复乘法”理论中推导出来的,但(10)一(12)完全难倒了我,我从未见过与它们有丝毫相像的公式。单单瞧一眼就足以明白这些公式只能出自最高级的数学家之手。它们一定是对的,否则的话,没人能具有这样的想象力去发明它们。最后(你必须记住当时我对拉马努金一无所知,不得不考虑每种可能性),作者必定完全诚实,因为具有这种不可思议的水平的小偷和骗子比伟大的数学家更难找到。
最后的两个公式分开列出是因为它们不正确,这表现了拉马努金的局限,但仍然足以作为拉马努金非凡才能的额外证据。(14)中的函数是系数的真正近似,尽管不像拉马努金想象的那么接近。可以说,拉马努金的错误式子是他曾做出的最富成果的工作之一,因为它最终指引了我们在划分数上的一切合作研究。最后(15),虽然确实是“对的”,却一定会使人误解(拉马努金真的陷入了误解)。作为一个近似,式中的积分并不比1908年兰道(Landau)发现的简单函数
(16)
更精确。拉马努金因素数分布问题的一个错误类推被引入歧途。我稍后再谈拉马努金在数论方面的工作。
若要细究,必定会看出,拉马努金很大一部分的工作是早已发现的。他面临着不可逾越的障碍,一个贫穷孤寂的印度人和欧洲人世代积累起来的智慧拼脑子。他根本未曾得到真正的教育,印度没人有这个水准教他。他充其量只能见到三四本高质量的书,都是英语的。有段时间,他去了马德拉斯的图书馆,但那不是一个好的图书馆,只有极少的几本法文或德文书,而且无论如何拉马努金对这两门语言一窍不通。我估计拉马努金在印度的最好工作大约三分之二是再发现,在他有生之年,只有相当少的一部分发表出来,不过沃森系统研究他的笔记本后发掘了更多的东西。
拉马努金发表的大部分工作是在英国做出的,他的头脑已经僵化到一定程度,根本不可能变成“正统”的数学家,但他还是学会了做新的工作,而且做得非常棒。系统地从头教他是不可能的,但他逐渐吸收了一些新观念。特别是他学会了什么叫证明,他后期的论文,虽然在某些方面和从前一样奇异和特别,但读来已像受过良好教养的数学家的作品。不过他的方法和工具实质上从未变更。有人可能以为拉马努金这样的形式主义者会对柯西(Cauchy)定理着迷,可是他从未用过它,他形式方面才能的最惊人的明证就是他从没有必要用它。
很容易将拉马努金再发现的定理汇编成一个令人印象深刻的表。这样一个表当然不会很清晰,因为有时他只发现了定理的一部分,有时虽然发现了完整的定理,但只要他能彻底理解这个定理,就能找到证明,而他却没找到。例如,在解析数论中,从某种意义上说他发现了很多,但远未理解这门学科的真正难点。他的一些工作,主要是椭圆函数论方面,仍然有好些没弄清楚的地方。在沃森和莫德尔尽力研究之后,还是不可能区分哪些是他蒙出来的,哪些是他自己真正发现的。我只选取其证明在我看来还算清楚的例子。①也许从未用过。在《论文集》第129页有一处“余数理论”的引用,但我确信这是我本人写的。一一原注
在这里我得承认我该受责备,因为有许多事情我们现在想知道,而我原可以轻易弄清楚。我几乎天天见拉马努金,稍加探问就能澄清大部分疑问。拉马努金能够而且愿意坦率回答,丝毫不会对他的成就故弄玄虚。我几乎没有问过他哪怕一个这种问题,我甚至从未问过他是否(我想他一定读了)读过凯莱(Cayley)的或格林希尔(Greenhill)的《椭圆函数》。
现在我对此表示抱歉,但此事并不真的有关紧要,其实是很自然而然的事。首先,我不知道拉马努金会死。他也不爱整天惦记着自己的过去和心理活动,他是一个热心工作的数学家。归根结底,我也是数学家,一个数学家遇到拉马努金之后有的是远比回顾过往更有意思的事情值得去想。当拉马努金几乎每天都将半打新公式拿给我看时,为他如何发现这个或那个已知的定理而去烦他好像很可笑。
【资料】印度数学家拉马努金(二)
【资料】印度数学家拉马努金(一)
我认为拉马努金在古典数论中发现的不多,或者说他了解的确实也不多。任何时候他对算术形式的一般理论都一无所知,我怀疑在来这里之前他是否懂得二次互反律。丢番图方程应该很适合他,但他在这方面做得比较少,做出的也不是他最好的工作。他给出欧拉方程
(17)
的解形如
(18)
以及
(19)
但这两个都不是一般解
他重新发现了施陶特(von Staudt)关于伯努利数的著名定理:
(20)
其中是使得是约数的奇素数,是一个整数。很难说出他在何种意义上证明了这个定理,因为发现它时,他还几乎不明确知道什么是证明。正如利特尔伍德所说:“证明一词的清晰定义,如今人们已经太熟悉了,几乎相信这是与生俱来的概念,可他也许根本还不懂它。有时偶尔会出现一点有意义的推理片断,论据和直觉的彻底混合让他确信,除此之外他就不管了。”稍后我将谈一谈这个关于证明的问题,但要推迟到更重要的一段中。在这个定理上,还没有什么明显超出拉马努金的证明能力范围的东西。
很重要的一部分是关于数论的,特别是将整数表示成平方数之和的理论,它与椭圆函数理论关系密切。例如能表示成两个平方数的之和的的表示方法个数是
(21)
其中 是形如的的因数的个数,是形如的的因数的个数,雅可比给出了4,6,和8个平方数的类似公式。拉马努金发现了所有这些,还有相同类型的另外一些公式。
他还发现了勒让德定理,即可写成3个平方数之和,除非它具有
(22)
的形式。但我不认为他发现这个算是多重要的事情。这个定理极易猜到但难以证明。所有已知的证明都依赖于三元形式的一般理论,而拉马努金对此一无所知,我同意迪克森(Dickson)教授认为他很可能一点儿也没掌握这一理论的观点。无论如何他对于表示的数目一无所知。
这样,拉马努金在来英国之前,对数论的贡献寥寥无几。但若不能理解他对数字本身的热爱,便无法理解他。我曾写道:
他能以几近不可思议的方式记住数字的特性。利特尔伍德先生评价(我相信是他说的)“每个正整数都是他的私人朋友。”我记得有一次,他在帕特尼卧病在床,我去探望他。来时坐的出租车号是1729,我说,这个数字(=7×13×19)在我看来相当无趣,但愿这不是什么不祥之兆。“不”他回答道“这是个非常有趣的数,它是最小的能以两种不同方式写成两立方和的数。①”我自然而然地问他,能否告诉我四次方情况下的解是多少,想了一会儿之后,他回答说,找不到明显的例子,他认为这样的第一个数一定非常大。②
①——原注
②已知的最小数例由欧拉给出:——原注
在代数方面,拉马努金的主要工作涉及超几何级数和连分数(当然我是在传统意义上用代数这个词的)。这些课题简直是为他量身定做的,他是这些领域中无可非议的大师之一。现在有三个著名的恒等式,“杜格尔(Dougall)—拉马努金恒等式”:
(23)
其中
和“罗杰斯-拉马努金恒等式”:
(24)
英国数学家比拉马努金更早发现这些恒等式,我将在其他的演讲中谈论这些恒等式。至于超几何级数,可以粗略的这么说,他重新发现了规范理论,这理论发表贝利的小册子里,直到1920年才为人们所知。卡尔的书中谈到过一些这个理论,克里斯托尔(Chrystal)的《代数学》中写得更多,无疑拉马努金是从这些书起步的。(1)一(4)这四个公式是他超几何级数工作中非常独特的例子。
他在连分数方面的杰作是包含定理(10)一(12)的关于
(25)
的工作。这一分数理论依赖于罗杰斯—拉马努金恒等式,罗杰斯在拉马努金之前做出了这个工作,但他在别的方面超过了罗杰斯,而且我所引用的定理是拉马努金自己发现的。他还得出其他的许多适用范围广而且相当漂亮的公式,其中像拉盖尔(Laguerre)公式的
(26)
是极独特的例子。沃森①最近证明了其中最令人印象深刻的公式。拉马努金的工作也许在这些领域中做得最好。我曾写下:
①见G,N.沃森,“剑桥哲学会进展。,1935,卷31,第7页。
他对代数公式的洞察力,无穷级数变换的能力等等,实在是最令人惊羡的。在这方面,我绝未见过堪与他旗鼓相当的人,只能拿他和欧拉或雅可比相提并论。他远比大多数现代数学家更偏好从归纳数例中得出结果,比方说,他对划分数的同余性质研究,就完全是这么来的。然而凭着他的记忆力,耐心,计算能力,再综合起他归纳推广的力量,对数学形式的直觉,迅速修正自己假设的能力——这些往往着实令人称奇——使得他,在他自己的领域内,当世无人可敌。
如今,我绝不认为这种特别激烈的措辞太言过其实。也许公式的伟大时代已然结束,拉马努金原该生在100年前;但他至今仍是他的时代中最伟大的公式主义者。过去50年里,有的是比拉马努金更重要的——我猜有人一定会说是更伟大的——数学家,然而无人能在他独有的领域中对抗他。若要玩一场他懂得比赛规则的游戏,他可以让给世界上任何数学家15分。
在分析方面,拉马努金的工作定然不会给人以深刻印象,因为他不懂函数论,离开函数论就无法从事真正的分析。他从卡尔或其他的书中只能学到积分的形式部分,而这些已经被人反复和深入细致地研究过了。然而拉马努金仍然重新发现了数量惊人的最为优美的解析恒等式。黎曼Zeta函数的函数方程
即
(27)
(用一种几乎认不出来的符号)记在笔记本中。还有泊松(Poisson)的求和公式
(28)
其中
且。此外还有阿贝尔函数方程
(29)
其中
最近沃森,蒂奇马什(Titchmarsh)和我自己做的关于“傅里叶(Fourier)函数核”及“反商函数”的工作,大部分的基础规范思想都来源于拉马努金,当然他能够求出任何可求值的定积分的值。有一个特别有趣的公式,即
(30)
这个公式他特别喜欢,老是用它。这是一个真正的“内插公式”,它使我们可以得出一些结论,例如在一定条件下,自变量的所有正项积分值为零的函数一定也为零。虽然这个公式与梅林(Mellin)及其他人的工作密切相关,但我从未见到过其他人明确地论述过它。①这个方程被罗杰斯重新发现,而且罗杰斯在《论文集(337页)》中认为是他的发现;但在阿贝尔死后未完成的作品中也发现了这个方程。——原注
还剩下拉马努金早期工作中最迷人的最后两个方面,椭圆函数和解析数论。第一方面,除了专家以外,可能任何人都会认为它太过专业复杂,难于理解,现在我不打算谈它,第二个科目其实更难(读过兰道关于素数的书或英哈姆[Ingham]小册子的人都知道这一点),但人人都能大致理解这个课题中的问题,而且每个不错的数学家都能大概明白何以这些问题击败了拉马努金。这是拉马努金真正的失败,一如既往,他展示了惊人的想象力,但随后他什么也没证明,甚至他想象的也有许多是错的。
这里我不得不就一个非常困难的题目多说几句:证明及其在数学中的重要性。一切物理学家和许多非常可敬的数学家都轻视证明。例如,我听说埃丁顿教授认为:“纯粹数学家理解的那种证明,实在乏味之极而又无足轻重,确定自己发现了某种好东西后,谁会再浪费时间去寻找证明呢?”事实上埃丁顿是自相矛盾的,有时他甚至屈尊去做证明。对于他来说,只知道宇宙中正好有个质子并不够,他禁不住诱惑要去证明它。我不禁想,无论这个证明的价值怎样,它给他带来了某种智力上的满足感。毫无疑问他会辩解说“证明”对他和对一位纯粹数学家的意义截然不同,无论如何我们不必过多地去咬文嚼字。但对于他的观点——我相信这观点也是几乎所有物理学家都打心底同意的——身为数学家,我有义务做出某种答复。
我不打算纠缠于分析一个特别微妙的概念,但我想,关于证明,有几个观点是差不多所有数学家都赞成的。首先,即使我们并不确切地理解什么是证明,但不管怎样,在普通分析中,我们看到证明时,总能认出来。其次,在任何证明的叙述中都有两个不同的动机,第一个动机是保证结论的说服力,第二个动机是,从一系列已知正确的命题开始,把它们按一定顺序排列起来,按惯用的模式推论,最后得出所要的结论。经验表明,除了在最简单的数学中,这两种动机,如果不实现第二个,就几乎不可能实现第一个。我们可以直接看出5或17是素数,但如果不去证明,没人能确信是一个素数。没人能拥有这样生动和深刻的想象力。
数学家经常通过直觉的尝试来寻找定理,结论看来似乎是对的,于是他着手于构造证明。有时候这是按部就班的流程,任何受过良好训练的专业人员都能完成,然而想象往往是极不可靠的向导。在解析数论中尤其如此,连拉马努金的想象力也将他引入不可救药的迷途。
有一个惊人的错误假设,我经常用它作为范例,它甚至差点得到高斯的认可,驳倒它花了大约100年的时间。解析数论的中心问题是素数分布问题。小于一个大数的素数个数大约为
(31) ;
这就是“素数定理”,数学家们早就猜到了它,但直到1896年被阿达玛(Hadamard)和瓦莱—普桑证明后,这个定理才算是站住脚了。去掉近似误差,更好的结果是
(32)①
在某些情况下,更精确的结果是
(33)
(现在我们不必为级数构成的规律而烦恼)。很自然地推出,对无论多么大的
(34)
①取积分主值
高斯和其他数学家都认为这个猜想非常可能是真的。这个猜想不但看起来有道理,而且得到所有事实的佐证。已知有10000000个素数,其数字间隔甚至达到1000000000,对于其中每一个值(34)都是正确的。1912年,利特尔伍德证明了这个假设是错误的,存在无穷多个的值使得(34)中的不等号必须反过来。特别地,存在一个数使得对于小于的某个,(34)是错的。利特尔伍德证明了的存在性,但他的方法并不能给出一个值,直到最近,斯凯维斯(Skewes)①才发现了一个可采用的值,即,我认为这是数学中适用于某个明确目的的最大的数。宇宙中质子的个数大约是。国际象棋的可能局数更大一些,也许是·。(无论如何它一定是一个二重阶指数)。如果宇宙是棋盘,质子是棋子,任意位置的两个质子的交换是一着,那么可能的棋局数就类似于斯凯维斯数。无论通过改良斯凯维斯的讨论可以将该数减小多少,看来我们是不可能知道关于利特尔伍德定理正确性的例子了。
这个例子中,真理不仅击败了所有事实证据和常识,而且甚至击败了属于高斯的那样有力而深刻的数学想象力,当然它是从数论最困难的部分中选出来的。素数理论中没有真正容易的部分,不过也可以谈谈某种简单的讨论,虽然这种简单讨论不能证明什么,却也确实不会误导我们。
①S。斯凯维斯,伦敦数学会杂志,1933,卷8,277页。——原注
例如,简单的讨论可能会引导好的数学家得到素数定理的结论
(35)①
或者,可得到等价结论
(36)
其中是第个素数。
首先,我们可以从欧拉恒等式开始
(37)
这个式子对s>1是正确的,但对于s=1,级数和乘积变成无穷。讨论自然可以推出,当s=1时,级数和乘积应以相同方式发散,同理
(38)
后一项级数在s=1时为有限值,自然地推出
像那样发散,
或者更精确地,对于大数
(39)
①意思是比趋于1。
又因为
所以公式(39)蕴涵了近似等于。
有一个似繁实简的论证。
容易看出,能除尽的素数的最高次幂是
其中表示的整数部分。因此
(40)
由斯特灵(Stirling)定理知,(40)的左端实际上是。至于右端,人们可以认为,素数的平方,立方,..…·相对而言比较罕见,包含它们的项应当是不重要的,如果我们用代替 ,引发误差可以忽略不计。因而我们推出
这恰恰再次符合了约等于的结论。
这就是切比雪夫(Tchebychef)详细推理过程的大略。他是第一个在素数理论中取得实质性进展的人,我想象拉马努金也是以同样的方式开始的,尽管笔记本上没有什么能表明这一点。唯一可以肯定的是,拉马努金独立发现了素数定理的形式,这是一项重大成就,在他之前发现这个定理的形式的人,如勒让德、高斯和狄利克雷(Dirichlet),都是非常伟大的数学家。拉马努金还发现了其他一些更为深刻的公式,也许最好的例子是(15),用简单函数(16)代替积分会更精确些,但正如它所表示的和1909年兰道证明的那样,拉马努金的公式是正确的,而没有什么明显的事实能引导他推出这一真理。
剩下要说的事实是,拉马努金在这一领域的工作几乎没有什么持久的价值。解析数论是数学中一个特殊的分支,其中证明实际上就是一切,而缺乏绝对的严格则一文不值。发现素数定理的数学家的成就与那些发现其证明的人相比是不足挂齿的。不仅在这一理论中(如利特尔伍德定理表明的)没有证明就不能确信任何事实,虽然这事实本身可能很重要。素数定理以及其他这一学科中重要定理的整个历史表明,除非掌握了证明,否则不可能真正理解这一理论的结构和意义,也没有什么可靠的直觉能引导你进行下一步的研究。做出聪明的猜想是比较容易的,有些定理,像“哥德巴赫定理”①至今没有任何人能证明它,但连傻瓜也可能猜想到它。
①任何大于2的偶数都是两个素数之和。——原注
素数理论依赖于黎曼函数的性质,尤其是其零点的分布,是复变量s的解析函数。而拉马努金对解析函数理论一无所知,我曾写道:
对复变函数理论的无知毁了拉马努金的素数理论。这是(这么说吧)如果黎曼函数没有复零点,他这个理论就是正确的。他的证明方法依赖于大规模使用发散级数,……可以猜到,他的证明肯定是站不住脚的。而更离谱的是,许多事实结果也弄错了。尽管用了不正确的方式,他的确得到了经典公式的主项;不过其中没有一个能给出他指望的精确近似度。
可以说这是拉马努金的一场惨痛失败。……
如果我当初就此打往,那我也不必再多说什么。但我再一次放任自己感情用事。我继续议论“他的失败比他的一切成功更美丽”,那自然是荒谬的言过其实。试图把失败伪装成别的什么是无济于事的。也许我们可以这样说,他的失败,从另一个角度看,应当增添而不致减少我们对他天赋的敬慕,因为它给了我们额外的和惊人的佐证,证明他的想象力和全能性。
然而,数学家的声誉不能建立在失败的尝试和重新发现上,而根本上、必须公正的扎根在确切的和创造性的成就之上。我必须立足于此,为拉马努金辩护,希望在此后的演讲中能做到这一点。
注释:这是1936年发表在哈佛文学和科学三百年纪念大会上的两篇演讲中的前一篇,并且形成了哈代的著作《拉马努金:关于他生平和工作的十二篇演讲》(剑桥,1940)的演讲l。第二篇演讲逐渐扩充成其余的十一篇演讲。无疑哈佛演讲稿出自哈代5月5日和同年5月20日在英国剑桥以“S,拉马努金的生平和科学工作”为题做的两次公开演讲,次年(1937,春季学期)他以“联系拉马努金工作的数学问题”为题开了24节课程。