统计学知识梳理（一）二项分布、泊松分布、大数定律

一、统计学基础知识

1、总体（population）和样本（sample）：

• 总体：研究对象的整个群体。
• 样本：从总体中选取的一部分。

2、总体和样本的方差：

总体方差:

样本方差：

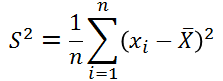
取样时，有可能样本均值很接近总体期望，这时候这个公式和实际就切合的比较好；但当样本均值与总体期望相差较大，往往会造成偏差。引出样本方差的无偏估计：

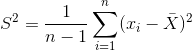
关于为什么分母是n-1的问题，参考这篇：彻底理解样本方差为何除以n-1，这里也引用一个更易于理解的解释：

首先要说的一点是，计算方差除的数并不是样本个数，而是自由度，至于自由度，可以理解为能够随机变化的变量的个数

举例子来说，对于任意a,b两个数，他的自由度是2，因为a,b不相关，可以随意变动

同样是a,b两个数，如果加上限定条件，a+b=6，还是两个变量，但是实际自由度只有1，因为a确定后，b的值是唯一的，实际有效的变量只有1个

切回统计来说，对于总体来说，每个变量之间是不相关的，自由度=变量个数，如果从总体中抽样，抽取的样本其实是符合总体的规律的，这就是在样本上加了个限定条件，就好比前面的a+b=6的条件一样，那么自由度就是抽取样本数-1

不知道这样没事是不是对的，至少可以便于理解了吧

3、标准差：
标准差是方差的算术平方根

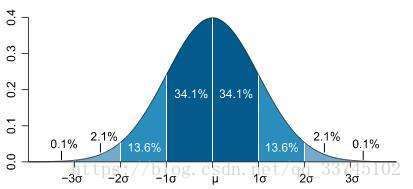
4、中心极限定理（central limit theorem）：
中心极限定理：样本平均值约等于总体平均值，且不管总体是什么分布，任意一个总体的样本平均值都会围绕在总体的平均值周围，并且呈正态分布。如下：

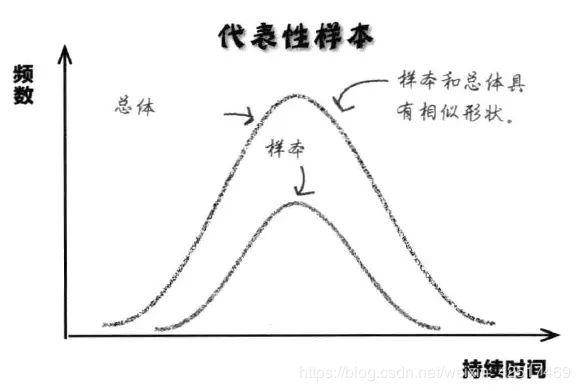
5、随机变量（Random Variable）：
随机变量其实是一个函数，将随机过程映射成实际数字，分为离散型随机变量和连续随机变量两种。

二、二项分布（Binomial Distribution）

1、二项分布是什么？

对于这个问题，我想转化成——什么样的分布才是二项分布？

满足以下三个条件的分布，就是二项分布：

（1）做某件事情的次数（也叫试验次数）是固定的，用n表示。例如，抛硬币3次，求婚101次等。

（2）每一次事件都有两个可能的结果（成功，或者失败）。例如每次求婚都有两种可能结果，被接受（成功），被拒绝（失败）。

（3）每一次成功的概率都是相等的，成功的概率用p表示。

看一个示例：某人篮球投篮的命中率是0.3，总共投篮10次，问至少投中2次的概率?

分析：

（1）每次投篮有2种结果，投中或没投中；

（2）每次投篮的投中概率是相同的，都为0.3；

（3）每次投篮可认为是独立事件。

因此，符合二项分布。

你感兴趣的是成功x次的概率是多少，那么就可以用二项分布的公式快速计算出来了。

2、二项分布的公式

知道了二项分布是什么，那么如何计算符合二项分布事件的概率呢？

很简单，用如下公式就可以计算出来。

其中，p表示成功的概率，x表示成功的次数。

3、 二项分布的期望：

期望就是我们所期望的最可能出现的值。n表示试验的总数，p表示每个试验中得到成功结果的概率，那么X的期望值如下:
　　　
如X表示投篮10次后进球的次数，每次命中率40%，E(X)=10*40%=4，表示投中四次的可能性最大。

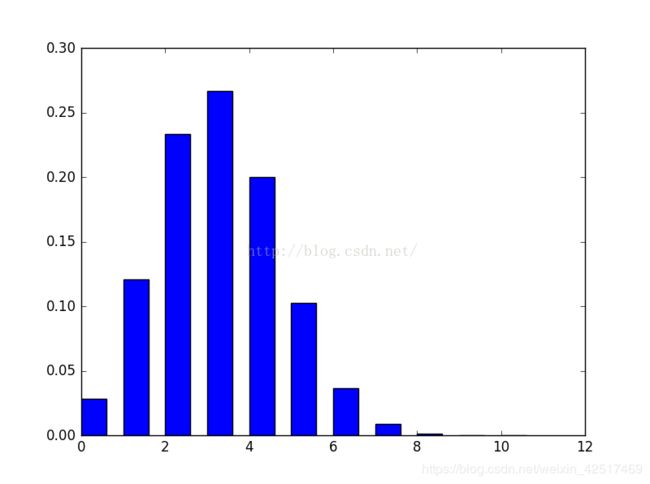
三、泊松分布（Poisson Distribution）

泊松分布描述的是一个离散随机事件在单位时间内发生的次数, 其对应的场景是我们统计已知单位事件内发生某事件的平均次数 λ, 那么我们在一个单位事件内发生 k次的概率是多大呢? 比如说假设某个路口一小时内通过的车辆数是3辆，那么在接下来的一个小时内, 通过 0 辆车， 1辆车，10 辆车, n 辆车的概率分别是多少呢? 泊松分布给出了定量的结果 :
$$p(X=k)=\frac{e^{-\lambda }{\lambda }^k}{k!}$$
其中 P(X=k) 描述的就是在单位时间内事件 X发生 k 次的概率, λ 代表在单位时间内事件发生的平均次数, 也就是泊松分布的 期望, 同时也是方差。

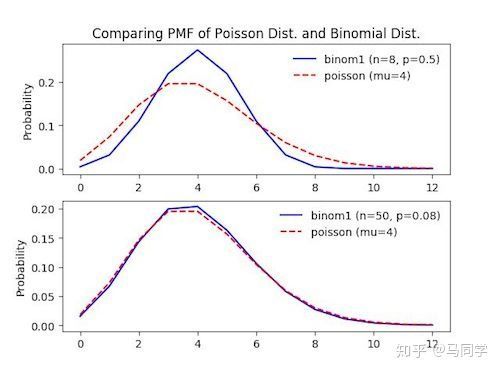
也可以理解成泊松分布是二项分布的一种特殊形式：当二项分布的 p 很小, n很大的时候, 二项分布可以用泊松分布近似.

泊松分布公式推导：

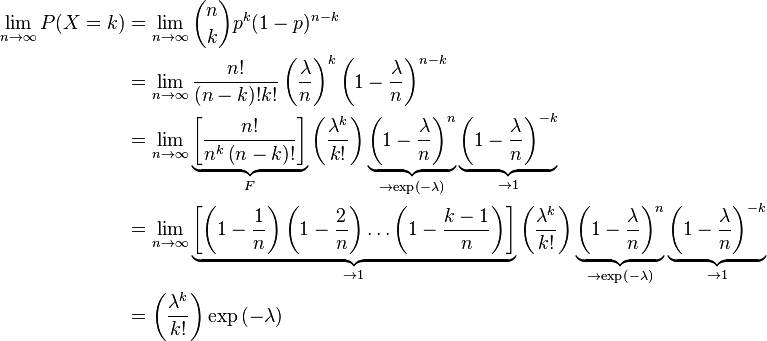
附上马同学通俗易懂的文章：如何通俗理解泊松分布

四、大数定律(Law of Large Numbers)

1、赌徒谬误（The Gambler’s Fallacy）

赌徒谬误的来源是因为将前后互相独立的随机事件当成有关联而产生的。怎么样算是独立的随机事件呢？比如说，抛硬币一次，是一个随机事件。再抛一次，是另一个随机事件。两个事件独立的意思是说，第二次的结果并不依赖于第一次的，互相没有关联。假设硬币是理想对称的，将出现“正”记为1，“反”记为0，那么，每次结果为1和0的概率都是1/2。第二次“抛”和第一次“抛”互相独立，再多“抛”几次也一样，每次的“抛丢”事件互相独立，出现1和0的概率总是“1/2，1/2”，都和第一次一样。即使硬币不对称，比如两面之概率可能是“2/3，1/3”，也并不会影响每次投丢的“独立性”，每次得到正面的概率都是2/3，并不受上一次结果的影响。

2、大数定律

大数定律是描述相当多次数重复实验的结果的定律。根据这个定律知道，样本数量越多，则其平均就越趋近期望值。

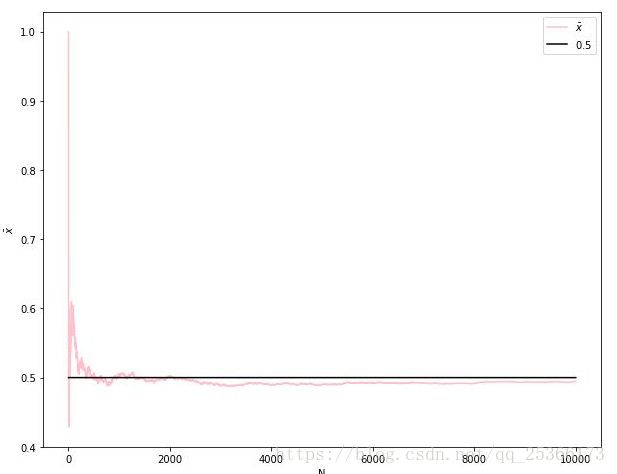
或者说，当n趋于无穷时，样本均值趋于总体期望值。

五、正态分布(normal distribution)

正态分布也叫高斯分布或钟形曲线。则其概率密度函数为：

正态分布的数学期望值或期望值$\mu$等于位置参数，决定了分布的位置；其方差${\sigma }^2$的开平方或标准差$\sigma$等于尺度参数，决定了分布的幅度。

正态分布的概率密度函数曲线呈钟形，因此人们又经常称之为钟形曲线（类似于寺庙里的大钟，因此得名）。

正态分布在生活中非常常见，这里参考马同学的文章：为什么正态分布如此常见？