自然语言处理入门练习（一）：基于机器学习的文本分类及实战（附代码）

自然语言处理入门练习（一）：基于机器学习的文本分类及实站（附代码）

任务一：基于机器学习的文本分类

1 文本分类任务简介

  在有监督学习中,需要提供一组有类别标记的样本用来学习模型以及检验模型的好坏。这组样本集合就称为数据集。数据集用X表示, X=(x1,y1),…,(xN,yN),N 为 样本个数。yi为样本实例xi的类别标记。在自然语言处理中,数据集也经常称为语料库。
  其中xi为一组文本，yi可以是一组标签如词性，也可以是一个标签如文本的类别。

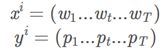
使用机器学习方法，即找到这样一个映射f，使得xi->yi。

2 向量化

  在机器学习算法中,样本实例一般是以连续变量或离散变量的形式存在的(也称为特征),而在自然语言处理中一般都是文字形式。因此,在进行学习模型之前,需要进行特征提取,将样本的原始表示转换为特征向量。
  在机器学习中,为了更好地表示样本的属性,一般将样本表示成代数形式,称为样本的特征,我们用ϕ(x)。样本特征可以是一维或多维向量,ϕ(x) ∈ Rm,m是向量维数。

  自然语言处理中,数据都是以字符形式存在的。样本的原始表示一般是字符串序列。为了便于使用机器学习方法,首先要把样本表示为向量形式。下面我们介绍几种常用的特征表示方法。自然语言处理的,在构造样本和样本集合之后,为了和后面的机器学习算法相结合,我们将样本x 转变成向量φ(x)。在将字符表示转换成向量表示的过程中需要很多中间步骤,我们把这些中间步骤都称为数据处理,并且尽可能的模块化。

2.1 词袋模型

  一种简单的方法是简单假设文本(如一个句子或一个文档)是由字、词组成的无序多重集合,不考虑语法甚至词序。这就是在自然语言处理和信息检索中常用的词袋模型，词袋模型可以看成一种以词为基本单位的向量空间模型(Vector Space Model, VSM)。

2.2 N元特征

  词袋模型在需要深层分析的场合就会显得太过简化了。例如在语义分析里,“你打了我”和“我打了你”,意思是相反的,但用词袋模型表示后,这两句话是向量表示的等价的,这显然是不合理的。
  N元特征(N-gram 特征),顾名思义,就是由 N 个字或词组成的字符串,单元可以是字或词。这里N是大于等于1的任意整数。如果N 为2,就叫做二元特征,如果N为 3,就叫做三元特征以此类推。
  N元特征可以看出是对词袋模型的一种改进方法。与 N元特征相关的概念是 N元语法模型。以中文句子“机器学习算法”为例,以字为基本单位的二元特征集合为:{机器,器 学,学习,习算,算法}。集合中每一项都是由二个相邻的字组成的的子串,长度为 2。这些子串可以是有意义的词(例如:“学习”、“算法”),也可以是无任何意义的字符串(例 如:“器学”,“习算”)。但是这些无意义的子串也有可能在分类中起到很关键的作用。一个长度为L的句子,可以提取出L − 1个二元特征。
  有了N元特征集合,就可以利用词袋模型将文本表示为向量形式。随着 N的增加, 可以抽取的特征就会越多,特征空间也会呈指数增加。这些高阶的特征出现的频率也会相对较低,对分类不但没有太多帮助,还会直接影响着后续处理的效率与复杂度。因此在一般的文本分类任务中,N 取 3 就足够了,并且同时也使用一元和二元特征,防止出现过拟合。

3 文本分类

  经过特征抽取后,一个样本可以表示为 k 维特征空间中的一个点。为了对这个特征空间中的点进行区分,就需要寻找一些超平面来将这个特征空间分为一些互不重叠的子区域,使得不同类别的点分布在不同的子区域中,这些超平面就成为判别界面。
  为了定义这些用来进行空间分割的超平面,就需要引入判别函数的概念。假设变量 z ∈ Rm为特征空间中的点,这个超平面由所有满足函数f(z) = 0的点组成。这里的f(z) 就称为判别函数。
  有了判别函数,分类就变得很简单,就是看一个样本在特征空间中位于哪个区域, 从而确定这个样本的类别。 判别函数的形式多种多样,在自然语言处理中,最为常用的判别函数为线性函数。

3.1 二分类问题

  sign为符号函数，取判别函数f(z)的正负号，为方便，简写判别函数为

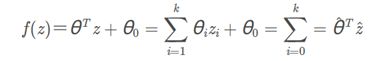
其中z0=1, θˆ，zˆ分别称为增广权重向量和增广特征向量。

  后面的分类器描述中,我们都采用简化的表示方法,并直接用 θ，z来表示增广权重向量和增广特征向量。

3.2 多分类问题

  对于 C类分类问题,需要定义 C个判别函数。但是这种表示一般适用于类别 y 为离散变量的情况。在自然语言处理的很多学习任务,类别 y 可以是更复杂的结构,比如多标签、层次化以及结构化等形式。为了更好的描述这些情况，可采用如下形式：

  这里ϕ(x,y)是包含了样本x和类别y混合信息的特征向量，θ=[θ1;θ2…;θC]
例子：

其中x=w1…w∣V∣，是个字典大小的向量。
  总之：

其中：

ck是字典中第k个词。

labelm表示第m个标签。
  再论式3.2：
  ϕ(x,y)为特征表示，f(ϕ,θ)为模型，一般在文本分类中为线性模型（由于我们可以构建足够复杂的特征表示，在高维空间中总是线性可分的），argmax 为解码过程，即寻求y解的过程，对于分类问题，看得分取高分即可。机器学习要学的参数是θ。

4 词性标注

  y的输出值可能不仅仅是分类值，可能也是一个序列值，如词性标注问题,输入一个序列，输出也是一个序列：

X：(S) I give you a book (E)
y: P V P D N

其中P为代词，V为动词，D为冠词，N为名词，(S)为开始符，(E)为结束符

1. 初级处理方法：
   如(I, P),(give, V),(you,P),(a,D),(book,N) 构建一个多分类器。
2. 进阶处理方法：
   由于一个词的词性与其上下文相关，可以构建大小为n窗口，如n为1。
   可以增加以下：
   ((S) I give, N), (give you a, P)…
   通过构建一个特征更多的多分类器。
   但是仍然存在一个问题：相近词的词性约束缺失。
3. CRF(条件随机场)：
   
   L为序列化输出y的长度。
   其中ϕ(x⃗ ，y)中特征抽取方式如下，假定窗口为1：
   
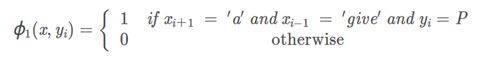
   其中ϕ∗(x⃗ ,yi−1,yi)中特征抽取方式如下:
   

5 感知器训练

5.1训练算法

输入:训练集: (xi,yi)，i=1,⋅⋅⋅,N
最大迭代次数:T
输出: θk

θ0=0;
k=1；
for t=1⋅⋅⋅T do

shuffle

for i=1⋅⋅⋅N do 

选取一个样本 (xi , yi );
预测类别 yˆt

if yˆt=yt then
θk=θk−1+(φ(xt,yt)−φ(xt,yˆt));
k=k+1;
end
end
end
return θT;

算法要点：

1. 单个样本进行学习
2. 被动学习，只有预测值和实际值不同时才更新
3. 每次一轮迭代前进行shuffle
4. early-stop避免过拟合，将集合分成训练集、开发集和测试集。

5.2 感知器收敛性

5.2.1 定义

  多类线性可分: 对于训练集D=(xi,yi)i=1ˆn,如果存在一个正的常数γ(γ > 0)和权重向量θˆ∗,并且∥θˆ∗∥=1,对所有i都满足 ⟨θˆ∗,φ(xi,yi)⟩−⟨θˆ∗,φ(xi,y)⟩>γ,y̸=yi(φ(xi,yi )∈Rˆm为样本xi的增广特征向量),那么训练集D 是线性可分的。

5.2.2 定理

  对于任何线性可分的训练集D=(xi,yi)i=1n,假设 R 是所有样本中错误类别和真实类别在特征空间 φ(x, y) 最远的距离。

  那么在5.1感知器学习算法中,总共的预测错误次数K<γˆ2/Rˆ2

【核心代码】

lr_model.py

import tensorflow as tf


class LrModel(object):
    def __init__(self, config, seq_length):
        self.config = config
        self.seq_length = seq_length
        self.lr()

    def lr(self):
        self.x = tf.placeholder(tf.float32, [None, self.seq_length])
        w = tf.Variable(tf.zeros([self.seq_length, self.config.num_classes]))
        b = tf.Variable(tf.zeros([self.config.num_classes]))

        y = tf.nn.softmax(tf.matmul(self.x, w) + b)

        self.y_pred_cls = tf.argmax(y, 1)

        self.y_ = tf.placeholder(tf.float32, [None, self.config.num_classes])
        cross_entropy = tf.reduce_mean(-tf.reduce_sum(self.y_ * tf.log(y), reduction_indices=[1]))
        self.loss = tf.reduce_mean(cross_entropy)

        self.train_step = tf.train.GradientDescentOptimizer(0.5).minimize(cross_entropy)

        correct_prediction = tf.equal(tf.argmax(y, 1), tf.argmax(self.y_, 1))
        self.accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))

【完整代码github地址】

https://github.com/chenlian-zhou/nlp/tree/master/nlp_induction_training/task1

【参考资料】

1. https://github.com/FudanNLP/nlp-beginner
2. https://github.com/FudanNLP/nlp-beginner/blob/master/%E6%96%87%E6%9C%AC%E5%88%86%E7%B1%BB.md