van Emde Boas tree
原链接
介绍
van Emde Boas tree是一种适用于0-u数据存储的一种数据类型。它每次根据u的一半来依次递减,直到最后减少到2为止。对数据有一定要求:要求u是2的2k或者2k+1次方。
单个结点的结构如下: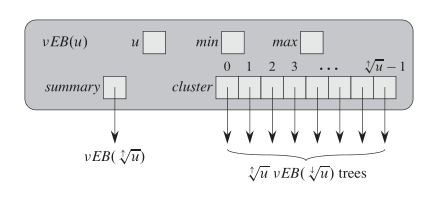
每个结点包含以下数据:其中u是当前结点的cluster的数量;min和当前结点中最小结点的数,而且最小值不出来在cluster当中; max是当前结点中最大结点的数;其中min和max在根结点和在子结点中的定义不一样,在根结点中,直接就是数据的值,而在子结点中,则是结点在当前结点中的cluster的序号;summary是一个指向子summary结点的指针,cluster是指向当前子cluster结点的指针。
下面看一个例子: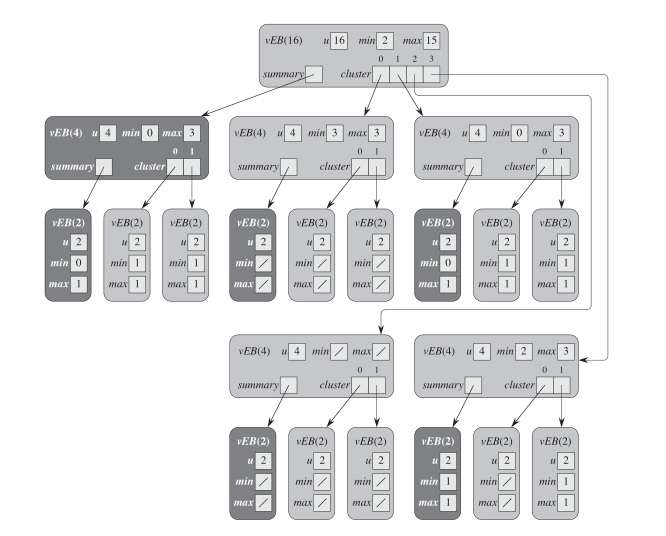
以上是一个数据集合{2,3,4,5,7,14,15}的van Emde Boas Tree图。可以看到,在最基结点,就是u==2的结点是,summary和cluster是没有的,只保存有min和max的值。
实现
下面来看下代码是如何实现它的,首先,根据上面结点的结构,我们来定义树的结构:
typedef struct Node_
{
int u;
int min;
int max;
struct Node_ *summary;
struct Node_ **cluster;
}Node;
typedef struct VanEmdeBoasTree_
{
Node *root;
}VanEmdeBoasTree;
static VanEmdeBoasTree * g_VEB = nullptr;
然后,再来初始化这颗树,我们要定义一个数据的开始长度,而所有的数据大小不能超过这个值。
void createCluster(Node *cluster, int u)
{
cluster->u = u;
cluster->min = NIL;
cluster->max = NIL;
if (2 == u)
{
cluster->cluster = nullptr;
cluster->summary = nullptr;
}else
{
int sqrt_u = (int)sqrt(u * 1.0);
cluster->summary = new struct Node_;
createCluster(cluster->summary, sqrt_u);
cluster->cluster = new struct Node_ *[sqrt_u];
for (int i = 0; i < sqrt_u; ++ i)
{
cluster->cluster[i] = new struct Node_;
createCluster(cluster->cluster[i], sqrt_u);
}
}
}
void init(int u)
{
g_VEB = new VanEmdeBoasTree;
g_VEB->root = new Node;
createCluster(g_VEB->root, u);
}
刚开始里面是没有任何数据的。接着我们先对其做一些简单的基本操作,比如求最小值和最大值:
int min(Node *node)
{
return node->min;
}
int max(Node *node)
{
return node->max;
}
这个最简单了,因为根结点里面就已经自带了。
接着在讲查询之前,我们先要进行定义几个公式:就是根据给定的一个数,求出它所在的cluster以及它所在的cluster内的序号。
int high(int x, int u)
{
return (int)floor(x / sqrt(u * 1.0));
}
int low(int x, int u)
{
return x % (int)sqrt(u * 1.0);
}
high函数可以求出给定的值所在的cluster,low可以求出给定的值所在的cluster内的序号。接着便是根据x的high值和low值可以求出x的值是多少:
int index(int x, int y, int u)
{
return x * (int)sqrt(u * 1.0) + y;
}
以上3个公式中u的值皆是当前结点的u值。
那么查询就简单了:
bool member(Node *node, int x)
{
if (node->min == x || node->max == x)
{
return true;
}else if (2 == node->u)
{
return false;
}else
return member(node->cluster[high(x, node->u)], low(x, node->u));
}
如果和最大或者最小相等那么肯定存在,而如果找到基结点去了,则不存在,如果不满足以上条件则继续往下查找。
接着便是前驱和后继:
int successor(Node *node, int x)
{
if (2 == node->u)
{
if (0 == x && 1 == node->max)
{
return 1;
}else
return NIL;
}else if (NIL != node->min && x < node->min)
{
return node->min;
}else
{
int max_low = max(node->cluster[high(x, node->u)]);
if (NIL != max_low && low(x, node->u) < max_low)
{
int offset = successor(node->cluster[high(x, node->u)], low(x, node->u));
return index(high(x, node->u), offset, node->u);
}else
{
int succ_cluster = successor(node->summary, high(x, node->u));
if (NIL == succ_cluster)
{
return NIL;
}else
{
int offset = min(node->cluster[succ_cluster]);
return index(succ_cluster, offset, node->u);
}
}
}
}
int predecessor(Node *node, int x)
{
if (2 == node->u)
{
if (1 == x && 0 == node->min)
{
return 0;
}else
return NIL;
}else if (NIL != node->max && x > node->max)
{
return node->max;
}else
{
int min_low = min(node->cluster[high(x, node->u)]);
if (NIL != min_low && low(x, node->u) > min_low)
{
int offset = predecessor(node->cluster[high(x, node->u)], low(x, node->u));
return index(high(x, node->u), offset, node->u);
}else
{
int pred_cluster = predecessor(node->summary, high(x, node->u));
if (NIL == pred_cluster)
{
if (NIL != node->min && x > node->min)
{
return node->min;
}else
return NIL;
}else
{
int offset = max(node->cluster[pred_cluster]);
return index(pred_cluster, offset, node->u);
}
}
}
}
都是先在当前cluster中查找,如果当前cluster中查找不到,则到它的前一个或者后一个有数据中的结点中去查找。这里,唯一需要注意的地方就是,前驱判断的时候,当前结点不存在,在它的前一个结点中如果也没有找到有结点的数据的话,要注意还要判断是否有最小结点,如果有的话,这个也需要判断一下。
void insert(Node *node, int x)
{
if (NIL == node->min)
{
emptyInsert(node, x);
}else
{
if (x < node->min)
{
int tmp = x;
x = node->min;
node->min = tmp;
}
if (node->u > 2)
{
if (NIL == min(node->cluster[high(x, node->u)]))
{
insert(node->summary, high(x, node->u));
emptyInsert(node->cluster[high(x, node->u)], low(x, node->u));
}else
{
insert(node->cluster[high(x, node->u)], low(x, node->u));
}
}
if (node->max < x)
{
node->max = x;
}
}
}
插入操作的话,如果当前结点没有结点的话,则直接赋值最小和最大结点值就好了。或者的话,则需要和最小值比较,并且根据插入的值查找适合的cluster插入并且根据修改summary记录当中cluster的值。插入完成以后在判断是否需要修改最大值。
删除操作的话相对复杂一些:
void vBEDelete(Node *node, int x)
{
if (node->min == node->max)
{
node->min = NIL;
node->max = NIL;
}else if (2 == node->u)
{
if (0 == x)
{
node->min = 1;
}else
{
node->min = 0;
}
node->max = node->min;
}else
{
if (x == node->min)
{
int first_cluster = min(node->summary);
x = index(first_cluster, min(node->cluster[first_cluster]), node->u);
node->min = x;
}
vBEDelete(node->cluster[high(x, node->u)], low(x, node->u));
if (NIL == min(node->cluster[high(x, node->u)]))
{
vBEDelete(node->summary, high(x, node->u));
if (x == node->max)
{
int summary_max = max(node->summary);
if (NIL == summary_max)
{
node->max = node->min;
}else
{
node->max = index(summary_max, max(node->cluster[summary_max]), node->u);
}
}
}else if (x == node->max)
{
node->max = index(high(x, node->u), max(node->cluster[high(x, node->u)]), node->u);
}
}
}
如果是一个结点,则直接删除,如果是基结点,则修改最小和最大值为另一个结点。否则的话,往下遍历x结点所在的位置,如果需要删除的是最小结点,则直接重新找过一个最小结点,然后在cluster当中删除它。然后,判断cluster是否为空,如果为空的话,我们修改修改记录在summary当中的cluster信息并且修改最大值。或者,设置重新设置最大值。
我们测试下:
#include#include using namespace std; int _tmain(int argc, _TCHAR* argv[]) { static const int default_u = 16; init(default_u); insert(g_VEB->root, 2); assert(true == member(g_VEB->root, 2)); insert(g_VEB->root, 3); assert(true == member(g_VEB->root, 3)); insert(g_VEB->root, 4); assert(true == member(g_VEB->root, 4)); insert(g_VEB->root, 5); assert(true == member(g_VEB->root, 5)); insert(g_VEB->root, 7); assert(true == member(g_VEB->root, 7)); insert(g_VEB->root, 14); assert(true == member(g_VEB->root, 14)); insert(g_VEB->root, 15); assert(true == member(g_VEB->root, 15)); assert(14 == predecessor(g_VEB->root, 15)); assert(15 == successor(g_VEB->root, 14)); vBEDelete(g_VEB->root, 2); assert(false == member(g_VEB->root, 2)); vBEDelete(g_VEB->root, 3); assert(false == member(g_VEB->root, 3)); vBEDelete(g_VEB->root, 4); assert(false == member(g_VEB->root, 4)); vBEDelete(g_VEB->root, 5); assert(false == member(g_VEB->root, 5)); vBEDelete(g_VEB->root, 7); assert(false == member(g_VEB->root, 7)); vBEDelete(g_VEB->root, 14); assert(false == member(g_VEB->root, 14)); vBEDelete(g_VEB->root, 15); assert(false == member(g_VEB->root, 15)); finit(); return 0; }