常用激活函数总结与发展历程

一、什么是激活函数

神经网络中的每个神经元节点接受上一层神经元的输出值作为本神经元的输入值，并将输入值加权求和后传递给下一层，在多层神经网络中，上层节点的输出和下层节点的输入之间具有一个函数关系，这个函数称为激活函数（又称激励函数）。

二、激活函数的作用——为什么要使用激活函数

没有激活函数，无论神经网络有多少层，输出都是输入的线性组合。

激活函数给神经元引入了非线性因素，使得神经网络可以逼近任何非线性函数，这样神经网络就可以应用到众多的非线性模型中。

 

正因为上面的原因，为神经网络引入非线性函数的激活函数，才可以充分发挥层叠加所带来的优势，以逼近任意函数。

三、常用的激活函数及发展历程

1.Sigmoid ——

最早的激活函数，图像如下图所示：

sigmoid的优点

1.输出值有限，在0-1之间,有限输出使得对一些比较大的输入也有较平稳的表现

2.函数光滑可微，导数计算方便

sigmoid的缺点

1.涉及指数的计算，运算量大，速度较慢

2.存在非线性饱和区，容易在反向传播时引起梯度消散（可用batch normalization的方法缓解 ）

3.输出都是正值，会导致梯度下降出现锯齿形晃动，降低梯度下降速度（可用batch normalization 的方法缓解）

 

关于出现锯齿形晃动的原因，是因为在用梯度下降做反向传播时，损失函数对参数的求导会有一项是z=w*x+b对w的求导，得到的结果就是x，如果上层输出全是正值，那么求得的梯度符号就全为正或全为负，正负值取决于剩下的项，这样就会使梯度更新的方向为（+，+）或（-，-）（对于参数是二元的情况），这样的话如果正确的梯度下降方向是（+，-）的话，参数在更新时就不会沿着正确的方向更新，而是以锯齿状逼近最优解，使算法收敛速度变慢。其图形化表示如下图所示：

 

 2.tanh —— 

 

tanh是1991年提出的激活函数，也是最早的激活函数之一，图像如下图：

tanh的优点

1. 函数光滑可微，导数计算方便

2. 输出值 0 中心对称，稳定在 [-1, 1]

3. 具有在 0 附近梯度较大，有利于区别小的特征差异

tanh的缺点

1. 涉及指数的计算，运算量大，速度较慢

2. 存在非线性饱和区，容易在反向传播时引起梯度消散，但比 sigmoid 要轻（sigmoid的导数最大是0.25，tanh是1）

 

3.Relu —— 

从提出到现在最常用的激活函数之一。

Relu的优点

1. 解决了梯度消散问题 ( 在正区间 )

2. 计算简单且速度非常快，只需要判断输入是否大于 0

3. 收敛速度远快于 sigmoid 和 tanh

Relu的缺点

1. ReLU 的输出都是非负值

2. 某些神经元可能永远不会被激活，相应的参数永远不能被更新（两种原因导致：不幸的参数初始化和学习率较高导致在训练过程中参数更新太大越过最优值落入死亡区）（解决办法：使用Xavier初始化方法，使用较小的学习率）

 

 尽管存在上述两个缺点，relu仍是目前最常用的激活函数，在做神经网络应用时仍推荐优先尝试

 

 

 4. Relu的变种——Softplus, Leaky Relu, RRelu, PRelu, Elu, Selu

 

由于relu的良好特性，针对它的缺点，人们提出了很多它的变种：

softplus和relu的图像对比，softplus可以看作relu的平滑版：

softplus是2010年提出的激活函数，根据神经科学家的相关研究，Softplus和ReLu与脑神经元激活频率函数有神似的地方。也就是说，相比于早期的激活函数，Softplus和ReLu更加接近脑神经元的激活模型，而神经网络正是基于脑神经科学发展而来，这两个激活函数的应用促成了神经网络研究的新浪潮。

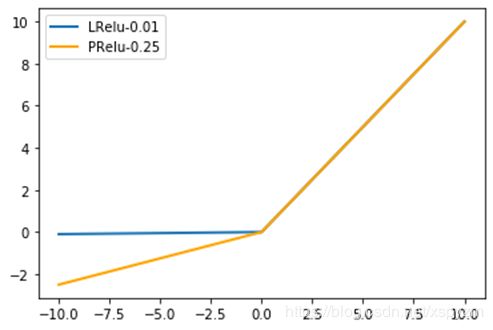
lrelu和prelu的对比：

lrelu、rrelu、prelu形式相差不大，这里只对prelu做说明，prelu在提出的论文中是将参数初始化为0.25，在梯度下降时用了momentum方法进行优化。

PRelu的特点

1. Relu 的所有优点

2. 解决了 Dead ReLU 问题

3. 引入超参数，但只增加了一点点网络计算量和过拟合的危险性

4. 首次使 CNN 在 ImageNet 上的识别率超过人类

ELU的特点

1. Relu 的基本所有优点但计算量稍大

2. 解决了 Dead ReLU 问题

3. 输出的均值接近 0

4. 在 5 层以上的网络上学习速度比 Relu 更快，泛化能力更强

SELU的特点

1. 当选取 =1.0506 ， =1.67326 时，输出的期望为 0 ，方差为 1 ，即模型具有自归一化属性

2. 加速模型收敛速度

5.Maxout —— 

Maxout是深度学习网络中的一层网络，就像池化层、卷积层一样等，我们可以把Maxout 看成是网络的激活函数层，为便于理解，以下是第i层有两个神经元，第i+1层有一个神经元，Maxout层参数k设置为5的情况：

maxout相当于把原来的激活函数换成了一层隐藏层，在隐藏层上训练自己的参数w和b然后将z=wx+b最大的那个值输出

与常规激活函数不同的是，maxout是一个可学习的分段线性函数。

任何一个凸函数，都可以由线性分段函数进行逼近近似。其实我们可以把以前所学到的激活函数：ReLU、abs激活函数，看成是分成两段的线性函数，如下示意图所示：

拿最后一个图来说，如果真正的非线性函数形式是平方函数，那么在k设置为5的情况下，maxout会用5条直线去逼近它，当给出x后，maxout的输出就是在x处5条直线函数值最接近平方函数的那个。

实验结果表明Maxout与Dropout组合使用可以发挥比较好的效果。

Maxout的优点

1. 拟合能力非常强，可以拟合任意的凸函数。

2. 具有 ReLU 的所有优点，线性、不饱和性。

3. 不存在 Dead ReLU 问题

Maxout的缺点

1. 参数个数会成 k 倍增加，大大加大了计算量

6.Swish —— f(x)=x⋅sigmoid(βx)    β是常数或可训练的参数

swish是2017年由谷歌提出的激活函数，从其函数表达式我们可以看出，当β=0时，swish=x/2，当β趋于无穷时，sigmoid(βx)=0或1，swish变成relu，所以swish可以看作是介于线性函数和relu之间的平滑函数。

β取不同值的图像如下所示：

在谷歌的论文中，swish在大型数据集和各种神经网络中相对于其他激活函数表现出了绝对的优势，这意味着我们以后在实践时不再需要测试很多激活函数了。

Swish的特点

1. 无上界有下界、平滑、非单调

2. 在深层模型上的效果优于其他激活函数。仅仅使用 Swish 单元替换 ReLU 就能把 ImageNet 上的 top-1 分类准确率提高 0.9% ， Inception- ResNet -v 的分类准确率提高 0.6% 。

3. 计算速度比 Relu 稍慢

4. 当 β =1 时，激活后的数据分布接近 0 对称

7.Mish —— f(x)=x⋅tanh(ln(1+e^x )) 

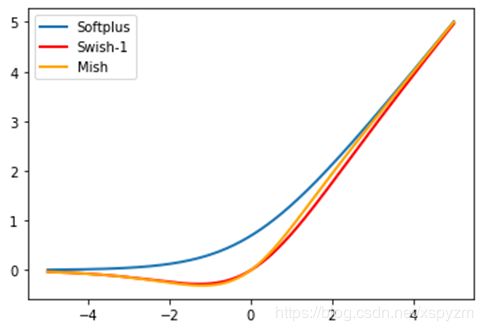
mish是2019年刚提出的激活函数，其图像与softplus和swish-1的对比如下：

我们可以看到，mish与swish-1的差别甚微，仅在原点周围略有不同。但论文指出，当网络层数增加时，尤其到了16层以后，relu的精度迅速下降，其次是swish，而mish仍然保持着良好的表现，这微小的差距在经过深层网络之后被放大，展现出了较大的差距。另外mish还刷新了12个排行榜记录。

Mish的特点

 

1. Mish 在训练稳定性、平均准确率、峰值准确率等方面都有了全面的提高

2. 复杂度只稍微增加了一点 (V100 GPU 和 Mish ，相对于 ReLU ，每 epoch 增加大约 1 秒 )

 

 四、一些不常用的激活函数

前两个分别是浙大和南京邮电的两位学生提出的激活函数，其图像类似于relu的变种，最后一个函数同样是一个没多少人知道的激活函数——惩罚双曲正切函数，但在今年，德国某大学发表了一篇论文，论文中用了21种激活函数分别在NLP任务上做实验，实验意外的发现惩罚双曲正切函数在各个任务上都表现良好且稳定。

五、一些表现良好的激活函数图像比较