《强化学习Sutton》读书笔记（三）——动态规划（Dynamic Programming）

此为《强化学习》第四章。

策略评估

策略评估 (Policy Evaluation) 首先考虑已知策略 π(a|s) π ( a | s ) ，求解 vπ(s) v π ( s ) 。根据上一节中状态值函数的Bellman等式，有

vπ(s)=∑aπ(a|s)∑s′∑rp(s′,r|s,a)[r+γvπ(s′)] v π ( s ) = ∑ a π ( a | s ) ∑ s ′ ∑ r p ( s ′ , r | s , a ) [ r + γ v π ( s ′ ) ]

如果我们已知整个环境，那么对每个状态 s s 都可以列出一条这样的方程，联立，即可解出 vπ(s) v π ( s ) 。

此外，我们也可以使用迭代法求解。首先，随机在每个状态上给定一个值函数 v0(s) v 0 ( s ) ，然后按照如下的迭代进行：

vk+1(s)=∑aπ(a|s)∑s′∑rp(s′,r|s,a)[r+γvk(s′)] v k + 1 ( s ) = ∑ a π ( a | s ) ∑ s ′ ∑ r p ( s ′ , r | s , a ) [ r + γ v k ( s ′ ) ]

显然， vk=vπ v k = v π 是上述方程的不动点。不加证明的给出，随着迭代的进行， vk v k 可以收敛到 vπ v π 。此算法被称为迭代策略评估 (Iterative Policy Evaluation) 。书中给出了迭代策略评估的伪代码，如下图。

策略改良

已知策略 π π ，并在策略评估中计算得到了各个状态 s s 的值函数 v(s) v ( s ) ，然后考虑改良策略，提升值函数。策略改良 (Policy Improvement) 的方法非常直观，在状态 s s 下，如果每个行为都固定地指向唯一的下一个状态 s′ s ′ ，那么基于贪心算法，直接选择 v(s′) v ( s ′ ) 最大的行为即可。更一般地，如果每个行为都符合一个概率分布到下一个状态 St+1 S t + 1 ，得到奖励 Rt+1 R t + 1 ，那么也基于贪心算法，选择一个期望最大的行为作为策略即可。它的数学描述如下：

π′(s)=argmaxaqπ(s,a)=argmaxaE[Rt+1+γvπ(St+1)|St=s,At=a]=argmaxa∑s′∑rp(s′,a|s,a)[r+γvπ(s′)] π ′ ( s ) = arg ⁡ max a q π ( s , a ) = arg ⁡ max a E [ R t + 1 + γ v π ( S t + 1 ) | S t = s , A t = a ] = arg ⁡ max a ∑ s ′ ∑ r p ( s ′ , a | s , a ) [ r + γ v π ( s ′ ) ]

可以证明（详见书本）， vπ′(s)≥vπ(s) v π ′ ( s ) ≥ v π ( s ) 。如果 vπ′(s)=vπ(s) v π ′ ( s ) = v π ( s ) ，则根据最优Bellman等式，那么 π π 和 π′ π ′ 都是最优策略。

策略迭代

由前面两节，很容易看到，首先随机给出一个策略 π0 π 0 ，然后进行策略评估得到一组值函数 vπ0(s) v π 0 ( s ) ，再策略改良得到一个更优的策略 π1 π 1 ，……，反复迭代即可使策略越来越优，趋向于最优策略，如下图所示。

其中， E E 代表策略评估， I I 代表策略改良。这样的强化学习算法被称为策略迭代 (Policy Iteration) 。它的伪代码如下图。

值迭代

策略迭代一个主要的问题在于策略评估，无论解方程法还是迭代法都会比较耗时。一种替代方案为值迭代 (Value Iteration) ，过程如下：

vk+1(s)=maxaqk(s,a)=maxaE[Rt+1+γvk(St+1)|St=s,At=a]=maxa∑s′∑rp(s′,a|s,a)[r+γvk(s′)] v k + 1 ( s ) = max a q k ( s , a ) = max a E [ R t + 1 + γ v k ( S t + 1 ) | S t = s , A t = a ] = max a ∑ s ′ ∑ r p ( s ′ , a | s , a ) [ r + γ v k ( s ′ ) ]

它的式子和策略改良非常类似，唯一的不同点在于，策略改良寻找了当前状态值函数的更优策略，而值迭代不求策略，而是直接用当前的状态值函数来影响附近状态的值函数。从这个角度出发，值函数省略了策略评估的步骤，不再需要对一个策略求出它具体的状态值函数。

另一个思考的角度是，值迭代表达式和Bellman等式几乎一样，因此也是一种不动点迭代的方法。两种思路的证明过程略，但直观上都还好理解。值迭代的伪代码如下。

异步动态规划

当前我们讨论的策略迭代和值迭代都是同步的，即我们先保存好当前迭代的值函数，然后使用它们求解下一迭代的值函数。但有时，状态空间非常庞大，以至于遍历是一件比较耗时的操作。异步动态规划在原来的值函数上直接修改，且顺序不定（可能出现某个状态迭代过好几轮，而另一状态仍未迭代的情况）。这样的算法节省了空间，同时为实时交互提供了可能。然而，异步动态规划可能会提升迭代效率，也可能会降低迭代效率，这是无法保证的。

泛化的策略迭代

策略迭代通常分为两步，一是从当前的策略得到值函数（策略评估），二是从当前的值函数按照贪心算法得到更好的策略（策略改良）。这两步交替进行，比如策略迭代法所做的那样。但这不是必须的，我们不需要等上一步完全结束后再进行下一步。比如在值迭代中，策略评估只进行了一小步，我们就立刻开始进行策略改良。在异步方法中，策略评估和改良更加耦合和细化。

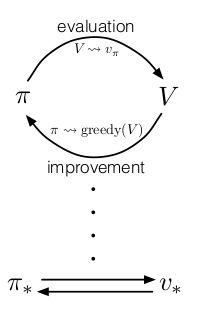
但无论如何，它们的思路都是类似的，即基于策略评估和策略迭代。抛开不同方法具体的实现方式不同，它们都可以简单地用下图进行概括：

动态规划的效率

动态规划可能不适合用来解规模非常大的问题，但和其他求解MDP的方法相比，它还是高效的。在最差情况下，DP也能够在多项式复杂度内找到最优策略。有时，DP被认为会受限于维度诅咒 (Curse of Dimension) ，因为状态的数量可能会随状态变量数量的增加而呈指数级增长。但作者认为，这是问题本身复杂度提升，不能说明DP不是一个好方法。即使对于大规模的问题，DP相比于直接搜索或者线性规划仍然有很大的优势。

在实践中，DP可以处理百万级状态数量的问题。策略迭代和值迭代都被广泛使用，并且各有优劣。通常这些方法都能比它们理论最低收敛速度收敛得快，尤其当它们从一个比较好的起始点出发开始迭代。对于更大规模的问题，异步方法将更加合适。

参考文献

《Reinforcement Learning: An Introduction (second edition)》Richard S. Sutton and Andrew G. Barto

上一篇：《强化学习Sutton》读书笔记（二）——有限马尔科夫决策过程（Finite Markov Decision Processes）
下一篇：《强化学习Sutton》读书笔记（四）——蒙特卡洛方法（Monte Carlo Methods）