线性方程组6种数值解法的对比研究

线性方程组数值解法实验研究

一、实验目的

熟悉求解线性方程组的有关理论和方法；会编写Gauss消去法、LU分解法、Jacobi迭代法、Gauss-Seidel迭代法、超松弛(SOR)迭代法及共轭梯度法的程序；通过实际计算，进一步了解各种方法的优缺点，选择合适的数值方法。

二、实验内容

1. 编程实现Gauss消去法、LU分解法，并用这两种方法求解线性方程组：
   
   ⎧⎩⎨⎪⎪x1+2x2−2x3=7x1+x2+x3=22x1+2x2+x3=5(1)
2. 编写Jacobi迭代法、高斯-赛德尔迭代法程序，并用其求解以下84阶线性方程组，并指出各迭代法是否收敛？实验结果说明什么问题？
   
   ⎛⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜6816816⋱1⋱8⋱6816816⎞⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎛⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜x1x2x3⋮x82x83x84⎞⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟=⎛⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜71515⋮151514⎞⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟(2)
3. 编写超松弛(SOR)迭代法程序，并用其求解以下4阶方程组，并分析超松弛因子 对SOR收敛性的影响。实验结果说明了什么问题？
   
   ⎛⎝⎜⎜⎜13.422−13.42200012.252−12.25200012.377−12.37700011.797⎞⎠⎟⎟⎟⎛⎝⎜⎜⎜x1x2x3x4⎞⎠⎟⎟⎟=⎛⎝⎜⎜⎜750.530010230⎞⎠⎟⎟⎟(3)
4. 编写共轭梯度法程序 ，并用其求解问题(1)(2)(3)中的方程组，并求出共轭梯度法在这三种问题下的收敛速度，列出详细的分析过程。

三、实验结果分析

1. Gauss消去法与LU分解法求解线性方程组

根据线性方程组公式(1)可得，系数矩阵 A 和常数向量 b

A=⎛⎝⎜112212−211⎞⎠⎟,b=⎛⎝⎜725⎞⎠⎟

假设

x=[x1x2x3]T

由此可得

Ax=b

其中，根据矩阵 A 的初等行变换，可以得到矩阵 A 的秩为3，因此，该线性方程组具有唯一确定解。Gauss消去法和LU分解法都可以得到解。其结果如表1所示。

表1 实验1的结果

方法	x	计算误差( >2.22E−16 )
Gauss消去法	[12−1]T	0
LU分解法	[12−1]T	0

2. Jacobi迭代法与Gauss-Seidel迭代法求解84阶线性方程组

根据公式(2)，建立线性方程组标准方程

Ax=b

式中

A=⎛⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜6816816⋱1⋱8⋱6816816⎞⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟,b=⎛⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜71515⋮151514⎞⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟

x=(x1x2x3⋯x82x83x84)T

基于迭代公式

x(k+1)=Gx(k)+f(4)

将系数矩阵 A 分解成对角矩阵和上(下)三角矩阵的组合，即

A=D−L−U

其中

D=diag(666⋯666)

L=−⎛⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜08080⋱⋱808080⎞⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟

U=−⎛⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜010101⋱⋱01010⎞⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟

根据问题的特殊性，很容易发现该问题的解为

x∗=(111⋯111)

由于常系数矩阵 A 不是满秩矩阵，因此该问题存在多个解。

2.1 Jacobi迭代法

Jacobi迭代法的迭代公式为

Dx(k+1)=(L+U)x(k)+b(5)

将公式(5)转化为公式(4)的形式，则可得

G=D−1(L+U)

f=D−1b

接下来分析该迭代法时候收敛，计算矩阵 G 的谱半径 ρ(G)

ρ(G)=max{|λi||λi∈λ,Aε=λε}=1.1195>1

因此，Jacobi迭代法对该问题不收敛，无法求解。

2.2 Gauss-Seidel迭代法

Gauss-Seidel迭代法的迭代公式为

(D−L)x(k+1)=Ux(k)+b(6)

将公式(6)转化为公式(4)的形式，则可得

G=(D−L)−1U

f=(D−L)−1b

接下来分析该迭代法时候收敛，计算矩阵 G 的谱半径 ρ(G)

ρ(G)=max{|λi||λi∈λ,Aε=λε}=0.88747<1

因此，Gauss-Seidel迭代法可以求解该问题，计算结果如表2所示。

表2 问题2的Gauss-Seidel迭代法计算结果

迭代次数	允许误差	实际误差
598	1E-4	9.4250E-5

以上2种方法求解该问题时，发现Jacobi迭代法不收敛，Gauss-Seidel迭代法收敛，在允许精度为1E-4的情况下，迭代次数为598次，可见Gauss-Seidel迭代法在求解该线性方程组时，收敛速度不佳。

3. 超松弛(SOR)迭代法

在Gauss-Seidel迭代法的基础上，为获得更快的收敛效果，在修正量前乘以一个修正系数 ω ，即得到逐次超松弛迭代法，简称SOR迭代法，其中 ω 为松弛因子。SOR迭代法的迭代格式为

x(k+1)=x(k)+ωD−1(Lx(k+1)+Ux(k)−Dx(k)+b)(7)

将公式(7)转化为公式(4)的形式，即

G=(D−ωL)−1[(1−ω)D+ωU]x(k)

f=ω(D−ωL)−1

接下来分析该迭代法时候收敛，计算矩阵 G 的谱半径 ρ(G)

ρ(G)=max{|λi||λi∈λ,Aε=λε}

则SOR迭代法的谱半径 ρ(G) 和松弛因子 ω 相关，因此，我们讨论 ω 和谱半径及迭代次数的关系。采用问题(3)的线性方程组，分析松弛因子 ω 对收敛速度即谱半径 ρ(G) 的影响，其中 ω∈(0,2) ，结果如图1所示。
系数矩阵A和常数向量b分别为

A=⎛⎝⎜⎜⎜13.422−13.42200012.252−12.25200012.377−12.37700011.797⎞⎠⎟⎟⎟,b=⎛⎝⎜⎜⎜750.530010230⎞⎠⎟⎟⎟

由计算结果可得，当 ω=1 时，迭代次数最小，其迭代次数为1。图1描述了随松弛因子变化时，曲率半径和迭代次数的变化。由此，我们发现，在这个算例下，迭代次数和曲率半径呈正相关，曲率半径最小的时候，迭代次数最小。

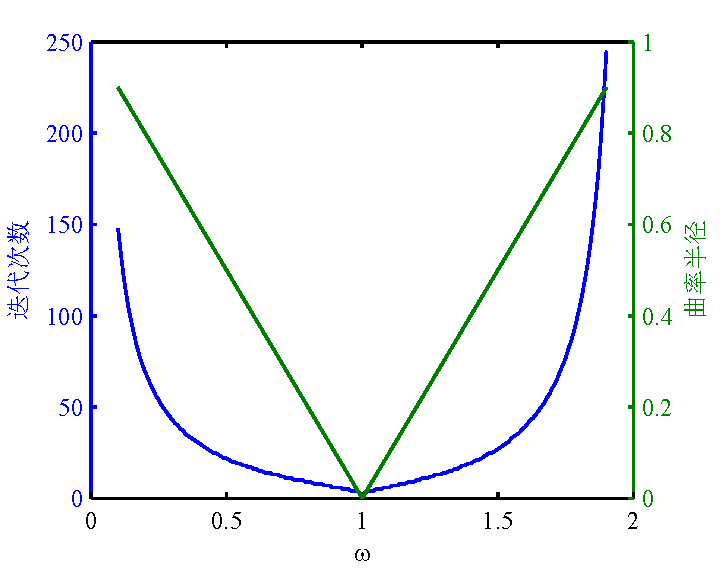
图1 问题3的SOR迭代法计算结果(计算精度为1E-4)

4. 共轭梯度法

共轭梯度法与之前的迭代法不同，它属于不定常迭代法，用于求解对称正对线性方程组，其本质上是一种变分方法。
共轭梯度法的迭代方程为

x(k+1)=x(k)+αkp(k)

其中
αk=∥∥r(k)∥∥22/(Ap(k),p(k)) , p(k) 为第 k 次迭代过程中的搜索方向，它与梯度方向 r(k) 相关，即

p(k+1)=r(k+1)+βkp(k)

其中

r(k+1)=r(k)−αAp(k)

βk=∥∥r(k+1)∥∥22/∥∥r(k)∥∥22

当 ∥βk∥<TOL 时，则迭代结束，其中 TOL 为允许误差。
对于初始解，共轭迭代法要求其为最速下降方向，这可以保证所有的迭代过程中的 x(k) 都是共轭的，且具有较快地收敛速度。
针对问题(1)(2)(3)中的算例，共轭迭代法首先要求对系数矩阵作对角化处理，即

b=ATb,A=ATA

其计算结果如表3所示。

表3 问题1,2,3的共轭迭代法计算结果

问题序号	迭代次数	计算误差	允许误差
1	2	7.9422E-5
2	11	8.8953E-5	1E-4
3	4	1.9327E-5

由表3所得，共轭迭代法在问题(1)(2)(3)中的线性方程组求解上具有较好的收敛效果，尤其对问题(2)中的大型稀疏矩阵上，其收敛效果明显高于Gauss-Seidel迭代法。

四、实验结论

线性方程组的直接求法，Gauss消去法和LU分解法在维度较小的非病态问题上，具有良好的效果。这两种算法理论上的复杂度为 O(n3) ，使其能有效地求出低维非病态线性方程组的精确解，但在髙维度或病态的线性方程组问题上出现无法在有限时间内收敛或无法求解的情况。
线性方程组的迭代求法，Jacobi迭代法、Gauss-Seidel迭代法、超松弛(SOR)迭代法和共轭梯度法针对大型稀疏矩阵（如问题(2)的84阶线性方程组）表现出不同的效果。Jacobi迭代法的不收敛、Gauss-Seidel迭代法的极大的迭代次数以及共轭梯度法较优的计算结果，表明了这些迭代法不同的计算特性。SOR迭代法的松弛因子 ω 对算法的收敛性影响较大，同时，在问题(3)的分析与求解过程中，我们发现谱半径与SOR迭代法呈正相关特性。
基于以上实验结果，我们得到以下结论：
1. 直接求法在一般问题，维数较小下(系数矩阵的秩小于100)，非常实用。
2. 迭代法的收敛性在不同问题反映出的现象差异很大。
3. 采用Jacobi迭代法、Gauss-Seidel迭代法求解大型稀疏矩阵，收敛性难以保证，而共轭迭代法收敛极好。
4. 超松弛迭代法的收敛性受松弛因子影响，并可能存在最优的松弛因子，使其收敛速度最快。

五、实验程序

所有程序都在MATLAB(R2012b)平台上实现。

1. Gauss 消去法

源代码

function [rankA, rankB, N, X] = CNumbericGauss(A, b)
% 调用格式: [rankA, rankB, N, X] = CNumbericGauss(A, b)
%
% 作者: 王瑞
% 时间: 2015.10.27 17:12 - 20.12
% 版本: Version 1.0
%
% 任务: 高斯消去法求解线性方程组的解 Ax = b, 换主元的高斯消去法, 取最邻近非 0 首项
%
% 输入: A = 系数矩阵, 方阵
%       b = 常系数向量, 行向量
%
% 输出: rankA = 系数矩阵 A 的秩
%       rankB = 增广矩阵 B 的秩, 其中 B = [A|b]
%       N = 方程组未知量个数
%       X = 方程组的解向量
% 

B = [A b];
rankA = rank(A);
rankB = rank(B);
N = length(b);
X = zeros(size(b));
if rankA ~= rankB
    disp('None: 矩阵 A 的秩不等于 [A b] 的秩， 无解！');
    return ;
end
if rankA < N
    disp(['Waring: 矩阵的秩小于' num2str(N) '，存在无穷多解。']);
    return;
end
if N == 1
    disp('别闹，用手算的。');
    return;
end
%% Gauss 消去法
if rankA == N
    disp(['Good: 矩阵的秩为' num2str(N) '，存在唯一解。']);
    for i = 1 : N
        if abs(B(i, i)) <= eps
            B(i, i) = 0;
            [flag, j] = max(abs(B(i:N, i)));
            j = j + i -1;
            temp = B(i, :);
            B(i, :) = B(j, :);
            B(j, :) = temp;

            if abs(flag) <= eps        % 无非 0 首项判定
                disp('这里出现了一个 Error，首项极小！');
                return;
            end
        end
        B(i, :) = B(i, :)/B(i, i);
        for j = i+1 : N         % Gauss 消去
            B(j, :) = B(j, :) - B(j, i)*B(i, :);
        end
    end
    for i = N : -1 : 1          % Gauss 回代求解
        if i == N
            X(i) = B(i, N+1)/B(i, N);
        else
            X(i) = (B(i, N+1) - B(i, i+1:N)*X(i+1:N)) / B(i, i);
        end
    end
end
end

2. LU分解法

源代码

function [rankA, rankB, N, X] = CNumbericLU(A, b)
% 调用格式: [rankA, rankB, N, X] = CNumbericLU(A, b)
%
% 作者: 王瑞
% 时间: 2015.10.27 20:14 - 21:37
% 版本: Version 1.0
%
% 任务: 选主元的三角分解法求解线性方程组的解 Ax = b, LU 法
%
% 输入: A = 系数矩阵, 方阵
%       b = 常系数向量, 行向量
%
% 输出: rankA = 系数矩阵 A 的秩
%       rankB = 增广矩阵 B 的秩, 其中 B = [A|b]
%       N = 方程组未知量个数
%       X = 方程组的解向量
% 
B = [A b];
rankA = rank(A);
rankB = rank(B);
N = length(b);
X = zeros(size(b));
if rankA ~= rankB
    disp('None: 矩阵 A 的秩不等于 [A b] 的秩， 无解！');
    return ;
elseif rankA ~= N
    disp(['Waring: 矩阵的秩小于' num2str(N) '，存在无穷多解。']);
    return;
end
if rankA == 1
    disp('别闹，用手算的。');
    return;
end
disp(['Good: 矩阵的秩为' num2str(N) '，存在唯一解。']);
%% 求 L U P [核心]
[L, U, P] = lu(A);
b = P*b;
%% 求 y
y = zeros(size(b));
for i = 1 : N
    if i == 1
        y(1) = b(1);
    else
        y(i) = b(i) - L(i, 1:i-1)*y(1:i-1);
    end
end
%% 求 X
for i = N : -1 : 1
    if i == N
        X(i) = y(i) / U(i, i);
    else
        X(i) = (y(i) - U(i, i+1:N)*X(i+1:N)) / U(i, i);
    end
end
end

3. Jacobi迭代法

源代码

function [rankA, rankB, N, X, ite, tol] = CNumbericJacobiIteration(A, b, TOL, ITE, initX)
% 调用格式: [rankA, rankB, N, X, ite, tol] = CNumbericJacobiIteration(A, b, initX, TOL, ITE, initX)
%           [rankA, rankB, N, X, ite, tol] = CNumbericJacobiIteration(A, b, initX, TOL, ITE)
%
% 作者: 王瑞
% 时间: 2015.10.27 21:40; 2015.10.28 13:37 - 15:00
% 版本: Version 1.0
%
% 任务: Jacobi迭代法求解线性方程组的解 Ax = b
%       构建 x(k+1) = Bx(k) + f
%       B = E - D^-1*A = D^-1*(L+U), f = D^-1*b;
%
% 输入: A = 系数矩阵, 方阵
%       b = 常系数向量, 行向量
%       initX = 初始解
%       ITE = 迭代次数上限
%       TOL = 解的精度(范数)
%
% 输出: rankA = 系数矩阵 A 的秩
%       rankB = 增广矩阵 B 的秩, 其中 B = [A|b]
%       N = 方程组未知量个数
%       X = 方程组的解向量
%       ite = 求解的迭代次数
%       tol = 实际误差
% 
if nargin == 5
    X = initX;
elseif nargin == 4
    X = zeros(size(b));
end

B = [A, b];
rankA = rank(A);
rankB = rank(B);
N = length(b);
ite = 0;
tol = inf;
if rankA ~= rankB
    disp('None: 矩阵 A 的秩不等于 [A b] 的秩， 无解！');
    return ;
elseif rankA ~= N
    disp(['Waring: 矩阵的秩小于' num2str(N) '[' num2str(rankA) ']''，存在无穷多解。']);
end
if rankA == 1
    disp('别闹，用手算的。');
    return;
end
if rankA == N
    disp(['Good: 矩阵的秩为' num2str(N) '，存在唯一解。']);
end
%% B0, f
D = diag(A);
L = (-1) * tril(A, -1);
U = (-1) * triu(A, 1);
invD = diag(1./D);
B0 = invD*(L+U);
f = invD*b;
R = max(abs(eig(B0)));              % 谱半径，收敛判定
if R >= 1
    disp(['Error: 谱半径 R = ' num2str(R) '，大于等于 1，算法不收敛。']);
    return;
end
%% Jacobi 迭代
while ite < ITE
    ite = ite + 1;
    X = B0*X + f;
    tol = norm(b - A*X) / norm(b);
    if tol < TOL
        disp('Excatly: 求得解。');
        break;
    end
end
if ite > ITE
    disp(['Message: 在 ' num2str(ITE) ' 次迭代过程中，无法求得解，'...
        '建议增大总的迭代次数 或者 分析算法的收敛性。']);
end
end

4. Gauss-Seidel迭代法

源代码

function [rankA, rankB, N, X, ite, tol] = CNumbericGaussSeidelIteration(A, b, TOL, ITE, initX)
% 调用格式: [rankA, rankB, N, X, ite, tol] = CNumbericGaussSeidelIteration(A, b, TOL, ITE, initX)
%           [rankA, rankB, N, X, ite, tol] = CNumbericGaussSeidelIteration(A, b, TOL, ITE)
%
% 作者: 王瑞
% 时间: 2015.10.28 14:15 - 15:00
% 版本: Version 1.0
%
% 任务: Gauss-Seidel迭代法求解线性方程组的解 Ax = b
%       构建 x(k+1) = Gx(k) + f
%       G = (D - L)^-1*U, f = (D - L)^-1*b
%
% 输入: A = 系数矩阵, 方阵
%       b = 常系数向量, 行向量
%       initX = 初始解
%       ITE = 迭代次数上限
%       TOL = 解的精度(范数)
%
% 输出: rankA = 系数矩阵 A 的秩
%       rankB = 增广矩阵 B 的秩, 其中 B = [A|b]
%       N = 方程组未知量个数
%       X = 方程组的解向量
%       ite = 求解的迭代次数
%       tol = 实际误差
% 
if nargin == 5
    X = initX;
elseif nargin == 4
    X = zeros(size(b));
end

B = [A, b];
rankA = rank(A);
rankB = rank(B);
N = length(b);
ite = 0;
tol = inf;
if rankA ~= rankB
    disp('None: 矩阵 A 的秩不等于 [A b] 的秩， 无解！');
    return ;
elseif rankA ~= N
    disp(['Waring: 矩阵的秩小于' num2str(N) '[' num2str(rankA) ']''，存在无穷多解。']);
end
if rankA == 1
    disp('别闹，用手算的。');
    return;
end
if rankA == N
    disp(['Good: 矩阵的秩为' num2str(N) '，存在唯一解。']);
end
%% G, f
D = diag(diag(A));
L = (-1) * tril(A, -1);
U = (-1) * triu(A, 1);
invDL = eye(length(b))/(D - L);
G = invDL*U;
f = invDL*b;
R = max(abs(eig(G)));       % 谱半径，收敛判定
if R >= 1
    disp(['Error: 谱半径 R = ' num2str(R) '，大于等于 1，算法不收敛。']);
    return;
end
%% Gauss-Seidel 迭代
while ite < ITE
    ite = ite + 1;
    Xk = X;
    X = G*Xk + f;
    tol = norm(b - A*X) / norm(b);
    if tol < TOL
        disp('Excatly: 求得解。');
        break;
    end
end
if ite > ITE
    disp(['Message: 在 ' num2str(ITE) ' 次迭代过程中，无法求得解，'...
        '建议增大总的迭代次数 或者 分析算法的收敛性。']);
end
end

5. 超松弛(SOR)迭代法

源代码

function [rankA, rankB, N, X, ite, tol] = CNumbericSORIteration(A, b, Omega, TOL, ITE, initX)
% 调用格式: [rankA, rankB, N, X, ite, tol] = CNumbericSORIteration(A, b, Omega, TOL, ITE, initX)
%           [rankA, rankB, N, X, ite, tol] = CNumbericSORIteration(A, b, Omega, TOL, ITE)
%
% 作者: 王瑞
% 时间: 2015.10.28 16:00 - 16:38
% 版本: Version 1.0
%
% 任务: 超松弛(SOR)迭代法求解线性方程组的解 Ax = b
%       构建 x(k+1) = Gx(k) + f
%       G = (D-Omege*L)^-1*[(1-Omega)*D+Omega*U], 
%       f = Omega*(D-Omega*L)^-1*b
%
% 输入: A = 系数矩阵, 方阵
%       b = 常系数向量, 行向量
%       initX = 初始解
%       Omege = 松弛因子 (0, 2)
%       ITE = 迭代次数上限
%       TOL = 解的精度(范数)
%
% 输出: rankA = 系数矩阵 A 的秩
%       rankB = 增广矩阵 B 的秩, 其中 B = [A|b]
%       N = 方程组未知量个数
%       X = 方程组的解向量
%       ite = 求解的迭代次数
%       tol = 实际误差
% 
if nargin == 5
    X = zeros(size(b));
elseif nargin == 6
    X = initX;
end

B = [A, b];
rankA = rank(A);
rankB = rank(B);
N = length(b);
ite = 0;
tol = inf;
if rankA ~= rankB
    disp('None: 矩阵 A 的秩不等于 [A b] 的秩， 无解！');
    return ;
elseif rankA ~= N
    disp(['Waring: 矩阵的秩小于' num2str(N) '[' num2str(rankA) ']''，存在无穷多解。']);
end
if rankA == 1
    disp('别闹，用手算的。');
    return;
end
if rankA == N
    disp(['Good: 矩阵的秩为' num2str(N) '，存在唯一解。']);
end
%% D, L, U
D = diag(diag(A));
L = (-1) * tril(A, -1);
U = (-1) * triu(A, 1);
%% G, f
G = (D - Omega*L)\((1-Omega)*D + Omega*U);
f = (D - Omega*L)\(Omega*b);
R = max(abs(eig(G)));       % 谱半径，收敛判定
if R >= 1
    disp(['Error: 谱半径 R = ' num2str(R) '，大于等于 1，算法不收敛。']);
    return;
end
disp(['R = ' num2str(R)]);
%% SOR 迭代
while ite < ITE
    ite = ite + 1;
    X = G*X + f;
    tol = norm(b - A*X) / norm(b);
    if tol < TOL
        disp('Excatly: 求得解。');
        break;
    end
end
if ite > ITE
    disp(['Message: 在 ' num2str(ITE) ' 次迭代过程中，无法求得解，'...
        '建议增大总的迭代次数 或者 分析算法的收敛性。']);
end
end

6. 共轭梯度法

源代码

function [rankA, rankB, N, X, ite, tol] = CNumbericCGMIteration(A, b, TOL, ITE, initX)
% 调用格式: [rankA, rankB, N, X, ite, tol] = CNumbericCGMIteration(A, b, TOL, ITE, initX)
%           [rankA, rankB, N, X, ite, tol] = CNumbericCGMIteration(A, b, TOL, ITE)
%
% 作者: 王瑞
% 时间: 2015.10.28 16:54 - 19:21
% 版本: Version 1.0
%
% 任务: 共轭梯度法(Conjugate Gradient Method, CGM)迭代法求解线性方程组的解 Ax = b
%       适用于系数矩阵为对称阵的线性方程组(函数内包含矩阵对称化 b = A'*b, A = A'*A)
%       构建 x(k+1) = x(k) + alpha(k)*p(k)
%       等同 MATLAB 内置函数 cgs
%
% 输入: A = 系数矩阵, 方阵
%       b = 常系数向量, 行向量
%       ITE = 迭代次数上限
%       TOL = 解的精度(范数)
%       initX = 初始解
%
% 输出: rankA = 系数矩阵 A 的秩
%       rankB = 增广矩阵 B 的秩, 其中 B = [A|b]
%       N = 方程组未知量个数
%       X = 方程组的解向量
%       ite = 求解的迭代次数
%       tol = 实际误差
% 
if nargin == 5
    X = initX;
elseif nargin == 4
    X = zeros(size(b));
end
%% 解的判定
B = [A, b];
rankA = rank(A);
rankB = rank(B);
N = length(b);
ite = 0;
tol = inf;
if rankA ~= rankB
    disp('None: 矩阵 A 的秩不等于 [A b] 的秩， 无解！');
    return ;
elseif rankA ~= N
    disp(['Waring: 矩阵的秩小于' num2str(N) '[' num2str(rankA) ']''，存在无穷多解。']);
end
if rankA == 1
    disp('别闹，用手算的。');
    return;
end
if rankA == N
    disp(['Good: 矩阵的秩为' num2str(N) '，存在唯一解。']);
end
% 系数矩阵对称，放大 A' 倍
if rank(A-A') ~= 0
    b = A'*b;
    A = A'*A;
end
% GCM 迭代
r = b - A*X;
while ite < ITE
    err = r'*r;
    ite = ite + 1;
    if ite == 1
        p = r;
    else
        beta = err / errold;
        p = r + beta*p;
    end
    Ap = A*p;
    alpha = err / ((Ap)'*p);
    X = X + alpha*p;
    r = r - alpha*Ap;
    errold = err;
    tol = norm(r) / norm(b);
    if tol < TOL
        disp('Excatly: 求得解。');
        break;
    end
end
if ite > ITE
    disp(['Message: 在 ' num2str(ITE) ' 次迭代过程中，无法求得解，'...
        '建议增大总的迭代次数 或者 分析算法的收敛性。']);
end
end