NLP_task3特征选择_点互信息和互信息(求词语关联性)
点互信息和互信息
- 点互信息PMI
机器学习相关文献里面,经常会用到点互信息PMI(Pointwise Mutual Information)这个指标来衡量两个事物之间的相关性(比如两个词)。
关于PMI
PMI, 是互信息(NMI)中的一种特例, 而互信息,是源于信息论中的一个概念,主要用于衡量2个信号的关联程度.
至于PMI,是在文本处理中,用于计算两个词语之间的关联程度.
比起传统的相似度计算, pmi的好处在于,从统计的角度发现词语共现的情况来分析出词语间是否存在语义相关 , 或者主题相关的情况.
其原理很简单,公式如下:
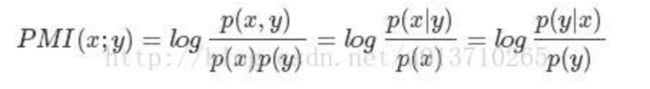
在概率论中,我们知道,如果x跟y不相关,则p(x,y)=p(x)p(y)。二者相关性越大,则p(x, y)就相比于p(x)p(y)越大。
用后面的式子可能更好理解,在y出现的情况下x出现的条件概率p(x|y)除以x本身出现的概率p(x),自然就表示x跟y的相关程度。
这里的log来自于信息论的理论,而且 log 1 = 0 ,也恰恰表明P(x,y) = P(x)P(y),相关性为0,而且log是单调递增函数,所以 “P(x,y) 就相比于 P(x)P(y) 越大,x 和 y 相关性越大” 这一性质也得到保留。
举个自然语言处理中的例子来说,我们想衡量like这个词的极性(正向情感还是负向情感)。我们可以预先挑选一些正向情感的词,
比如good。然后我们算like跟good的PMI。
通常我们可以用一个Co-occurrence Matrix来表示对一个语料库中两个单词出现在同一份文档的统计情况,例如
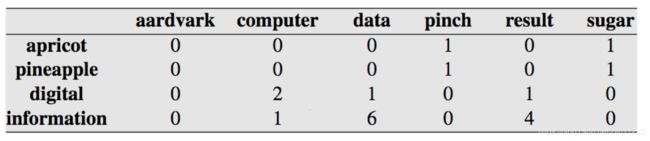
以计算PMI(information,data)为例则有(其中分母上的19是上表所有数值之和):

其他中间结果如下表所示:
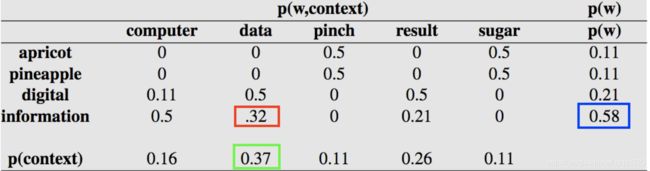
但是从上表中你可能会发现一个问题,那就是你有可能会去计算 log 0 = -inf,即得到一个负无穷。为此人们通常会计算一个PPMI(Positive PMI)来避免出现 -inf,即

- 互信息MI
点互信息PMI其实就是从信息论里面的互信息这个概念里面衍生出来的。
互信息即:
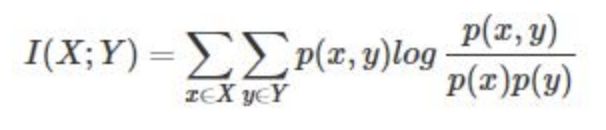
其衡量的是两个随机变量之间的相关性,即一个随机变量中包含的关于另一个随机变量的信息量。所谓的随机变量,即随机试验结
果的量的表示,可以简单理解为按照一个概率分布进行取值的变量,比如随机抽查的一个人的身高就是一个随机变量。
可以看出,互信息其实就是对X和Y的所有可能的取值情况的点互信息PMI的加权和。因此,点互信息这个名字还是很形象的。
- sklearn编程
from sklearn import metrics as mr
mr.mutual_info_score(label,x)
label、x为list或array。
计算x和label的互信息。
参考:https://blog.csdn.net/u013710265/article/details/72848755
https://blog.csdn.net/baimafujinji/article/details/6509820
https://blog.csdn.net/qq_30843221/article/details/50767590