LSI设计(4)FOCR快速最优通道布线及其算法应用和移植
| [摘要]本文提出的快速最优通道布线算法FOCR(Fast Optimal Channel Router)是Kernighan-shweikert-Persky 最优通道布线算法[2]和wada改进布线算法[4]的进一步改进。这些算法的“最优性”意义完全相同,但新算法的执行速度统计地比上述二种法远远为快。 |
1.引 言
通道布线算法是大规模集成电路(LSI)和印刷电路板(PCB)布线设计中广泛应用的一类算法,其特点是采用并行布线方式,因而与串行布线的Lee算法或Highitower算法相比,可以获得高的整体布线质量并容易处理100%布线率问题。
通道布线算法最早由Hashimoto-Stevens[1]提出。他们的算法(左边算法)应用于无约束线网集可保证获得最优介,但应用于约束线网集时结果常不理想。后来Kernighan等人[2]在此基础上应用分支限界法解决了无环约束集的最优布线问题,但算法执行过程较长。Wada[3]则把分支限界法推广到曲干布线[4],提出了一个解决带环约束集100%布线的方案,此外,还着重(占有文章主要篇幅)来介绍两个分支限界过程的加速措施。Wada的两个措施是有益的,但试验表明时间仍可观(见[4]结束语)。本文就是在Wada工作基础上进一步采用了若干加速措施。大量试验表明这些措施是有效的,多数例子在联合应用各种措施后分支限界过程获得了根本简化,且其余的也有不少简化。
2、基本思想
分支限界法的执行过程可分为两个阶段:①在判定树上依次搜索,直到获得一个最优解;②验证此解的最优性,即验证其后一切分支上不再有更优解。显然,要缩短整个算法过程必须同时缩短搜索和验证两个过程。以下是快速最优通道布线算法采用的几个措施。
2.1.线网重排次序 在分支限界过程开始之前,将线网重新排序,使之有利于尽快搜索到最优解和较优解;
2.2.分层次优化 先用一个快速优化算法来产生一个高质量的初始布线,然后再用一般分支限界法进一步优化;
2.3.快速最伏性验证 即除了利用分支限界法外,还使用一种简单但常常十分有效的手段来验证已获得解的最优性;
2.4.用增量法计算界限 即除了首次外,分支限界过程中任何一次求界都是在上一次求界所得数据基础上进行的;
2.5.寻找更精确的界限 寻找一个比Kernighan的动态界限能更精确估算布线需要行数的界限来替代动态界限。
合理的线网排列,优良的初始布线,快速和精确的求界手段都有利于缩短上面所说的第一阶段。而有效的验证手段以及快速精确的求界方法则有助于缩短第二个阶段。实际上,只要不是人为的例子,应用快速最优通道布线算法,在大多数情况下,都能快速获得最优解,并快速验证其最优性,用不到像一般分支限界过程那样进行耗尽式的搜索和验证。
3、加速技巧
以下介绍上述措施的细节。
3.1.线网重排次序
这一措施的目的是让最优解或较优解尽可能排在判定树较早搜到的那些分支上。判定树的结构由分支法确定,Kernighan算法的分支法则就是左边法则 (从上到下或从下到上一行一行地布线,在每一行中,从左到右,每次总是选择当时的最左可布线网布之)。但因划分了zone(重叠区)结构后,最左可布线网一般不是唯一的,因而选择其中哪一个最左可布线网优先布之就有灵活性,这就使判定树的结构在一定程度上可以改变。本措施的具体做法是:在线网的静态界限和约束级别求出之后,在每个zone中,将所有左端位于该zone的线网按照静态界限大小由大到小排列。如果静态界限一致,则按约束级别高低排列。进入分支限界过程后,每次都按这个顺序作为选择最左可布线网的优先顺序。
这一措施可使部分例子只用Hashimoto-Stevens的左边算法就能获得最优解。
3.2.初始布线
可以用任何快速优质通道布线算法来产生初始布线,以下是两个这样的算法。
3.2.1.双边算法(BEA)
见图1。它和左边算法(下记为LEA)一样,采用从上到下或从下到上一行行地布线。但在每一行中,一开始总是选择当时具有最大静态界限和最高约束级别的未布线网布于该行的“中间”。然后,在此线网右边应用左边算法布线直到通道右端;而在此线网左边,则应用与左边算法对称的“右边算法”布线,直到通道左端。同一zone中若有多个线网可选,则在布线之前所作的线网重排(框3,4)能保证优先选择静态界限大的和约束级别高的先布。
双边算法使半数以上的试验例子获得最优解,且其余的也非常接近最优解。
|
|
3.2.2.倒限界分支限界法(RBT)
这是一种限界次序与一般完全颠倒的分支限界法。一般分支限界法为了保证获得解,一开始必须假设一个很宽的限界值,然后让在分支限界过程中实际得到的当前最优解值来不断更新(减少),最终达到最优值(最小值)。
这一过程有时会很长,这就是在判定树上开始都是一些差的解,逐步出现较优解,而最优解排在很后面。考虑到这种可能情况,倒限界法一开始就用一个下界作为界限初值,以达到快速剪支的目的,如果发现实际解都达不到这一数值,则再放宽它,这样由紧到宽来逼近最优解。倒限界法可以用作整体优化,亦可用作局部优化。作为初始布线算法,以下介绍一个逐行应用分支限界法而整个不用的快速部份优化倒限界法。基本思想如下:
一开始,置行数t=1,限界值v=线网全集s的动态界限DB(s)。然后,从上到下(或从下到上)一行一行用左边算法LEA布线。当一行布满时,计算未布集的动态界限DB并判别关系式 DB+t <v 是否成立,若成立,则t = t+1, 去布下一行;否则就按后布先拆的顺序,将t行上位于右边的部分线网拆除 (拆除规则同 Wada [4],详见框图),并用某些最左可布线网继续布满整个t行(选择规则Wada[4],详见框图),再计算未布线网集的DB并判别关系式DB+t<v是否成立,……,这样不断用尚有可能满足关系式的各种可行布线来试布该行,最后有两种可能:①在某种布线下,DB+t<v 式成立,这时就可以t=t+1,去布下一行;②一切可行布线都不能使DB+t<v 成立,这时就取本行各种可行布线中性能最好的一种,即能够使未布的net集的动态界限达到最小值minDB的那种布线作为本行的布线,并令 v = t+minDB ,然后再t=t+1,去布下一行。这样一直下去直到一切线网布完时结束。
图2. 倒限界算法
图2为该算法框图。其中s为已布线网数,z为当前布线起始zone, ZL,ZR为实现Wada加速技巧引进的参数。R是布线标志,1时代表布线(分支),取0为拆线(剪枝);n为线网总数。图3是上述算法与 Kernighan, Wada算法分支限界过程的比较。其中(A)为被布线网集S,DB(S)等于3。(B)为线网约束图。(C)(D)(E)为三个算法的分支限界过程。矢量向右为布线,向左为拆线。一个圆圈代表一次求界,圆内数字为已布行数t与末布线网动态界限DB之和t+DB 。虚线与实线一起构成完整的判定树,如果采用DFS来穷举,就需遍历整个树。(F)为三个算法的共同结果。
由图可知,同样达到最优解(V=3),倒限界法要快得多。自然,作为部分优化算法它不保证都能获得最优解。因此一般地说需要进一步优化。但实际应用中大量例子都能获得最忧解。从理论上则可以证明,只要每次求界都是精确值,则上述算法一定有最优解。
3.3.快速最优性验证
当最优解达到之后,分支限界法本身并不能断定其为最优,必须在判定树上继续搜索直到其后一切分支都考察完毕,发现没有更优解时,才能回头来肯定原来那个解已是最优解。这种方法对于可行解数目很大的所谓“大边缘”问题要消耗大量时间。例如我们曾用一个包含50个线网的无约束集作过试验,采用Wada方法,在布线 50次,求界9次后即得到最优解,而验证其最优性却要在布线和拆线各149624次求界130824次后才完成。快速最优性验证方法很简单:每当得到一个当前最忧解后,就检查它的值是否等于整个集合的动态界限,若相等,则因动态界限必小于等于最优解值,故可断定解已最优,不必再继续分支限界下去。自然,如果最优解值实际小于上述动态界限值,则此快速检验法无效,就必须进行完全的分支限界过程。但这种情况实际是极少遇见的。这一措施 Kernighan 后来已提到,但Wada没有采用。
3.4.增量计算动态界限
动态界限的计算中要求构造一个二维数组 (密度矩阵),它的每一个元素(密度)又必须靠计数来统计得到,因而工作量很大。为了压缩求界工作量,分zone 是明显有益的。另外,我们采用了增量计算法,收效也很可观。增量计算的思想是:除第一次即整个集合的动态界限必须按定义直接计算外,其后任何一个部分集的动态界限都可利用最近一次动态界限计算中所得的数据经过修改得到。具体做法是:每次求界后,保留其密度矩阵和向量序列;当继续布线拆线时,同时也就对密度矩阵进行修改,并把更动线网的最小静态界限k记录下来;当再次求界时,只需利用修改后的密度矩阵对原向量序列中第k个及k以后的那部分向量从算即可。
3.5.更精确的求界方法
Kernighan的动态界限用来估算布线需要的行数,极大多数情况下是完全精确的,但也有例外,图4(A)就是一个。该集合的动态界限为7,而最优布线必须8行(证略)。分析其原因,在于动态界限计算中没有考虑相互重叠的线网在布线过程中带来的新约束关系。例如在图4(B)中,线网①与⑨或②与⑥原来都无约束关系。但因线网①与②相互水平重叠,它们不可能放在同一行,因而在实际布线中,不是①布在②上就是②布在①上。这样也就是说,或者①约束⑨,或者②约束⑥,二者必居甘—。
为了提高精度,新的动态界限要考虑这种情况。对于上例,采用的办法是:从原线网集形成两个新的集合S1与S2,在S1中令①约束②,而S2中②约束①(图4(C),(D)),然后分别计算S1与S2的动态界限 DB(S1),DB(S2), 而新的动态界限NDB(S)=MIN{DB(S1),DB(S2)}。按此方法计算,S的动态界限增加到了8,与最优解值相等了。
必须说明,要完整处理线网重叠引起的垂直约束十分复杂,必须简化才行。这就是只考虑静态界限大的且位于约束图顶部的少数线网,它们的相互重叠最有可能引起新约束。另外,本措施宜选择使用,因对大多数实际问题来说旧界限已精确,无条件用新界限反而使问题复杂化。
.
4、快速最优通道布线算法
将上述措施中的一个或相容的几个加入Kernighan算法或Wada算法中就得到各种不同形式、不同程度的快速最优通道布线算法FOCR ,例如以下形式都是可取的:
4.1 FOCRl = Wada算法 + 增量求界 + 快速最优性验证;
4.2 FOCR2 = FOCRl + 线网预排序 + 部分优化RBT预布线;
4.3 FOCR3 = FOCRl + 线网预排序 + 完全优化的RBT法;
4.4 FOCR4 = FOCRl + 线网预排序 + BEA预布线。
上述算法我们编成FORTRAN程序后曾在PDPll/34上对Kernighan的几个例子[2]以及Deutsch的“困难问题”[4]进行了试验。表1为其部分结果(FOCR3,4结果限于篇幅,略),这里用求界次数作为比较,这与Wada的“Trial”数一致。所用布线顺序对 Kernighan 的例子(1—6列)全为从上到下从左到右;Deutsch例子则因用Wada算法按上顺序运行 2小时后无结果改用了从上到下从右到左顺序。表1中的数据即为该顺序下的结果,所用时间Wada法为2069秒,FOCR2为136秒。对此特例还以Wada本人采用的顺序,即从下到上从左到右,作了试验,结果Wada法为167秒,FOCR2为127秒。值得注意,这一问题用不同顺序布线时困难程度相差甚远! 除了从上到下、从左到右为很困难,其余都不太困难,甚至很不困难。为了减少运行时间,可选择最“容易的”顺序布线(可用左、右边算法试布一下,看哪个结果最好就用那个顺序),并利用不同顺序下的动态界限来选出最精确(大)的值。加人这些措施后我们再试验了一次,结果FOCR2减到36秒(FOCR3为35秒),其中分支限界过程为9秒,其余都化在准备工作上。
表l. 最优算法求界次数比较
|
算 法
|
例 1
|
例 3 上
|
例 3 中
|
例 3 下
|
例 4b
|
例 5
|
Deutsch
|
|
Wada
|
112
|
865
|
461
|
565
|
1241
|
7025
|
12998
|
|
FOCR1
|
24
|
48
|
300
|
220
|
511
|
635
|
12896
|
|
FOCR2
|
11
|
48
|
296
|
17
|
191
|
20
|
836
|
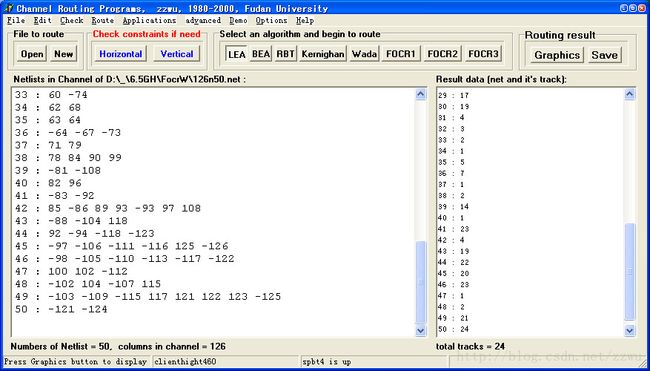
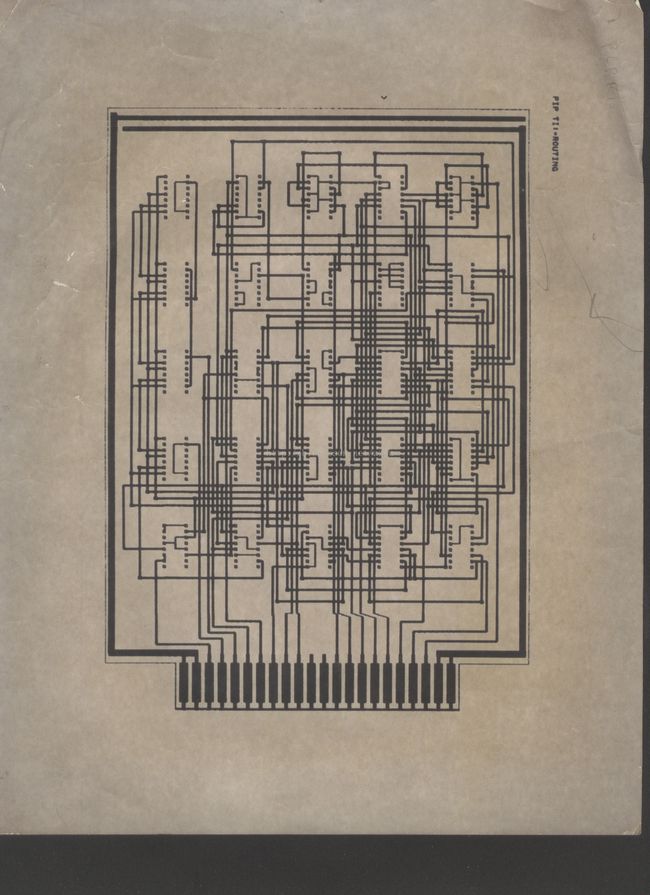
附图 1: FOCR2 对Kernighan例3的布线结果
附图2. FOCR2 对Kernighan例4b的布线结果
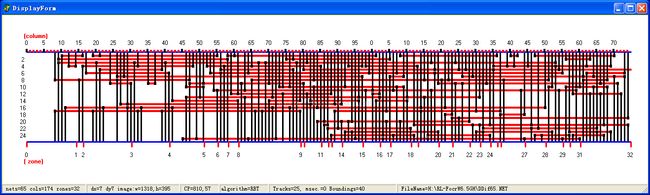
附图3 Deutsch的困难问题
用FOCR2从上到下从右到左布线,在PDP11/34上用CPU
时间136秒,采用自动选择最优布线顺序后降低为36秒
5、结 论
通道布线问题属于NP困难问题,任何有效算法都不能保证结果的最优性,而任何最优算法都不能保证计算的高效性;快速最优算法无疑只是相对地快,统计地快.不排除遇到困难的可能性,但这种可能性已大大减少.事实上,在我们应用快速最优算法进行LSI和PCB的设计实践中还从未遇到过这样的问题,在总数接近200个的通道布线实例[注]中,极大多数是在1—2秒内解决的,最长的也不过十多秒。
作者感谢唐璞山以及原复旦CAD实验室王世民、沙露、陆昉等同志,本算法的某些思想以及程序细节是在这个组80年度讨论班上交流后完善起来的.还感谢计算机房同志的配合和协助。
[注]这些通道布线实例包括:来自文献的不到20个(类似于附图1那样的一个LSI设计就包含7个通道布线);为研究各种通道布线算法而专门设计的通道例子20多个(类似于图3、图4等那样的大大小小通道);为建立完整的LSI多元胞自动布局-布线系统而设计的实例40个(其中一半例子由沙路同学完成设计);为建立完整的PCB自动布局-布线系统而设计的实例30个例子;以及应用PCB 自动布局-布线系统为心脏起搏机测试仪设计5块印刷线路板而进行的通道布线实例75个。
下面附图4和附图5分别是利用LSI多元胞自动布局-布线系统与PCB自动布局-布线系统设计的LSI与PCB。
自动布线系统在进行通道布线前先要进行线网的通道分配,约束环的检测和消除,通道布线完成后则要进行其他参数的优化,包括使布线长度最小,层间穿孔数目最少。
6. 参考文献
[1] A. Hashimoto and J. Stevens,
...“Wire Routing by Optimizing Channel Assignment Within Large Apertures”,
....Proc. of 8th DAC,pp.155-169 (1971).
[2] B. W. Kernighan, D. G. Schweikert and G. Perskey,
....“An Optimal Channel-Routing Algorithm for Polycell Layout of Integrated Circuits”,
....Proc. of 10th DAC, pp 55-59(1973)
[3] D. N. Deutsch,
...“A Dogleg Channel Router”,
... Proc. of 13th DAC, pp 425-433 (1976).
[4] M. M. Wada,
....“A Dogleg “Optimal” Channel Router with Completion Enhancements”,
....Proc. of l8th DAC, pp.762-768 (1981).
其中[2]见:
Fast Optimal Channel Routers
by Z. Z. wu
(Fudan Unversity)
Abstract
This paper presents some optimal channel routers based upon the optimal channel router[2] and the dogleg optimal channel router[4], but improved to various degrees . All these routers have the optimality with the same sense, yet the speed of new algorithm are statistically far much greater than that of the originals .
注:上文是发表在半导体月报1983年4月的文章。由于版面限制,比较浓缩,许多基本概念未介绍,详细可见
http://blog.csdn.net/zzwu/article/details/51166423
程序移植到微机
| 快速最优通道布线算法是我1980、1981年的研究成果,1982年春在昆明全国设计自动化会议上曾提供了一个较完整的介绍。因昆明会议的油印原稿未找到,所以先在这里登载一简化稿。此稿是后来发表在半导体学报的内容。因受5000字的版面限制,某些重要内容,如静态和动态界限的联立递归定义、通道布线算法的推广应用、多种算法的描述和输出结果的比较,等均已被删。待原稿找到后再在这里加以补充。 |
|
本文介绍的软件原来是在DEC公司PDP11-34小型机上用Fortran语言编写,布线结果则是用Tektronix公司4014 高分辨率(4096*3072)黑白显示器上显示后,再用hard copy方法显影到感光纸上,输出质量尚可。但底稿经出版社印刷出版后质量明显下降;现再从刊物上扫描下来,压缩后放到网上,质量就非常差了(见上面附图3)。 |
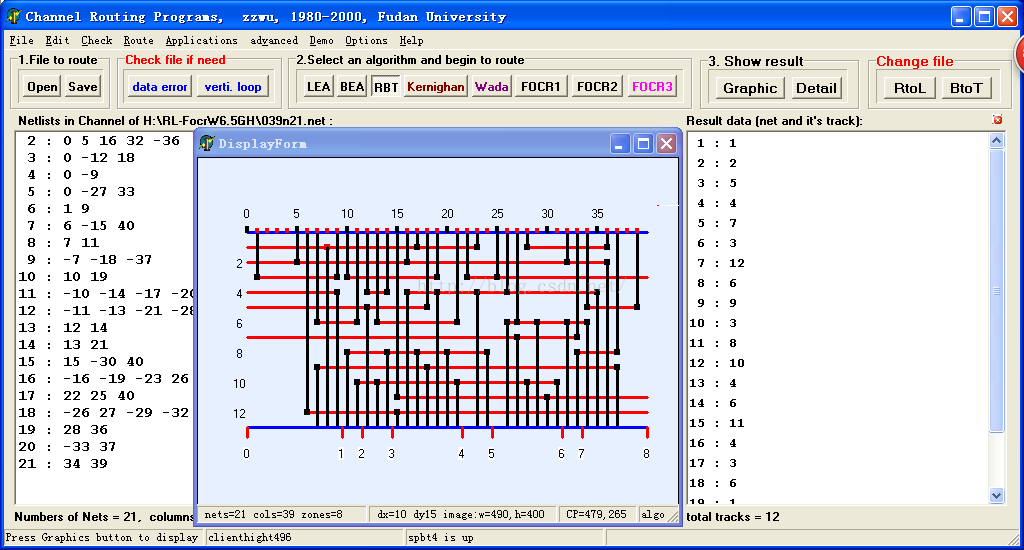
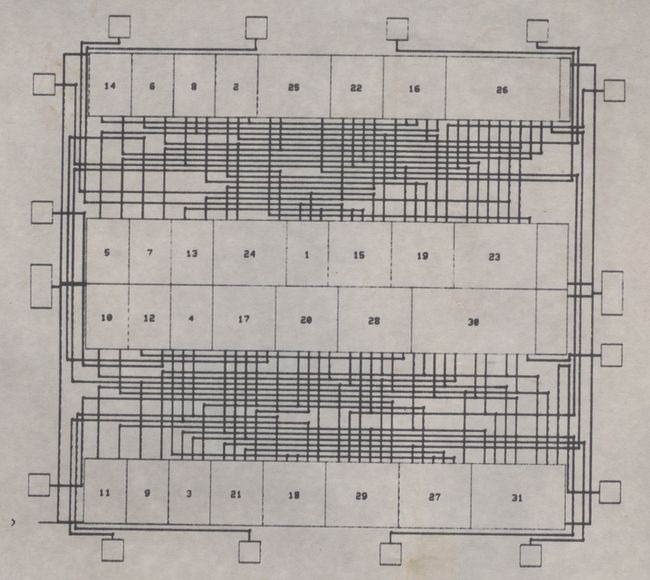
附图5:在奔2机上用左边算法LEA和快速最优通道布线算法FOCR2 对Kernighan例4(a)的布线结果.
左边算法用24行(上),FOCR2只需要17行(下),而所用时间都是0(少于1ms,已无法检测)
(右击上面的图像,选“图片另存为” 再查看图像,可看到设计所得的 1:1 的清晰原图)
附图6 图形实际是在一form中显示,此form可加底色
附图7 dd65,用RBT布线,时间28毫秒
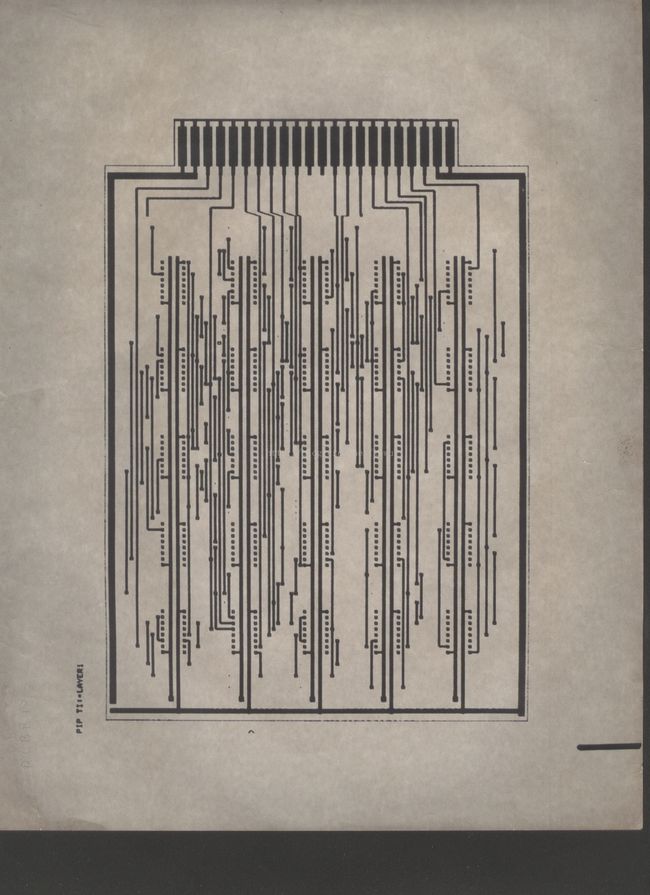
通道布线是整个布线过程的一部分,在用FOCR进行通道布线之前先要进行总体布线,确定大量线网如何分配到各通道,而完成各通道的布线之后要做道孔减少、线长缩短等进一步优化工作。只有在所有这些工作完成、构成一个完整的系统后,才可将其用来进行VLSI自动布线设计或用来进行PCB的自动布线设计。其中VLSI可以用于多元胞(polycells)形式,也可用于门阵列(gate array)形式。我在上世纪80年代已在FOCR基础上,开发了多元胞VLSI布线设计程序与PCB布线设计程序。其中VLSI布线设计程序我们使用了许多次,其中也有不少由我和沙露同学合作完成,沙露负责布局,布好局后再用我的布线程序布线。而PCB布线设计程序实际使用得不多,除了我做试验的以外,只有方祖祥的一位研究生用它来做了几块(4-5块)作为心脏起搏器的测试仪的PCB(不用插件引出) ,也有其他一些单位派人员来学习过,包括四机部,他们对PCB自动布线很感兴趣。门阵列VLSI的布线程序我没有做过,但其原理甚至程序应和PCB布线设计一样,就是有水平和垂直两种通道。下面4图就是当时在PDP机器上设计的一些例子。
以上是心脏起搏器测试仪的一块PCB的正反2个面
salu-1(由沙露同学完成布局,再以FOCR布线)
salu-2(由沙露同学完成布局,再以FOCR布线)
【完】