机器学习(李航统计学方法)之朴素贝叶斯

说明：代码参考的博客链接为(http://www.pkudodo.com)，隆重推荐! 同时也参考了这两位大牛的博客(https://blog.csdn.net/u012162613/article/details/48323777)，
(https://www.letiantian.me/2014-10-12-three-models-of-naive-nayes/)；若文章有错误，希望各位不吝赐教！我会及时修正！

---

目录

---

1、朴素贝叶斯的介绍

常见的分类问题分为两种：第一种是判别方法，即直接学习出特征输出$Y$与特征$X$之间的关系，比如KNN，KD树等，这个关系是决策函数$f(x)$或者是条件分布$P(y/x)$。第二种是生成方法，即直接找出特征输出$Y$与特征$X$之间的联合分布$P(X,Y)$。
朴素贝叶斯分类属于上述的生成方法。它是一个对所有可能性求概率的模型
朴素贝叶斯的直观了解：

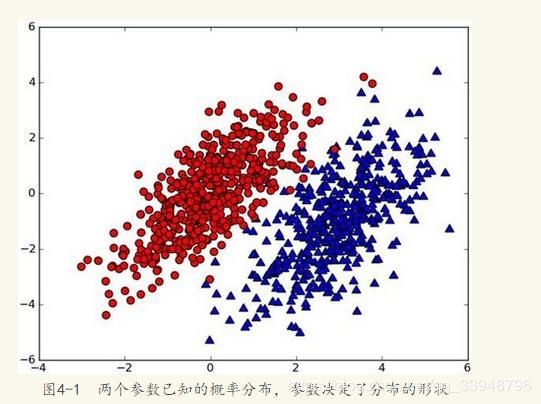
已知一个新的样本点$P(x_0,y_0)$,其属于哪一类未知。假设$P_1(red/x,y)$为样本点属于红色那一类的概率，$P_2(blue/x,y)$为样本点属于蓝色那一类的概率。
选择概率高的一类作为新点的分类，这就是贝叶斯决策理论的核心思想。那么我们可以得出：
$P_1(red/x,y)$ > $P_2(blue/x,y)$;则样本属于红色那一类；
$P_1(red/x,y)$ < $P_2(blue/x,y)$;则样本属于蓝色那一类；
那么如何求$P_1(red/x,y)$ 和 $P_2(blue/x,y)$来实现分类呢？
这时候贝叶斯公式就出场了：

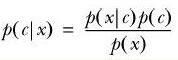
$P(c/x)$表示事件$x$已经发生的前提下，事件$c$发生的概率，叫做事件$x$发生下事件$c$的条件概率。贝叶斯之所以有用，是因为我们在生活中经常遇到这种情况：我们可以很容易直接得出$P(x/c)$，$P(c/x)$则很难直接得出，但我们更关心$P(c/x)$，贝叶斯定理就为我们打通从$P(x/c)$获得$P(c/x)$的道路。
在上面直观了解例子中,$P(x/c)$表示给定数据集的情况下，出现该样本的概率。$P(c/x)$表示给定样本的情况下，属于哪一个数据集的概率。

---

2、朴素贝叶斯的理论基础

朴素贝叶斯基于贝叶斯定理和特征独立假设。

2.1 贝叶斯定理

条件概率：
$P(A|B)$表示事件$B$已经发生的前提下，事件$A$发生的概率，叫做事件$B$发生下事件$A$的条件概率。其基本求解公式为：

贝叶斯定理便是基于条件概率，通过$P(A|B)$来求$P(B|A)$：

上式中的分母$P(A)$,可以根据 全概率 公式分解为:

e…emmmmmm，写了两遍了。。。理解了就好，不要嫌啰嗦哈！

2.2 特征独立假设

这一部分参考别人的哦！
这一部分开始朴素贝叶斯的理论推导，从中你会深刻地理解什么是特征条件独立假设。
给定训练数据集 $(X,Y)$，其中每个样本 $X$ 都包括 $n$ 维特征，即 $X=(x_1,x_2,x_3,...,x_n)$，类标记集合含有$k$种类别，即 $Y=(y_1,y_2,...,y_k)$。
现在来了一个新样本 $x$，我们要怎么判断它的类别呢？从概率的角度来看，这个问题就是给定 $x$，它属于哪个类别的概率最大。那么问题就转化为求解$P(y_1|x),P(y_2|x),...,P(y_k|x)$ 中最大的那个，即求后验概率最大的输出：$argMA{X}_{(}{y}_k)P(y_k|x)$。
那 $P(y_k|x)$ 怎么求解？答案就是贝叶斯定理：

根据全概率公式，可以进一步地分解上式中的分母：

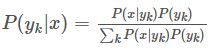
上式分子中的$P(y_k)$是先验概率，根据训练集就可以简单地计算出来。
而条件概率$P(x|y_k)=P(x_1,x_2,...,x_n|y_k)$，它的参数规模是指数数量级别的，假设第 $i$ 维特征 $x_i$ 可取值的个数有$S_i$个，类别取值个数为 $k$ 个，那么参数个数为：$k(S_1\ast S_2\ast ....\ast S_n)$.这显然不可行。针对这个问题，朴素贝叶斯算法对条件概率分布作出了独立性的假设，通俗地讲就是说假设各个维度的特征 $x_1,x_2,...,x_n$ 互相独立，在这个假设的前提上，条件概率可以转化为：
$P(x|y_k)=P(x_1,x_2,...,x_n|y_k)=P(x_1|y_k)\ast P(x_2|y_k)\ast P(x_3|y_k)\ast ...P(x_n|y_k)。参数个数下降为k(S_1+S_2+...+S_N)$。
以上就是针对条件概率所作出的特征条件独立性假设，至此，先验概率$P(y_k)$和条件概率$P(x|y_k)$的求解问题就都解决了，那么我们是不是可以求解我们所要的后验概率$P(y_k|x)$了？当然OK~~啦！将上式公式带入，可得：

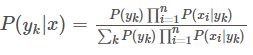
于是朴素贝叶斯分类器可表示为：

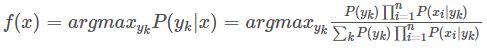
因为对所有的$y_k$，上式中的分母的值都是一样的（为什么？注意到全加符号就容易理解了），所以可以忽略分母部分，朴素贝叶斯分类器最终表示为：

关于$P(y_k)，P(x_i|y_k)$的求解，有以下三种常见的模型。

---

3、求解的三种模型

求解$P(y_k)，P(x_i|y_k)$的三种模型：多项式模型、高斯模型、伯努利模型。

3.1 多项式模型

该模型常用于文本分类，特征是单词，值是单词的出现次数。
其中，$N{y}_k{x}_i$是类别$y_k$下特征$x_i$出现的总次数；$N{y}_k$是类别$y_k$下所有特征出现的总次数。对应到文本分类里，如果单词$word$在一篇分类为$label1$的文档中出现了5次，那么$N_{(}label1,word)$的值会增加5。如果是去除了重复单词的，那么$N(label1,word)$的值会增加1。$n$是特征的数量，在文本分类中就是去重后的所有单词的数量。$\alpha$的取值范围是[0,1]，比较常见的是取值为1。
待预测样本中的特征$x_i$在训练时可能没有出现，如果没有出现，则$N{y}_k{x}_i$值为0，如果直接拿来计算该样本属于某个分类的概率，结果都将是0。在分子中加入$\alpha$，在分母中加入$\alpha n$可以解决这个问题。也可以使用$Laplace$校准，思想差不多。

---

3.2 高斯模型

有些特征可能是连续型变量，比如说人的身高，物体的长度，这些特征可以转换成离散型的值，比如如果身高在160cm以下，特征值为1；在160cm和170cm之间，特征值为2；在170cm之上，特征值为3。也可以这样转换，将身高转换为3个特征，分别是$f_1、f_2、f_3$，如果身高是160cm以下，这三个特征的值分别是1、0、0，若身高在170cm之上，这三个特征的值分别是0、0、1。不过这些方式都不够细腻，高斯模型可以解决这个问题。高斯模型假设这些一个特征的所有属于某个类别的观测值符合高斯分布，也就是：

---

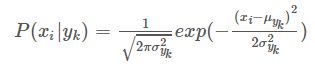
3.3 伯努利模型

伯努利模型中，对于一个样本来说，其特征用的是全局的特征。
在伯努利模型中，每个特征的取值是布尔型的，即 $true$和$false$，或者1和0。例如在文本分类中，就是一个特征有没有在一个文档中出现。
如果特征值$x_i$值为1,那么

如果特征值$x_i$值为0,那么

这意味着，“没有某个特征”也是一个特征。

e…emmmmmm，这上面写的挺抽象的模型。。。写代码时候理解就可以啦！

---

4、朴素贝叶斯算法流程

首先根据给定的训练样本求先验概率和条件概率，也就是上文求的那两个式子，然后训练计数后给定一个样本，计算在不同类别下该样本出现的概率，求得最大值即可。

---

5、代码块

代码块语法遵循标准markdown代码，例如：

# coding=utf-8
# Author:Dodo
# Date:2018-11-17
# Email:[email protected]

'''
数据集：Mnist
训练集数量：60000
测试集数量：10000
------------------------------
运行结果：
    正确率：84.3%
    运行时长：74s
'''

import numpy as np
import time

def loadData(fileName):
    '''
    加载文件
    :param fileName:要加载的文件路径
    :return: 数据集和标签集
    '''
    #存放数据及标记
    dataArr = []
    labelArr = []
    #读取文件
    fr = open(fileName)
    #遍历文件中的每一行
    for line in fr.readlines():
        #获取当前行，并按“，”切割成字段放入列表中
        #strip：去掉每行字符串首尾指定的字符（默认空格或换行符）
        #split：按照指定的字符将字符串切割成每个字段，返回列表形式
        curLine = line.strip().split(',')
        #将每行中除标记外的数据放入数据集中（curLine[0]为标记信息）
        #在放入的同时将原先字符串形式的数据转换为整型
        #此外将数据进行了二值化处理，大于128的转换成1，小于的转换成0，方便后续计算
        dataArr.append([int(int(num) > 128) for num in curLine[1:]])
        #将标记信息放入标记集中
        #放入的同时将标记转换为整型
        labelArr.append(int(curLine[0]))
    #返回数据集和标记
    return dataArr, labelArr

def NaiveBayes(Py, Px_y, x):
    '''
    通过朴素贝叶斯进行概率估计
    :param Py: 先验概率分布
    :param Px_y: 条件概率分布
    :param x: 要估计的样本x
    :return: 返回所有label的估计概率
    '''
    #设置特征数目
    featrueNum = 784
    #设置类别数目
    classNum = 10
    #建立存放所有标记的估计概率数组
    P = [0] * classNum
    #对于每一个类别，单独估计其概率
    for i in range(classNum):
        #初始化sum为0，sum为求和项。
        #在训练过程中对概率进行了log处理，所以这里原先应当是连乘所有概率，最后比较哪个概率最大
        #但是当使用log处理时，连乘变成了累加，所以使用sum
        sum = 0
        #获取每一个条件概率值，进行累加
        for j in range(featrueNum):
            sum += Px_y[i][j][x[j]]
        #最后再和先验概率相加（也就是式4.7中的先验概率乘以后头那些东西，乘法因为log全变成了加法）
        P[i] = sum + Py[i]

    #max(P)：找到概率最大值
    #P.index(max(P))：找到该概率最大值对应的所有（索引值和标签值相等）
    return P.index(max(P))


def test(Py, Px_y, testDataArr, testLabelArr):
    '''
    对测试集进行测试
    :param Py: 先验概率分布
    :param Px_y: 条件概率分布
    :param testDataArr: 测试集数据
    :param testLabelArr: 测试集标记
    :return: 准确率
    '''
    #错误值计数
    errorCnt = 0
    #循环遍历测试集中的每一个样本
    for i in range(len(testDataArr)):
        #获取预测值
        presict = NaiveBayes(Py, Px_y, testDataArr[i])
        #与答案进行比较
        if presict != testLabelArr[i]:
            #若错误  错误值计数加1
            errorCnt += 1
    #返回准确率
    return 1 - (errorCnt / len(testDataArr))


def getAllProbability(trainDataArr, trainLabelArr):
    '''
    通过训练集计算先验概率分布和条件概率分布
    :param trainDataArr: 训练数据集
    :param trainLabelArr: 训练标记集
    :return: 先验概率分布和条件概率分布
    '''
    #设置样本特诊数目，数据集中手写图片为28*28，转换为向量是784维。
    # （我们的数据集已经从图像转换成784维的形式了，CSV格式内就是）
    featureNum = 784
    #设置类别数目，0-9共十个类别
    classNum = 10

    #初始化先验概率分布存放数组，后续计算得到的P(Y = 0)放在Py[0]中，以此类推
    #数据长度为10行1列
    Py = np.zeros((classNum, 1))  # shape(10,1)
    #对每个类别进行一次循环，分别计算它们的先验概率分布
    #计算公式为书中"4.2节 朴素贝叶斯法的参数估计 公式4.8"
    for i in range(classNum):
        #下方式子拆开分析
        #np.mat(trainLabelArr) == i：将标签转换为矩阵形式，里面的每一位与i比较，若相等，该位变为Ture，反之False
        #np.sum(np.mat(trainLabelArr) == i):计算上一步得到的矩阵中Ture的个数，进行求和(直观上就是找所有label中有多少个
        #为i的标记，求得4.8式P（Y = Ck）中的分子)
        #np.sum(np.mat(trainLabelArr) == i)) + 1：参考“4.2.3节 贝叶斯估计”，例如若数据集总不存在y=1的标记，也就是说
        #手写数据集中没有1这张图，那么如果不加1，由于没有y=1，所以分子就会变成0，那么在最后求后验概率时这一项就变成了0，再
        #和条件概率乘，结果同样为0，不允许存在这种情况，所以分子加1，分母加上K（K为标签可取的值数量，这里有10个数，取值为10）
        #参考公式4.11
        #(len(trainLabelArr) + 10)：标签集的总长度+10.
        #((np.sum(np.mat(trainLabelArr) == i)) + 1) / (len(trainLabelArr) + 10)：最后求得的先验概率
        Py[i] = ((np.sum(np.mat(trainLabelArr) == i)) + 1) / (len(trainLabelArr) + 10)
    #转换为log对数形式
    #log书中没有写到，但是实际中需要考虑到，原因是这样：
    #最后求后验概率估计的时候，形式是各项的相乘（“4.1 朴素贝叶斯法的学习” 式4.7），这里存在两个问题：1.某一项为0时，结果为0.
    #这个问题通过分子和分母加上一个相应的数可以排除，前面已经做好了处理。2.如果特诊特别多（例如在这里，需要连乘的项目有784个特征
    #加一个先验概率分布一共795项相乘，所有数都是0-1之间，结果一定是一个很小的接近0的数。）理论上可以通过结果的大小值判断， 但在
    #程序运行中很可能会向下溢出无法比较，因为值太小了。所以人为把值进行log处理。log在定义域内是一个递增函数，也就是说log（x）中，
    #x越大，log也就越大，单调性和原数据保持一致。所以加上log对结果没有影响。此外连乘项通过log以后，可以变成各项累加，简化了计算。
    #在似然函数中通常会使用log的方式进行处理（至于此书中为什么没涉及，我也不知道）
    Py = np.log(Py)

    #计算条件概率 Px_y=P（X=x|Y = y）
    #计算条件概率分成了两个步骤，下方第一个大for循环用于累加，参考书中“4.2.3 贝叶斯估计 式4.10”，下方第一个大for循环内部是
    #用于计算式4.10的分子，至于分子的+1以及分母的计算在下方第二个大For内
    #初始化为全0矩阵，用于存放所有情况下的条件概率
    Px_y = np.zeros((classNum, featureNum, 2))  # shape(10,784,2)
    #对标记集进行遍历
    for i in range(len(trainLabelArr)):
        #获取当前循环所使用的标记
        label = trainLabelArr[i]
        #获取当前要处理的样本
        x = trainDataArr[i]
        #对该样本的每一维特诊进行遍历
        for j in range(featureNum):
            #在矩阵中对应位置加1
            #这里还没有计算条件概率，先把所有数累加，全加完以后，在后续步骤中再求对应的条件概率
            Px_y[label][j][x[j]] += 1


    #第二个大for，计算式4.10的分母，以及分子和分母之间的除法
    #循环每一个标记（共10个）
    for label in range(classNum):
        #循环每一个标记对应的每一个特征
        for j in range(featureNum):
            #获取y=label，第j个特诊为0的个数
            Px_y0 = Px_y[label][j][0]
            #获取y=label，第j个特诊为1的个数
            Px_y1 = Px_y[label][j][1]
            #对式4.10的分子和分母进行相除，再除之前依据贝叶斯估计，分母需要加上2（为每个特征可取值个数）
            #分别计算对于y= label，x第j个特征为0和1的条件概率分布
            Px_y[label][j][0] = np.log((Px_y0 + 1) / (Px_y0 + Px_y1 + 2))
            Px_y[label][j][1] = np.log((Px_y1 + 1) / (Px_y0 + Px_y1 + 2))

    #返回先验概率分布和条件概率分布
    return Py, Px_y


if __name__ == "__main__":
    start = time.time()
    # 获取训练集
    print('start read transSet')
    trainDataArr, trainLabelArr = loadData('../Mnist/mnist_train.csv')

    # 获取测试集
    print('start read testSet')
    testDataArr, testLabelArr = loadData('../Mnist/mnist_test.csv')

    #开始训练，学习先验概率分布和条件概率分布
    print('start to train')
    Py, Px_y = getAllProbability(trainDataArr, trainLabelArr)

    #使用习得的先验概率分布和条件概率分布对测试集进行测试
    print('start to test')
    accuracy = test(Py, Px_y, testDataArr, testLabelArr)

    #打印准确率
    print('the accuracy is:', accuracy)
    #打印时间
    print('time span:', time.time() -start)