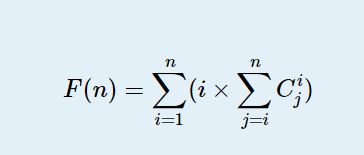“字节跳动-文远知行杯”广东工业大学第十四届程序设计竞赛 1,2,3,4,5,7,8,9,10
1001:
hzy 和zsl 的生存挑战
Problem Description
zsl 和hzy 来到了臭臭城堡,打算挑战臭臭城堡的大魔王hyz,大魔王hyz设置了这样的一个挑战:
- zsl 和hzy两个人各自来到一间密室,期间两人无法以任何形式交流
- 大魔王hyz会随机在两个人的脑海里各发送一个数字,0或者是1
- zsl 和 hzy 需要猜对这俩个数字才算通关,但是大魔王hyz觉得人生不能过于无敌,因此降低难度,只要两个人中有一个人答对就算是通关
现在大魔王hyz 给出的数字可能的情况有 00, 01, 10, 11 四种,请按上述枚举的顺序,计算所有情况下zsl 和hzy 通关的几率。(假设zsl 和 hzy 两个人都足够机智,能够选择出最优决策)
Input
(空)
Output
输出四个答案,每个答案后面跟随一个换行符并且保留两位小数位,分别对应00,01,10,11的情况下,zsl和hzy通关的几率
Sample Input
(空)
Sample Output
1.00
0.00
0.50
0.55 (输出仅做格式参考,不保证正确性)
题意:
给你什么都没给你。。
问有两个人,他们每个人得到了0或者1一个数字,他们任意一个人猜出两个数字即可过关,问你如果分别给每个人0 0,0 1,1 0,1 1,他们通关的几率。
题解:
???什么玩意,我也是wa了一发觉得这是个文字游戏,他题目里说(假设zsl 和 hzy 两个人都足够机智,能够选择出最优决策),那他们这么机智怎么不是全对呢?然后就试了4个1,A了。。。
#include
using namespace std;
int main()
{
for(int i=1;i<=4;i++)
printf("1.00\n");
return 0;
}
1002:
人类史上最大最好的希望事件
Problem Description
作为CNCS的半壁江山,狗哥常常在宇宙中心邵阳眺望黄浦江,夜晚的星空总是迷人,有时候还能见到彗星滑落。
狗哥是幸运的,他在两秒钟内看到了十七颗彗星划过天际,作为打ACM的学者,自然不会有「稳定-1」情况。他开始研究彗星运动的轨迹,发现他们都遵照斐波那契螺旋线在运动着。
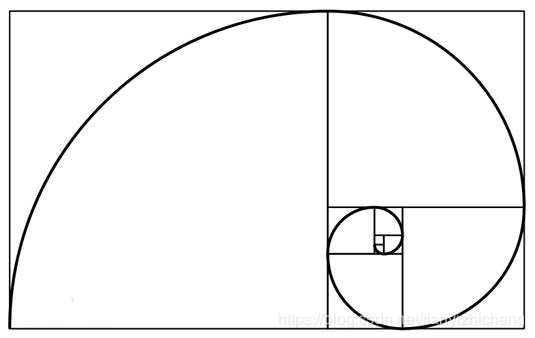
尤里卡!狗哥觉得这就是找寻「生命,宇宙和一切的终极答案」的精要所在,但是怎么表示呢?狗哥觉得求取斐波那契螺旋线经过的一个个方格的面积之和就是公式的表现。
例如下图,螺旋线每划过一个方格,都转过了四分之一圈。如果我们以四分之一圈为单位,那么我们用类似带分数的形式表示螺旋线转动的起点和终点。例如,0+0 到 0 + 1 意即从第一个方格转到第二个方格,划过了前两个方格,他们的面积之和为2(1+1)。同理,0+0 到 1+0 划过了前五个方格,他们的面积之和为40(1+1+4+9+25)。
但是聪明的狗哥需要一个程序去获得指定范围内的螺旋线面积之和,狗哥给了你一首「希望之花」的时间,而他需要利用这个时间去打出四暗刻单骑。如果你能完成这个程序,狗哥会封你为格拉摩根伯爵
Input
不定组数据。
首先输入一个整数Q,代表狗哥询问次数。
接下来Q行,每行四个整数a,b,c,d,代表狗哥想求 a+b 到 c+d 之间的螺旋线面积之和。
1<= Q <= 10000
0<= a,c <= 10000
0 <= b,d <= 3
结果对192600817取模。
Output
一个数字,表示螺旋线面积之和。
Sample Input
4
0 0 0 1
0 0 1 0
1 2 2 1
1 1 0 3
4
0 0 0 1
0 0 1 0
1 2 2 1
1 1 0 3
Sample Output
2
40
4791
98
2
40
4791
98
题意:
一个斐波那契数相当于一个1/4圆,一个图形的面积是这个斐波那契数的平方,给你a,b,c,d的意思是a又b/4个圆到c又d/4个圆的面积是多少。
题解:
没有什么难度,直接预处理就好了,把a当做4a,c当做4c,但是c也有可能比a小。
#include
using namespace std;
#define ll long long
ll mod=192600817;
ll m[50005],fac[50005];
void init()
{
fac[0]=fac[1]=1;
m[0]=1,m[1]=2;
for(int i=2;i<50005;i++)
{
fac[i]=fac[i-1]+fac[i-2];
m[i]=(m[i-1]+(fac[i]%mod)*fac[i])%mod;
fac[i]%=mod;
}
}
int main()
{
init();
int t;
while(~scanf("%d",&t))
{
while(t--)
{
int a,b,c,d;
scanf("%d%d%d%d",&a,&b,&c,&d);
if(min(4*c+d,4*a+b)==0)
printf("%lld\n",m[max(4*c+d,4*a+b)]);
else
printf("%lld\n",(m[max(4*c+d,4*a+b)]-m[min(4*c+d,4*a+b)-1]+mod)%mod);
}
}
return 0;
}
1003:
超级无敌简单题
Problem Description
通常来说,题面短的题目一般都比较难,所以我要把题面写得很长很长。
通常来说,题面短的题目一般都比较难,所以我要把题面写得很长很长。
通常来说,题面短的题目一般都比较难,所以我要把题面写得很长很长。
鸽子数字由以下过程定义:从任何正整数开始,将数字替换为其各个数位的平方和,并重复该过程,直到该数字等于1。如果不能,则这个数字不是鸽子数。
例如7是鸽子数,因为7->49->97->130->10->1。(77=49,44+99=97,99+7*7=130…如此类推)
显然1是第一个鸽子数。
有Q个询问,每个询问给出一个数k,你需要输出第k个鸽子数。
Input
第一行一个Q,代表询问的个数(Q<=100000)
接下来Q行,每行一个数字k(k<150000)
Output
每行输出一个数,代表第k个鸽子数
Sample Input
2
1
2
Sample Output
1
7
题意:很短自己看吧
题解:
以前做过一道类似的题目,当时记得出现4的就是不能的,然后我在打表的时候发现这种数其实还是蛮多的,然后就直接找到前面15e4个就Ac了。
#include
using namespace std;
#define ll long long
int ans[200005];
int main()
{
int s=0;
for(ll n=1;s<=150000;n++)
{
ll x=n;
ll sum=0,cnt=1;
while(cnt<=100)
{
while(x)
sum+=(x%10)*(x%10),x/=10;
x=sum,sum=0;
if(x==1||x==4||x>1e9)
break;
cnt++;
}
if(x==1)
ans[++s]=n;
}
int t;
scanf("%d",&t);
while(t--)
{
int n;
scanf("%d",&n);
printf("%d\n",ans[n]);
}
return 0;
}
1004:
免费送气球
Problem Description
又到了GDUT一年一度的程序设计竞赛校赛的时间啦。同学们只要参加校赛,并且每解出一道题目就可以免费获得由ACM协会和集训队送出的气球一个。听到这个消息,JMC也想参加免费拿气球。可是,由于JMC太菜了而被禁止参赛,于是他找到你想让你帮忙参加比赛,可以通过执行下面的C++程序解决问题后获得气球并送给他。JMC保证了下面的程序一定能获得正确的结果。
void solve(int Q, int type[], long long first[], long long second[]) {
vector vec;
for (int i = 0; i < Q; ++i) {
if (type[i] == 1) {
long long k = first[i], val = second[i];
while (k–) {
vec.push_back(val);
}
}
else if (type[i] == 2) {
sort(vec.begin(), vec.end());
long long l = first[i] - 1, r = second[i], res = 0;
while (l < r) {
res = (res + vec[l++]) % 1000000007;
}
printf("%lld\n", res);
}
}
}
为防止你被JMC的代码搞到头晕目眩,JMC特意给出了问题的文字描述。已知一开始有一个空序列,接下来有Q次操作,每次操作给出type、first和second三个值。当type为1时,意味着该操作属于第一种操作:往序列尾部添加first个second数。当type为2时,意味着该操作属于第二种操作:查询序列中第first小至第second小的数值之和(一共有(second - first + 1)个数被累加),并将结果对1000000007取模后输出。
Input
单组数据
第一行一个Q(1 <= Q <= 1e5),代表Q次操作。
接下来有Q行,每行包含三个整数type、first和second;其中1 <= type <= 2。当type等于1时,0 <= first,second < 1e9。当type等于2时,1 <= first <= second,且first和second均不大于目前已添加进序列的数的数量。
Output
对于每次操作二,将结果对1000000007取模后输出。
Sample Input
6
1 5 1
1 6 3
2 2 5
2 4 8
1 2 2
2 4 8
Sample Output
4
11
9
题意:
给你n个操作,有两种操作,1 x y表示你得到了x个y,2 x y表示输出在你得到的这些数中,第x小到第y小的数的和是多少。
题解:
一看就是主席树,但是只剩40分钟了,不敢写,那就改成权值线段树,num表示这里有几个数,sum表示这里的数的和是多少,注意num不能取模。首先它的数据范围是1e5,那么我们就可以离散化,之后把1放到位置为1的地方,2放到位置为2的地方。那么就是单点更新,区间查询的话,如果直接查询这个区间感觉很麻烦,我就查询r的前缀-l的前缀+mod%mod。
#include
using namespace std;
const int N=1e5+5;
#define ll long long
ll mod=1e9+7;
struct que
{
int op;
ll x,y;
}q[N];
ll a[N];
ll num[N*4],sum[N*4];
void pushup(int root)
{
num[root]=num[root<<1]+num[root<<1|1];
sum[root]=(sum[root<<1]+sum[root<<1|1])%mod;
}
void update(int l,int r,int root,ll n,ll pos)
{
if(l==r)
{
num[root]+=n;
(sum[root]+=a[pos]*n)%=mod;
return ;
}
int mid=l+r>>1;
if(mid>=pos)
update(l,mid,root<<1,n,pos);
else
update(mid+1,r,root<<1|1,n,pos);
pushup(root);
}
ll query(int l,int r,int root,ll n)
{
if(n==0)
return 0;
if(l==r)
return n*a[l]%mod;
int mid=l+r>>1;
if(num[root<<1]<=n)
return (sum[root<<1]+query(mid+1,r,root<<1|1,n-num[root<<1]))%mod;
else
return query(l,mid,root<<1,n);
}
int main()
{
int n,all=0;
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%d%lld%lld",&q[i].op,&q[i].x,&q[i].y);
if(q[i].op==1)
a[++all]=q[i].y;
}
sort(a+1,a+1+all);
all=unique(a+1,a+1+all)-a-1;
for(int i=1;i<=n;i++)
{
if(q[i].op==1)
{
q[i].y=lower_bound(a+1,a+1+all,q[i].y)-a;
update(1,all,1,q[i].x,q[i].y);
}
else
{
printf("%lld\n",(query(1,all,1,q[i].y)-(q[i].x==1?0:query(1,all,1,q[i].x-1))+mod)%mod);
}
}
return 0;
}
1005:
水题
Problem Description
cj最近沉浸在线性代数的世界里不能自拔,今天又发现一条有趣的问题了。平面中有一个三角形,三个顶点是(0,0),(1,0),(0,1),经过某种变换后三个顶点分别到了(2,2),(0,2),(2,0),则原本的(1,1)点到了哪?聪明的 cj 一眼就看出了是在(0,0),此处掌声应用十万伏特!下面的变换也实在是太过简单,因为每次所取的三个点不会共线,且 x 坐标都不同,且非零,实在太简单了,于是他决定把问题交给你
现给出一对三角形变换前后的坐标,请你算出其他点变换后的坐标
Input
第一行 1 个数,代表 T 组样例
下面每组样例:
第一行 6 个数,代表变换前的三个点 x1,y1,x2,y2,x3,y3
第二行 6 个数,代表变换后的三个点 x4,y4,x5,t5,x6,y6
第三行 1 个数,代表询问的个数 Q(Q<=1000000)
接下来 Q 行,每行两个整数,x,y(范围[-1000,+1000])
Output
x,y 变换后的坐标,每个值两位小数
Sample Input
1
2 1 3 2 1 2
3 1 5 2 2 3
1
2 3
Sample Output
4.00 4.00
题意:
给你一个三角形的初始位置和变换之后的位置,问你原来空间上的某个点经过这样的变换之后变成哪个点了。
题解:
确实不会这种题目,还是赛后问别人才知道是一道水题的,我们先求出刚开始的后面两个点对于第一个点的向量,在求出变换之后后面两个点对于第一个点的向量,这是个线性变换,那么12的矩阵要得到12的矩阵,只有乘上2*2的矩阵,求出这个矩阵之后,对于每个给你的点,先求出它关于三角形第一个点变换之前的向量,乘上这个矩阵得到变换之后的向量,再加上三角形第一个点变换之后的坐标即可。
#include
using namespace std;
int main()
{
double x[10],y[10];
int t;
scanf("%d",&t);
while(t--)
{
for(int i=1;i<=6;i++)
scanf("%lf%lf",&x[i],&y[i]);
double a,b,c,d;
for(int i=2;i<=3;i++)
x[i]-=x[1],y[i]-=y[1];
for(int i=5;i<=6;i++)
x[i]-=x[4],y[i]-=y[4];
c=(x[5]*x[3]-x[6]*x[2])/(y[2]*x[3]-x[2]*y[3]);
a=(x[5]-y[2]*c)/x[2];
d=(y[5]*x[3]-y[6]*x[2])/(y[2]*x[3]-x[2]*y[3]);
b=(y[5]-y[2]*d)/x[2];
int q;
scanf("%d",&q);
while(q--)
{
scanf("%lf%lf",&x[2],&y[2]);
x[2]-=x[1],y[2]-=y[1];
printf("%.2f %.2f\n",x[2]*a+y[2]*c+x[4],x[2]*b+y[2]*d+y[4]);
}
}
return 0;
}
1007:
简单数学题
Problem Description
已知
求 F(n) mod 1000000007
Input
多组输入,每组输入占一行,包含一个整数n(1 <= n <= 1e18)。
数据不超过300000组。
Output
对于每组输入,输出一行,包括一个数代表答案。
Sample Input
5
100
Sample Output
129
660756544
题意:如图
题解:打表
发现每个数是 ( i − 1 ) ∗ 2 i + 1 (i-1)*2^i+1 (i−1)∗2i+1。
注意快速幂的时候,,n不能取模
#include
using namespace std;
#define ll long long
ll mod=1e9+7;
ll qpow(ll a,ll b)
{
ll ret=a,ans=1;
while(b)
{
if(b&1)
ans=ans*ret%mod;
ret=ret*ret%mod;
b/=2ll;
}
return ans;
}
int main()
{
ll n;
while(~scanf("%lld",&n))
{
printf("%lld\n",((n-1)%mod*qpow(2ll,n)+1)%mod);
}
return 0;
}
1008:
zyb的面试
Problem Description
今天zyb参加一场面试,面试官听说zyb是ACMer之后立马抛出了一道算法题给zyb:
有一个序列,是1到n的一种排列,排列的顺序是字典序小的在前,那么第k个数字是什么?
例如n=15,k=7, 排列顺序为1, 10, 11, 12, 13, 14, 15, 2, 3, 4, 5, 6, 7, 8, 9;那么第7个数字就是15.
那么,如果你处在zyb的场景下,你能解决这个问题吗?
Input
T组样例(T<=100)
两个整数n和k(1<=n<=1e6,1<=k<=n),n和k代表的含义如上文
Output
输出1-n之中字典序第k小的数字
Sample Input
1
15 7
Sample Output
15
题意:很短
题解:
这道题好像在哪里做到过?cf吗还是什么。我们可以发现这就是个十叉树,每次只需要找比当前大的十倍的数有多少,够不够k,比如说15 7,那么在1的时候,1的儿子有6个数,发现加起来正好与k相同,那么就说明需要的数在这些数里面,继续往下,发现10的儿子只有一个,那么就变成11,以此类推。
#include
using namespace std;
int getSteps(int n, long n1, long n2) {
int steps = 0;
while (n1 <= n) {
steps += min((long )n + 1, n2) - n1;
n1 *= 10;
n2 *= 10;
}
return steps;
}
int findKthNumber(int n, int k) {
int cur = 1;
while (k!=1) {
int steps = getSteps(n, cur, cur + 1);
if (steps < k) {
cur += 1;
k -= steps;
} else {
cur *= 10;
k -= 1;
}
}
return cur;
}
int main()
{
int t;
scanf("%d",&t);
while(t--)
{
int n,k;
scanf("%d%d",&n,&k);
printf("%d\n",findKthNumber(n,k));
}
return 0;
}
1008:
故事
Problem Description
这是一个极其老套的故事,无论怎样的描述都会因为故事本身的古老而显得陈词滥调。这个故事究竟有多古老呢?你需要调用你的一切想象力,沿着时间线回溯,穿过麦田,穿过绿林,穿过那铺着大理石的长廊,来到那金碧辉煌的宫殿大堂前,来到那体态臃肿的国王面前。你将看见那神情激动的国王,将手一挥,只留下回荡在肃穆的大堂里的一句话――“去吧!消灭恶龙!拯救公主!”。
好吧,其实这就是一个勇士为拯救公主踏上讨伐恶龙的征程的故事。勇士名叫wdh,此刻他正在恶魔森林里和分裂怪搏斗刷经验呢。
可恶的分裂怪最大的特征就是会分裂,但是它并不是无限分裂的。分裂怪有1到n种等级,第1级的分裂怪称为原子怪,它不会分裂,被击杀时会产生a[1]点经验;而第k级的分裂怪死亡时则会分裂成a[k]个第k - 1级的分裂怪。
wdh的闪躲和攻击技能已经满点了(wdh不会受到攻击),但是体力有限。他每次只能攻击一只分裂怪,攻击将消耗1点体力,且该分裂怪必死。
现在wdh遇到一个第N级的分裂怪,他想知道在现有体力下最多能获得多少经验,但是他正忙着应付怪物呢,所以想请你帮帮他。
Input
第一行包含N和Q,表示有N种等级的分裂怪和Q个询问(1 <= N <= 1e5, 1 <= Q <= 1e5)。
第二行包含N个整数,第i个整数表示上文意义的a[i]。(1 <= a[i] <= 1e9)
第三行包含Q个整数,每个整数w表示wdh的体力值。(0 <= w <= 1e9)
Output
输出Q行,每行一个整数,表示在当前体力下wdh最多能获得多少经验。
Sample Input
3 3
2 2 2
5 7 8
Sample Output
4
8
8
题意:
给你一棵树,问你从顶端走到底端,你最多能走q个点,问你能走到最多多少叶子结点
题解:
由于它满足二分的性质,所以可以二分,我们二分可以走到的叶子结点有多少个,然后从下往上除上一个节点的儿子个数,这样就可以知道上一个节点有多少个,如果每个节点的儿子数都大于2的话,那么复杂度就是O(nlognlogn),但是有可能有儿子数为1的节点,那么我们就把它压缩到儿子节点上,就当做走一步要消耗两个就可以了,对于已经枚举到1条链的话,我们就可以直接减去从当前到根节点会经过多少个节点,看看是否大于等于0就ok了。
#include
using namespace std;
#define ll long long
const int N=1e5+5;
int all;
ll son[N],val[N];
int n,q;
int check(ll mid,ll x)
{
int sum=n;
for(int i=1;i<=all;i++)
{
if(mid==1)
return (x-sum)>=0;
sum-=val[i];
x-=mid*val[i];
if(i=low)
{
mid=low+high>>1;
if(check(mid,x))
low=mid+1,ans=mid;
else
high=mid-1;
}
printf("%lld\n",ans*son[1]);
}
return 0;
}
1009:
Count——矩阵快速幂
Problem Description
Farmer John有n头奶牛.
某天奶牛想要数一数有多少头奶牛,以一种特殊的方式:
第一头奶牛为1号,第二头奶牛为2号,第三头奶牛之后,假如当前奶牛是第n头,那么他的编号就是2倍的第n-2头奶牛的编号加上第n-1头奶牛的编号再加上自己当前的n的三次方为自己的编号.
现在Farmer John想知道,第n头奶牛的编号是多少,估计答案会很大,你只要输出答案对于123456789取模.
Input
第一行输入一个T,表示有T组样例
接下来T行,每行有一个正整数n,表示有n头奶牛 (n>=3)
其中, T = 1 0 4 , n < = 1 0 18 T=10^4,n<=10^{18} T=104,n<=1018
Output
共T行,每行一个正整数表示所求的答案
Sample Input
5
3
6
9
12
15
Sample Output
31
700
7486
64651
527023
题意:
f[i]=2f[i-2]+f[i-1]+ii*i,给你n,输出f[n]
题解:
以前有一道很像的题目来着里面一共有5个变量f[i-1],f[i-2],i,i,i,那么需要一个6*6的矩阵
1 2 1 0 0 0 0 f[i-1] f[i]
1 0 0 0 0 0 0 f[i-2] f[i-1]
0 0 0 1 3 3 1 i^3 (i+1)^3
0 0 0 0 1 2 1 i^2 (i+1)^2
0 0 0 0 0 1 1 i i+1
0 0 0 0 0 0 1 1 1
之后矩阵快速幂就ok拉
#include
using namespace std;
typedef long long ll;
const ll mod=123456789,maxn=6;
struct Matrix
{
ll m[maxn][maxn];
Matrix()
{
memset(m,0,sizeof(m));
}
void init()
{
for(int i=0; i>=1;
}
return ans;
}
};
int main()
{
int t;
ll n,m,a,b;
scanf("%d",&t);
while(t--)
{
scanf("%lld",&n);
if(n==1)
{
cout<<1<